道长的算法笔记:生成树问模型
(一)生成树
阅读之前,需要掌握贪心算法、并查集、图数据结构存储的前置知识,否则读起来会很吃力。通俗来说,生成树是指从一个图中提取一个树结构,最小生成树是指边权总和最小的生成树。本节我们需要讨论最小生成树、次小生成树等变体问题,当然有些时候我们要算的也有可能是最大生成树生成树,相关算法的综述参考 OI-Wiki,下列简单给出代码。
(1.1) Prim算法
Prim 算法代码看起来非常像是 Dijstra,因为二者都是基于贪心思想实现,但是二者的松弛方程,以及 \(dist\) 数组含义不相同,我们不妨把当前已经构造的生成树记作 \(T\), Prim 算法的 \(dist[i]\) 数组是指顶点 \(i\) 到达当前生成树 \(T\) 距离。
起始的时候 \(T=\empty\),我们首先先找一个起点 \(src\),并将 \(dist[src] = 0\),其余顶点 \(dist\) 全部设为无穷大。接着,我们再从所有顶点中找出一个距离 \(T\) 最短的顶点,将其纳入当前 \(T\),用于更新边权和,显然第一轮中,这个被找出来的顶点就是 \(src\),我们使用 \(src\) 更新与其邻接的顶点。
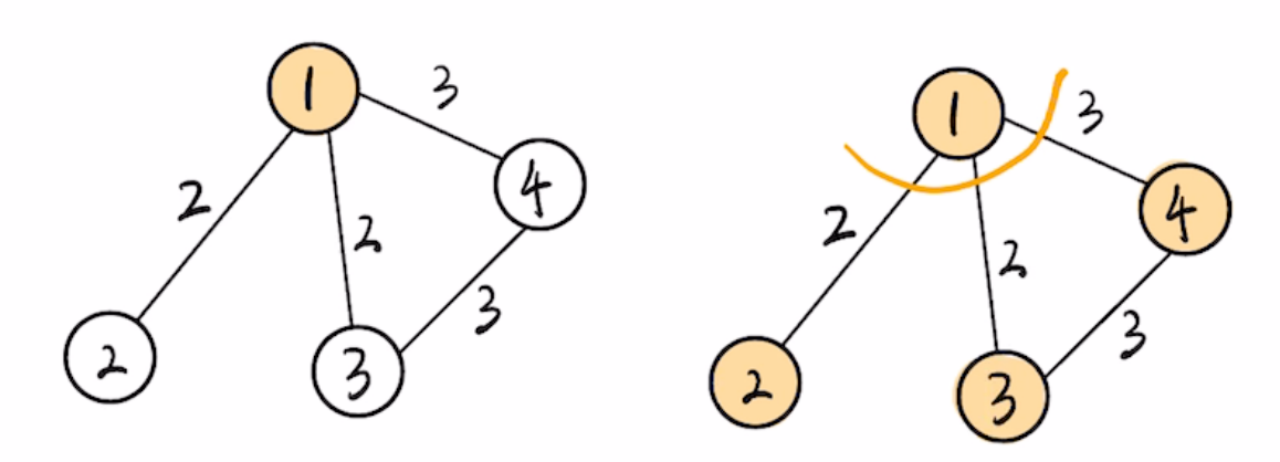
然后下一轮迭代中,我们再找一个未被访问,严格来说是未被加入生成树(使用 \(vist\) 标记),并且距离 \(T\) 最短的顶点,更新其邻接节点,如此重复,直接生成树 \(T\) 包换了原图所有节点。例如图中我们选择顶点 \(1\) 作为起点,第一轮循环中,我们会用 \(dist[1]\) 更新边权和,然后标记\(vist[1]\),更新其邻接节点 \(\{2,3,4\}\),第二轮中使用 \(dist[2]\) 更新边权和,标记 \(vist[2]\),由于没有邻接节点,接下来使用 \(dist[3]\) 更新边权,标记 \(vist[3]\) ,然后轮到顶点 \(dist[4]\) 更新边和,标记 \(vist[4]\)。顶点都已纳入生成树,算法执行结束。
void prim(int src){
int ans = 0;
memset(vist, 0, sizeof(vist));
memset(dist, 0x3f, sizeof(dist));
dist[src] = 0; // 起点纳入生成树,由于其在生成树内部故到生成树距离是零
for (int i = 0; i < n; i++){ // 每次仅能选出一个顶点,共有顶点 n,故应循环次数 n
int t = -1; // 每轮循环中找出当前距离 T 最近的顶点 (也即dist最小的顶点)
for (int j = 1; j <= n; j++){
if (!vist[j] && (t == -1 || dist[t] > dist[j])) {
t = j; // 并把游标移到顶点t,接下来使用 t 更新其邻边
}
}
// 判断是不是孤立节点,如果存在孤立节点则无法形成生成树
if(dist[t] == INF){
printf("orz\n");
return;
}
vist[t] = 1;
ans += dist[t]; // dist 代表顶点到达 T 距离,使用其更新边权和
for (int j = heads[t]; ~j; j = nxt[j]) { // 此时使用了链式前向星存图
int v = val[j], w = wgt[j];
if (!vist[v] && dist[v] > w){
dist[v] = w;
}
}
}
printf("%d\n", ans); // 返回最小生成树边权和
}
(1.2) Kruskal算法
Kruskal 算法理解起来非常简单,先把连边按照权值从小到大排序,然后遍历连边。假设最开始的时候每个顶点都是一个连通分量,我们要做的事情就是检查一下连边两个端点是否处在同一个连通分量,如果不在一个连通分量,合并一下。如果已经落在同一个连通分量则跳过,直至整张图只剩一个连通分量。
#include <bits/stdc++.h>
#include <limits>
using namespace std;
typedef long long LLong;
typedef unsigned long long ULL;
#define fi first
#define se second
#define MAXN 500005
typedef struct Edge{
int a, b, w;
} Edge;
Edge edges[MAXN];
int n, m, a, b, c, pt[MAXN];
int find(int x){
return (x != pt[x]) ? (pt[x] = find(pt[x])) : x;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d %d %d", &a, &b, &c);
edges[i] = {a, b, c};
}
for (int i = 1; i <= n; i++)
pt[i] = i;
sort(edges, edges + m, [](const Edge &a, const Edge &b){
return a.w < b.w;
});
int cnt = 0, ans = 0;
for (int i = 0; i < m; i++) {
int ar = find(edges[i].a), br = find(edges[i].b);
if(ar != br){
pt[ar] = pt[br];
ans += edges[i].w;
cnt++;
}
if (cnt == n - 1) break; // 如果已经连到只剩一个连通分量
}
if(cnt == n - 1){
printf("%d\n", ans);
}else {
printf("orz\n");
}
return 0;
}
(1.3) Boruvka算法
Boruvka 是最原始的最小生成树算法。能够套其它数据结构进行优化,个别场景中会优于 Prim 或 Kruskal,又或者有些场景可能会用到 Boruvka 思想,例如 牛客多校5670B,虽然这种情况比较少。
Boruvka 能被视为一个多路并进的 Prim,但它代码看起来像是糅合了Prim 或 Kruskal 算法一样,首先我们把每个顶点视为一个连通分量,使用 \(best\) 数组记录连接这个连通分量的 外部 最短边权值,然后遍历边集,使用连边的两个端点更新其所在连通分量相连的最短边,并且使用数组 \(pt\) 记录这条最短路指向的连通分量,如果使用 \(best\) 记录连接这个连通分量的最短边编号则无需另开一个 \(pt\) 数组,具体参考第二份代码实现。扫完一趟边集之后,再用这些最小边更新生成树并合并连通块,由于这些外部的最短边已被内化成为生成树的一部分,因而我们要在下一轮循环中,重置 \(best\) 数组,反复迭代,如果已经不再更新则跳出循环。
#include <bits/stdc++.h>
#include <limits>
using namespace std;
typedef pair<int, int> ii;
typedef tuple<int, int, int> iii;
#define lc(x) (x<<1)
#define rc(x) (x<<1|1)
#define fi first
#define se second
#define MAXN 500005
typedef struct Edge{
int a, b, w;
} Edge;
vector<Edge> edges;
int n, m, a, b, w, ft[MAXN], pt[MAXN], best[MAXN];
int find(int x) {
return x != ft[x] ? (ft[x] = find(ft[x])) : x;
}
int boruvka(){
int ans = 0, cnt = 0;
for (int i = 1; i <= n; i++)
ft[i] = i;
while (1) {
int no_update = 1;
memset(best, 0x3f, sizeof(best)); // 每轮循环都要记得把所有连通分量当前最小边设为无穷大
for (int i = 0; i < edges.size(); i++){ // 遍历边集合,使用连边的端点更新每个连通块连着的最小边
int ar = find(edges[i].a), br = find(edges[i].b), w = edges[i].w;
if(ar == br) continue;
if(w < best[ar]) best[ar] = w, pt[ar] = br;
if(w < best[br]) best[br] = w, pt[br] = ar;
// 这种做法存储最小连边的权值,由于丢失连边的编号,所以另外一个数组 pt,
// 数组 pt 记录这条连边用于连接哪两个连通分量, 如果 best 记录连边的编号也就不用另外开一个pt (point to) 数组了!
}
// 遍历顶点(其实是所有连通块),根据最小边合并连通块
for (int i = 1; i <= n; i++){
if (best[i] < INF && find(i) != find(pt[i])) {
cnt++;
ans += best[i], no_update = 0;
ft[find(i)] = ft[find(pt[i])];
}
}
if(no_update) break;
}
return cnt == n - 1 ? ans : -INF;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d %d %d", &a, &b, &w);
edges.push_back({a, b, w});
}
int t = boruvka();
if(t != -INF){
printf("%d\n", t);
}else{
printf("orz\n");
}
return 0;
}
上文我们提到了,如果使用 \(best\) 记录连接这个连通分量的最短边编号则无需另开一个 \(pt\) 数组,下面我们给出具体的代码实现,核心部分几乎太大变化,唯一需要留意的地方就是,在读其它人代码的时候,需要注意 \(best\) 数组含义。
#include <bits/stdc++.h>
#include <limits>
using namespace std;
typedef long long llong;
typedef unsigned long long ull;
#define fi first
#define se second
#define MAXN 500005
typedef struct Edge{
int a, b, w;
} Edge;
vector<Edge> edges;
/**
* 数组best记录了当前连通块与外部的最小连边
* 因而一旦合并了两个连通分类,与外部最小连边也就内化了,故每趟循环都要重置best数组
*/
int n, m, a, b, w, ft[MAXN], best[MAXN];
int find(int x) {
return x != ft[x] ? (ft[x] = find(ft[x])) : x;
}
// 使用best 记录连边的编号,而非最小连边的边权的
int boruvka(){
int ans = 0, cnt = 0;
for (int i = 1; i <= n; i++)
ft[i] = i;
while (1) {
// 每轮循环都要记得把所有连通分量当前最小边设为无穷大
int no_update = 1;
memset(best, -1, sizeof(best));
// 遍历边表集合(其实也能使用邻接表存储)使用连边的端点更新每个连通块连着的最小边
for (int i = 0; i < edges.size(); i++){
int ar = find(edges[i].a), br = find(edges[i].b), w = edges[i].w;
if(ar == br) continue;
if (best[ar] == -1 || w < edges[best[ar]].w) best[ar] = i;
if (best[br] == -1 || w < edges[best[br]].w) best[br] = i;
}
// 遍历所有连通块,根据最小边合并连通块
for (int i = 1; i <= n; i++){
if(best[i] == -1)
continue;
// 不添加这条判断, 下面edges数组访问会出现越界
int ar = find(edges[best[i]].a), br = find(edges[best[i]].b);
if (ar != br) {
ans += edges[best[i]].w;
ft[ar] = ft[br];
no_update = 0;
cnt++;
}
}
if(no_update) break;
}
return cnt == n - 1 ? ans : -INF;
}
int main() {
#ifdef _OJ_ONLINE_JUDGE_
freopen("../../in.txt","r",stdin);
freopen("../../out.txt","w",stdout);
#endif
scanf("%d %d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d %d %d", &a, &b, &w);
edges.push_back({a, b, w});
}
int t = boruvka();
if(t != -INF){
printf("%d\n", t);
}else{
printf("orz\n");
}
return 0;
}
(二)次小生成树
Waiting...
支持作者



 浙公网安备 33010602011771号
浙公网安备 33010602011771号