道长的算法笔记:Trie字典树
Trie模板
Trie 是一种用于实现字典序快速检索的多叉树结构,Trie 每个节点都有若干的字符指针,若在扫扫描字符串时扫到字符 \(c\),则沿着当前节点 \(c\) 字符指针走向该指针指向的节点。初始化阶段,Trie近包含一个空节点,其所有字符指针均为空。
通过数组模拟字典树,分配树节点的方式与数组模拟静态链表的方式是一样,使用一个索引变量分配节点,与模拟链表中不同的地方在于分配节点使用++idx而非idx++,这种做法相当于利用 idx=0虚设了一个根节点,也即全局声明idx已经完成了初始化。接下来,Trie 主要操作包括插入与查询两个,其核心逻辑都是自顶向下的遍历:

当要插入一个字符串 \(S\),使用指针 \(p\) 指向根节点,依次扫描\(S\)包含的每个字符\(c\)
- 如果 \(p\) 字符指针指向了空指针,则新建一个节点 \(q\),再令 \(p=q\)
- 如果 \(p\) 字符指针指向了已经存在的节点 \(q\),则令 \(p=q\)
- 如果 \(S\) 已经扫描完毕则在当前节点 \(p\) 标记一下
当要查询一个字符串 \(S\),使用指针 \(p\) 指向根节点,依次扫描 \(S\) 包含的每个字符 \(c\)
- 如果 \(p\) 字符指针指向了空指针,说明字符串不存在,结束检索
- 如果 \(p\) 字符指针指向了已经存在的节点 \(q\),则令 \(p=q\),继续检索
- 如果 \(S\) 已经扫描完毕且当前节点 \(p\) 已被标记则认为 \(S\) 存在,反之不存在,结束检索
char str[MAXN];
int son[MAXN][26], cnt[MAXN], idx = 0;
int insert(char str[]){
int p = 0;
for(int i = 0; str[i]; i++){
int u = str[i] - 'a';
if(!son[p][u]){
son[p][u] = ++idx;
}
p = son[p][u]; // 沿着新建的或已存在的节点往下移动
}
cnt[p]++;
}
int query(char str[]){
int p = 0;
for(int i = 0; str[i]; i++){
int u = str[i] - 'a';
if(!son[p][u]){
return 0;
}
p = son[p][u];
}
return cnt[p]; // 末尾标记不为零则说明字符串存在于树中
}
上述代码逻辑详见代码。如果需要删掉某个单词,只需要把插入逻辑都末端增加,改成末端字符减少即可,Trie 除了用于处理字符串的前缀问题与统计问题之外也常被用于解决最大异或对问题及其变体,但在处理数值类型的元素时,Trie 未必是在末尾进行计数,根据题目的需求,有可能会对每一位都进行计数,
最大异或对
给定的 \(N\) 个整数 \(A_1, A_2,...,A_N\) ,要在其中选出两个元素进行 XOR(异或)运算,其中序列长度范围 \(1 ≤ N ≤ 10^5\), 每个元素的数值范围 \(0≤A_i<2^{31}\),要求解出最大对异或对,本题实际是对 Trie 扩展应用,把元素视为二进制数。边插边查,查询的时候,根据贪心思想,如果同层具有相异的元素则朝着相异的方向往下遍历,否则朝着相同的方向往下遍历。
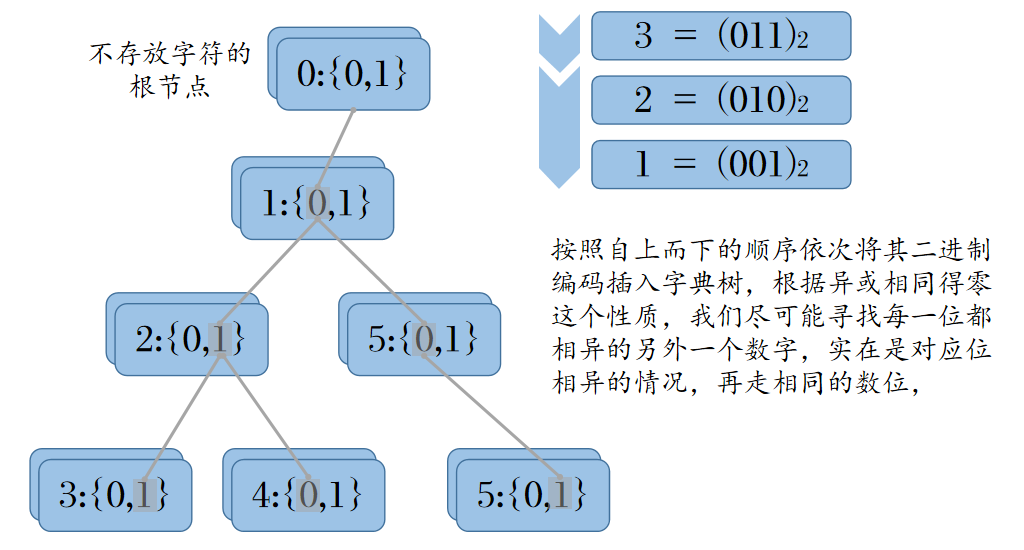
之所以能够能够边插边查,是因为异或满足交换律,\(a \oplus b = b \oplus a\),两两配对构建二元组的复杂度 \(\Theta(n^2)\),但是交换律告诉我们,在计算了 \(a \oplus b\) 之后无需再计算 \(b \oplus a\),因而实际上只需要进行 \(\Theta(\frac{1}{2}n(n+1))\),虽然复杂度的阶数不变,但在代码实现来说,相当于允许我们边插边查,无需先插再查。
#include <bits/stdc++.h>
#include <limits.h>
using namespace std;
#define MAXN 3000005
int sons[MAXN][2], cnt[MAXN], idx;
void insert(int x){
int p = 0;
for(int i = 30; i >= 0; i--){
int u = x >> i & 1;
if(!sons[p][u]){
sons[p][u] = ++idx;
}
p = sons[p][u];
}
cnt[p]++;
}
int query(int x){
int p = 0, ans = 0;
for(int i = 30; i >= 0; i--){
int u = x >> i & 1;
if(sons[p][!u]){
p = sons[p][!u];
ans = 2 * ans + !u;
}else{
p = sons[p][u];
ans = 2 * ans + u;
}
}
return ans;
}
int n, x;
int main(){
scanf("%d", &n);
int ans = 0;
for(int i = 0; i < n ; i++){
scanf("%d", &x);
insert(x);
ans = max(ans, x ^ query(x));
}
printf("%d\n",ans);
return 0;
}
其实本题的 cnt 数组根本不影响答案,因为 32bit int变量转为二进制码长度都是一样的,只要能够走到末尾的叶子节点,即可说明路径对应的数值是存在的。类似的,下面的最长异或路径(AC0146) ,cnt 数组对于答案同样是没有影响的,只有涉及删除操作的时候,cnt 数组才会影响答案,并且彼时 cnt 数组并不在末尾计数,而要对每一个数位都进行计数。
最长异或路径
最长异或路径问题能够转为最大异或对问题,最长异或路径问题中,假设任意两个不相等于的树节点 \(p\)、\(q\),根节点记作 \(r\),我们可以先算从根节点出发,分别到达 \(p\) 与 \(q\) 二者的路径,不妨将其记作,\((p,r)\) 与 \((q,r)\),然后再减掉 \(2\times(LCA(p,q),r)\),其中 \(LCA\) 代表二者的最近公共祖先。

又因为异或的运算系统里面,加减都用 \(\oplus\) 算符,简单化简可知, \((p,r)\oplus (q,r)\) 即为 \(p\) 与 \(q\) 之间连成的异或路径,因而求解最长异或路径的问题转变为找出一对 \((p,r)\)、\((q,r)\) 使得 \((p,r)\oplus (q,r)\) 最大,先对数据预处理,求出所有节点到根节点的距离,至此问题也就变为了最大异或对问题。
#include <bits/stdc++.h>
#include <limits.h>
using namespace std;
#define MAXN 5000005
int head[MAXN], val[MAXN], nxt[MAXN], wgt[MAXN], link;
int sons[MAXN][2], cnt[MAXN], idx;
int arr[MAXN];
void add_edge(int u, int v, int w){
val[link] = v;
wgt[link] = w;
nxt[link] = head[u];
head[u] = link++;
}
void dfs(int u, int parent, int sum){
arr[u] = sum;
for(int i = head[u]; ~i; i = nxt[i]){
int j = val[i];
if(j != parent){
dfs(j, u, sum ^ wgt[i]);
}
}
}
void insert(int x){
int p = 0;
for(int i = 30; i >= 0; i--){
int u = x >> i & 1;
if(!sons[p][u]){
sons[p][u] = ++idx;
}
p = sons[p][u];
}
cnt[p]++;
}
int query(int x){
int p = 0, ans = 0;
for(int i = 30; i >= 0; i--){
int u = x >> i & 1;
if(sons[p][!u]){
p = sons[p][!u];
ans = 2 * ans + !u;
}else{
p = sons[p][u];
ans = 2 * ans + u;
}
}
return ans;
}
int n, x;
int main(){
memset(head, -1, sizeof(head));
scanf("%d", &n);
int a, b, w, ans = 0;
for(int i = 0; i < n - 1; i++){
scanf("%d %d %d", &a, &b, &w);
add_edge(a, b, w);
add_edge(b, a, w);
}
dfs(0, -1, 0);
for(int i = 0; i < n ; i++){
insert(arr[i]);
}
for(int i = 0; i < n ; i++){
ans = max(ans, arr[i] ^ query(arr[i]));
}
printf("%d\n",ans);
return 0;
}
本小节提到的最近公共祖先(LCA)是一个树结构算法题中非常经典的母题,
离线最大异或和
#include <bits/stdc++.h>
#include <limits.h>
using namespace std;
#define MAXN 3500005
int sons[MAXN][2], cnt[MAXN], idx;
int prefix[MAXN];
void insert(int x, int c){
int p = 0;
for(int i = 30; i >= 0; i--){
int u = x >> i & 1;
if(!sons[p][u]){
sons[p][u] = ++idx;
}
p = sons[p][u];
cnt[p] += c;
}
}
/**
* 在一些题解中,(1)与(2)两处的!u与u 会被硬编码写成1与0,
* 这种写法是因为那些作者直接使用 query 计算两个元素异或的结果,然而,
* 注意我们更新 ans 变量的方式,我们是在使用 query 查找能跟当前元素异或最大的另一个元素!
*/
int query(int x){
int p = 0, ans = 0;
for(int i = 30; i >= 0; i--){
int u = x >> i & 1;
if(cnt[sons[p][!u]]){
p = sons[p][!u];
ans = 2 * ans + !u; // (1)
}else{
p = sons[p][u];
ans = 2 * ans + u; // (2)
}
}
return ans;
}
int n, m, x;
int main(){
scanf("%d %d", &n, &m);
int ans = 0;
for(int i = 1; i <= n ; i++){
scanf("%d", &x);
prefix[i] = prefix[i - 1] ^ x;
}
insert(0, 1);
for(int i = 1; i <= n; i++){
if(i > m){
insert(prefix[i - m - 1], -1);
}
// 先更新再插入,因为答案有可能落在[0,i],上文中我们预插了一个 0 用于处理这种情况
ans = max(ans, prefix[i] ^ query(prefix[i]));
insert(prefix[i], 1);
}
printf("%d\n",ans);
return 0;
}
在线最大异或和
待更新…


 浙公网安备 33010602011771号
浙公网安备 33010602011771号