道长的算法笔记：经典逆序对问题

逆序对问题

　　对于一个元素各不相同的数列 $v$，如果 $i<j$ 且 $v[i]>v[j]$，则其构成一个逆序对。

　　出于简化，假设数列元素的大小都落在 $[1,n]$，若不满足此条件可做离散化处理使之满足。如果使用暴力算法，复杂度将会达到 $O(n^2)$，如果数据量达到 $10^5$，这种解法必然超时，我们需要考 $(n\log n)$ 复杂度的算法。

　　一种经典做法做法是以分治思想，使用归并排序对数组排序，并在归并过程计算逆序对。

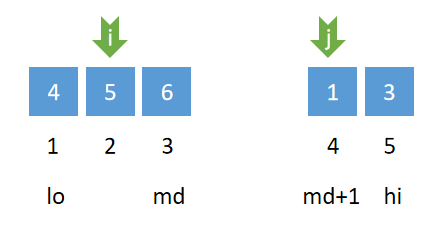
　　如图所示在双指针归并过程中，由于左侧数组 $v[lo:md]$ 与 右侧数组 $v[md+1:hi]$ 都已有序，那么 $v[i]>v[j]$ 意味着，哨兵 $i$ 身后的所有元素都与元素 $v[j]$ 构成逆序对，也就是说，只要触发了 $v[i]>v[j]$ 条件，逆序对个数增加 $md-lo+1$，所以只要做一趟归并即可算出数列里面的所有逆序对个数。

Testing...

　　逆序对问题也会有一些委婉的变体，比如只允许交换相邻元素的情况之下，最少要交换多少次才能使得数列有序。这个问题实际上就是逆序对问题。

Testing...

　　逆序对问题实际亦可使用树状数组与线段树进行查询，因为数列元素的大小都落在 $[1,n]$，我们使用一个数组 $w$ 标记元素 $v[i]$ 是否出现，说白了是用下标做一个映射，如果$v[i]$出现，则把相应元素的坑位赋值 $w[v[i]]=1$，那么逆序对实际上是算 $w$ 数组的 $[v[i]+1:n]$ 区间里面有多少元素被标记，此时逆序对问题也就转为了经典的区间查询问题。