KKT条件

互补松弛性

设原问题和对偶问题的最优值都可以达到且相等，令是原问题的最优解，是对偶问题的最优解，这表明

第一个等式说明最优对偶间隙为零，第二个等式是对偶函数的定义，第三个不等式是根据Lagrange函数关于x求下确界小于等于其在处的值得来，最后一个不等式的成立是因为以及，因此在上面的式子中，两个不等式取等号

可以由此得出一些有意义的结论。例如，由于第三个不等式变为等式，我们知道关于x求极小时在处取得最小值。（Lagrange函数也可以有其他最小点；只是其中一个最小点）

另外一个重要的结论是

 事实上，求和的每一项都非正，因此有

 上述条件称为互补松弛性；它对任意原问题最优解以及对偶问题最优解都成立。我们可以将互补松弛条件写成

 或者等价地

 KKT最优性条件

现在假设函数可微（因此定义域是开集），但是并不假设这些函数是凸函数

1.非凸问题的KKT条件

和前面一样，令和分别是原问题和对偶问题的某对最优解，对偶间隙为零。因为关于x求极小在处取得最小值，因此函数在处的导数为零，即

 因此，我们有

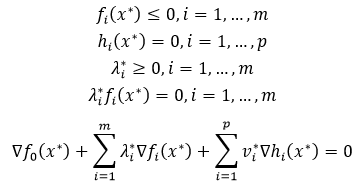
 我们称上式为Karush-Kuhn-Tucker（KKT）条件

2.凸问题的KKT条件

当原问题是凸问题时，满足KKT条件的点也是原、对偶最优解。换言之，如果函数是凸函数，是仿射函数，是任意满足KKT条件的点

 那么对和分别是原问题和对偶问题的最优解，对偶间隙为零

为了说明这一点，注意到前面两个条件说明了是原问题的可行解。因为是x的凸函数；最后一个KKT条件说明在处，Lagrange函数的导数为零。因此，关于x求极小在处取得最小值。我们得出结论

 对目标函数和约束问题可微的任意凸优化问题，任意满足KKT条件的点分别是原、对偶问题最优解，对偶间隙为零

若原问题为凸问题，各个函数可微，对偶间隙为零，则KKT条件为充要条件