二分图相关
写了好多好多,结果学校电脑过热蓝屏了,没保存,我阐释你的梦。
0.1. 增广路
0.1.1. 定义
-
交错路(alternating path)始于非匹配点且由匹配边与非匹配边交错而成。
-
增广路(augmenting path)是始于非匹配点且终于非匹配点的交错路。增广路中边的数量是奇数。形如 (\(\notin M,\in M,\notin M,..., \in M,\notin M\))。
增广路上非匹配边比匹配边数量多 \(1\),如果将增广路上的匹配边和未匹配边反转,则匹配数量会增加 \(1\) 且依然是两种边交错的路。
有交错路不一定有增广路。
0.1.2. 增广路定理 Berge's lemma
匹配 \(M\) 是图的最大匹配,当且仅当 \(M\) 中不含增广路。
考虑转证如下:
- \(M\) 中有增广路时,不是最大匹配。
proof. 设 \(M\) 中存在增广路 \(P\),那么 \(M\oplus P\) 一定是一个比 \(M\) 大的匹配,因为将增广路上的匹配边和未匹配边反转,则匹配数量会增加 \(1\)。(\(\oplus\) 表示对称差)
- \(M\) 不是最大匹配时,存在增广路。
proof. 设 \(M*\) 是比 \(M\) 更大的匹配,考虑图 \(M* \oplus \ M\) ,一定是若干个环或路径的不相交连通块,因为 \(|M*|>|M|\),所以一定存在至少一个路径的连通块中 \(M*\) 比 \(M\) 多一条边,此时这个连通块就是增广路。
这样我们就证明了增广路定理。
0.2. 二分图最大匹配
0.2.1. 增广路算法
有了上面的定理,很容易想到二分图匹配的一个算法流程:
不断寻找增广路,找到则增广一次,将答案加一,否则退出。
简单实现是 \(O(nm)\) 的,因为只会增广 \(O(n)\) 次,则现在需要 \(O(m)\) 寻找到一条增广路。
假设交错路的出发点 \(x\) 均为左部点,现考虑找到交错路的终点集合 \(S\),若存在一个还未匹配的右部点 \(y\in S\),那么路径 \((x,y)\) 是一条增广路(注意到交错路的定义是起点未匹配),这时将这条路径反转,实现增广。
用一个队列维护 bfs(进入过队列的点都属于 \(S\)),扩展出 \(S\),扩展规则为:
-
初始时将未匹配的左部点 \(x\) 加入队列。
-
遍历队列中点的出边,找到右部点 \(y\),如果 \(y\) 存在另一组匹配 \((z,y)\),则将 \(z\) 加入队列。
为了不重复入队扩展,考虑记录 \(y\) 的前驱,与此同时也要记录 \(x\) 的匹配点(其实也是前驱)。
实现起来很简单。
int xlink[N],ylink[N],pre[N];
int find(){
queue<int> q;
for(int i=1;i<=m;i++) pre[i]=0;
for(int i=1;i<=n;i++)
if(!xlink[i]) q.push(i);
while(!q.empty()){
int x=q.front();
q.pop();
for(auto y:g[x]){
if(pre[y]) continue;
pre[y]=x;
if(ylink[y]) q.push(ylink[y]);
}
}
for(int i=1;i<=m;i++) if(!ylink[i]&&pre[i]) return i;
return 0;
}
void getans(){
while(1){
int p=find();
if(!p) return;
ans++;
for(int x=pre[p];x;x=pre[p]){
int t=xlink[x];
ylink[p]=x,xlink[x]=p,p=t;
}
}
}
0.2.2. Hopcroft-Karp 算法
本质上就是 Dinic 算法求解二分图匹配。
将增广路算法里的每次只找一条增广路改进为每轮找最短的不相交的极大增广路集合(maximal set of disjoint shortest Aug path)。
注意是极大而不是最大,因为可能无法找到最大的集合,只能退而求其次找一个无法再增加的集合。
该算法的时间复杂度为 \(O(m\sqrt n)\),而每轮找集合的过程可以做到 \(O(m)\)。在进行完 \(\sqrt n\) 轮 HK 算法后,大部分匹配都已经找全了,接下来通过一些引理来证明剩下的匹配不会超过 \(\sqrt n\),即寻找过程最多不会超过 \(2\sqrt n\) 轮。
记路径 \(P_1,P_2,...,P_k\) 为一组匹配 \(M\) 的最短不相交的极大增广路集合,\(M'\) 为 \(M\) 增广这些路径之后的结果,\(P\) 为 \(M'\) 的一条增广路,\(A=M\oplus(M'\oplus P)=P_1\oplus P_2\oplus \cdots\oplus P_k\oplus P\)。
- Lemma 0.2.2.1. 每一轮寻找到的增广路长度严格大于上一次(\(|P|>l=|P_i|\))。
proof. 分讨 \(P\) 是否与 \(P_i\) 相交。
-
\(P\) 与 \(P_i\) 没有重合的点。此时若 \(|P|=l\),则不符合极大,同样的,若 \(|P|<l\),则不符合最短,故不相交时 \(|P|>l\)。
-
\(P\) 与 \(P_i\) 有重合的点,可以证明此时一定有至少一条边重合,所以有 \(|A|\le |P|+l\times k-2\)。又因为 \(A\) 中有 \(k+1\) 条顶点不相交的增广路,故 \(|A|\ge l\times(k+1)\),否则一定可以找到更短的增广路在前面更新。
所以有 \(l\times(k+1)\le |P|+l\times k-2\),即 \(|P|\ge l+2 > l\),得证。
假定最坏情况下该算法在第 \(\sqrt n\) 轮后没有结束,令 \(M\) 为此时的中间结果,\(M*\) 为最大匹配。
- Lemma 0.2.2.2. \(|M*| - |M|\le \sqrt n\)。
proof. 由 Lemma 0.2.2.1. 可知,第 \(i\) 轮寻找的增广路长度一定不小于 \(i\),故 \(M\) 中存在的增广路长度一定不小于 \(\sqrt n+1\) 。
根据流分解定理,因为 \(M*\) 是最大匹配,所以可以得知路径的连通块一定全部满足 \(M*\) 比 \(M\) 多一条边,即有 \(x\) 个这样的连通块,就存在 \(x\) 条不相交的增广路。
而 \(M\) 中一定有 \(|M*| - |M|\) 条不相交的增广路,即对于新图 \(M* \oplus \ M\),有 \(|M*| - |M|\) 条路径的连通块中 \(M*\) 比 \(M\) 多一条边。
每条不相交的增广路长度的最小值为 \(\sqrt n+1\),至少占用了 \(\sqrt n\) 个点,而总点数不会超过 \(n\),所以路径连通块个数应不超过 \(\frac{n}{\sqrt n}= \sqrt n\),则有 \(|M*| - |M|\le \sqrt n\)。
实现起来先 bfs 再 dfs,本质上就是 Dinic 算法。
于是同理我们称 Dinic 算法在求解二分图最大匹配时,复杂度为 \(O(m\sqrt n)\)。
int xlink[N],ylink[N],vis[N],dx[N],dy[N];
int mx;
bool bfs(){
mx=inf;
queue<int> q;
for(int i=1;i<=n;i++) dx[i]=inf;
for(int i=1;i<=m;i++) dy[i]=inf;
for(int i=1;i<=n;i++){
if(!xlink[i]){
dx[i]=0;
q.push(i);
}
}
while(!q.empty()){
int x=q.front();
q.pop();
if(dx[x]>mx) break;
for(auto y:g[x]){
if(dy[y]!=inf) continue;
dy[y]=dx[x]+1;
if(!ylink[y]) mx=dy[y];
else dx[ylink[y]]=dy[y]+1,q.push(ylink[y]);
}
}
return mx!=inf;
}
bool find(int x){
for(auto y:g[x]){
if(vis[y]||dy[y]!=dx[x]+1) continue;
vis[y]=1;
if(ylink[y]&&dy[y]==mx) continue;
if(!ylink[y]||find(ylink[y])){
xlink[x]=y,ylink[y]=x;
return 1;
}
}
return 0;
}
int work(){
int ans=0;
for(int i=1;i<=n;i++) xlink[i]=0;
for(int i=1;i<=m;i++) ylink[i]=0;
while(bfs()){
for(int i=1;i<=n;i++) vis[i]=0;
for(int i=1;i<=n;i++)
if(!xlink[i]) ans+=find(i);
}
return ans;
}
0.3. Hall 定理
0.3.1. 内容
设二分图 \(G=\langle X, Y, E \rangle, |X| \leq |Y|\),则 \(G\) 中存在 \(X\) 到 \(Y\) 的完美匹配(大小为 \(|X|\) 的匹配)当且仅当对于任意的 \(A \subset X\),均有 \(|A|\leq|N(A)|\),其中 \(N(A)=\bigcup_{v_i \in A}{N(v_i)}\),是 \(A\) 的邻域,即 \(N(A)=\{ b \ | \ \exists a \in A,(a,b)\in E \}\)。
0.3.2. 证明
该定理的必要性很显然,因为若存在 \(A\),使得 \(|N(A)|<|A|\),那一定不会有一个完美匹配。
对于充分性,则可以从逆否命题的角度进行证明。
(说句闲话,否命题和命题的否定不是一个东西,高中数学考的一般是命题的否定;否命题和逆命题是等价命题,原命题和逆否命题是等价命题)
原命题:若 \(\forall A \subset X\),均有 \(|A|\leq|N(A)|\),则 \(G\) 中存在完美匹配。
命题的否定:若 \(\forall A \subset X\),有 \(|A| \leq |N(A)|\),则 \(G\) 中不存在完美匹配。
否命题:若 \(\exists A \subset X\),有 \(|A| > |N(A)|\),则 \(G\) 中不存在完美匹配。
逆否命题:若 \(G\) 中不存在完美匹配,则 \(\exists A \subset X\),有 \(|A| > |N(A)|\)。
扯远了,现在需要转证其逆否命题。
(upd:勘误,详见 link,逆否命题是对的)。
考虑设现在图的最大匹配 \(M\) 满足匹配点数量不足 \(|x|\),找到 0.2.1. 中的交错路的终点集合 \(S\),取 \(T=\overline S\),此时二分图被分成四个部分 \(S_x,S_y,T_x,T_y\)。
- Lemma 0.3.2.1. \(S_x\) 和 \(T_y\) 中没有连边。
proof. 反证,假设存在一条边,分情况讨论该条边 \(e(x,y)\) 的类型:
-
\(e \notin M\),不合法,因为会从 \(x\in S_x\) 扩展到 \(y\in T_x\),故 \(y\) 一定在 \(S_y\) 中。
-
\(e \in M\),同样不合法,因为此时 \(x\) 的前驱是 \(y\),故 \(y\) 一定在 \(S_y\) 中。
- Lemma 0.3.2.2. \(|S_x|>|S_y|\)。
proof. 因为现在图的最大匹配 \(M\) 满足匹配点数量不足 \(|x|\),故 \(S_x\) 与 \(S_y\) 两两匹配之外,一定有至少一个左部点 \(x\in S_x\) 是未匹配的,其作为初始点(也可以理解为导火线)将右部点加入队列。
现在我们取 \(A=S_x\),则 \(N(A)=S_y\),有 \(|S_x|>|S_y|\),即 \(|A|>|N(A)|\),逆否命题得证,原命题得证。
Q.E.D.
0.3.3. 引理
若二分图 \(G=(X,Y,E)\) 的度数为 \(k\),则存在完美匹配。
- 证明
隐含的信息是 \(|X|=|Y|\),因为 \(|X|\times k=|Y|\times k\)。
若左边选了集合 \(A\) 里的点,那么一定有 \(|A|\times k\) 条边连向右边,而连向每一个右部点的边数又不能超过 \(k\),所以有 \(|A|\times k\leq |N(A)|\times k\),即 \(|A|\leq |N(A)|\),由 Hall 定理可知,一定存在完美匹配。
- 应用
\(n\times n\) 的拉丁方,已经填了 \(k\) 行合法,则一定可以填完。
proof. 只考虑能不能填上第 \(k+1\) 行,剩下用归纳法证明。对于第 \(k+1\) 行,将每列的下标作为左部点,能填的元素权值作为右部点,连边 \((x,y)\) 表示第 \(x\) 列能填 \(y\),由于已经填了 \(k\) 行了,所以每一列只有 \(n-k\) 个元素可以填,而对于每个元素,在这一行也只有 \(n-k\) 个位置可以填,也就是说度数为 \(n-k\) 的二分图,存在完美匹配,即可以填完。
0.4. Kőnig 定理
0.4.1. 相关概念
不写了,见 oi-wiki。
对于二分图 \(G=(V,E)\),若 \(A \subseteq V\) 为独立集,则 \(\overline A\) 为点覆盖。
proof. \(A\) 为独立集 \(\Leftrightarrow \forall(a,b)\in E,a\notin A \vee b \notin A \Leftrightarrow \forall(a,b)\in E,a\in \overline A \vee b \in \overline A \Leftrightarrow \overline A\) 为点覆盖。
故最大独立集 \(=\) 点数 \(-\) 最小点覆盖。
0.4.2. 内容及证明
二分图 \(G\) 的最大匹配数(\(MM\))等于最小点覆盖数(\(MVC\))。
从 \(|MVC|\ge |MM| \wedge |MVC| \le |MM|\) 来证明。
- \(|MVC|\ge |MM|\)
这个比较显然,因为最大匹配的边一定是独立的,必须选出至少 \(|MM|\) 个端点来覆盖它们。
- \(|MVC|\le |MM|\)
proof. 只需要证明存在一组大小为 \(|MM|\) 的点覆盖,那么最小点覆盖大小一定不大于这组覆盖。
仍然考虑 0.3.2. 提到的 \(S\) 和 \(T\),它们现在是当前图最大匹配 \(M\) 的交错路终点集合以及它的补集。
由于 \(S_x\) 与 \(T_y\) 中没有边,现在只考虑 \((S_x,S_y)\)、\((T_x,S_y)\)、\((T_x,T_y)\) 三种边。
容易知道 \((T_x,S_y)\) 一定是非匹配边,否则 \(x\) 会被加入 \(S_x\),所以匹配边一定是 \((S_x,S_y)\) 或 \((T_x,T_y)\)。
现在考虑证明 \(S_y\) 和 \(T_x\) 中均不存在非匹配点。
前者,因为这是最大匹配,所以不能存在增广路,也就是 \(S_y\) 中不能存在未匹配点;后者,因为初始的扩展会把未匹配的 \(x\) 加入 \(S_x\),所以 \(T_x\) 不能存在未匹配点。得证。
也就是说我们可以选择 \(S_y\) 和 \(T_x\) 两个集合作为点覆盖,可以覆盖到所有的边(它们所连出去的边以及它们之间的连边),而 \(|S_y+T_x|=|MM|\),所以这组点覆盖大小等于最大匹配。命题得证。
\(|MVC|\ge |MM| \wedge |MVC| \le |MM| \Rightarrow |MVC| = |MM|\) 。
这样我们就证明了 Kőnig 定理。
0.4.3. 其他相关
- DAG 最小路径覆盖 (1)
定义为用最少数量的路径覆盖所有的点,满足路径没有顶点重合(vertex disjoint),路径长度可以为 \(0\)。
DAG 最小路径覆盖 \(=\) 点数 \(-\) 二分图最大匹配。
这个二分图构造为,对于原 DAG \(G=(V,E)\) 中的每一条边 \((a,b)\in E\),连接二分图中的左部点 \(a\) 与右部点 \(b\)。
匹配一次就相当于把两条路径合并,可以理解为一条路径会被终点统计到,因为终点没有匹配。
- DAG 最小路径覆盖 (2)
路径和链的覆盖问题都是看语境的。
这里定义为用最少数量的路径覆盖所有的点,点可以重合。
考虑建立二分图 \(G*\) 中存在边 \((a,b)\) 当且仅当原 DAG \(G\) 中 \(a\) 可达 \(b\)。
接下来就和 (1) 问题一样了,因为如果用到了一条可达的路径,就相当于强制钦定了不经过中间的点。
可达性可以用 bitset 优化传递闭包。
- DAG 最小路径覆盖 (3)
是 0.6.1. 的应用。
定义为用最少数量的路径覆盖所有的边,边都可以重合。
定义偏序关系 \(i\preceq j\) 当且仅当存在一条路径先经过边 \(e_i\) ,再经过 \(e_j\),也即 \(e_i\) 的起点可以到达 \(e_j\) 的终点。
容易发现该偏序关系具有三个性质,所以我们将问题转换成偏序集的最小链覆盖问题,故又变成了 (2) 问题。
若不是 DAG,则可以采用上下界网络流进行求解,在此不做赘述。
0.5. UVG 游戏
Undirected Vertex Geography Game
无向图地理游戏,指在一个无向图中,只有一个起点,上面有一个棋子,两个玩家轮流沿着边推动棋子,不能走重复的点,无法行动则失败。
0.5.1. 结论
如果无向图 \(G\) 的所有最大匹配都经过起点,则先手必胜;否则如果存在一组最大匹配使得该匹配不经过起点,则先手必败。
0.5.2. 证明
仍然从两个方面来证明充要,采用反证法。
- 无向图 \(G\) 的所有最大匹配都经过起点,则先手必胜。
proof. 先手任意选择一个 \(MM\),策略为 move-along \(MM\),即顺着最大匹配走,此时后手一定只能走一条非匹配边。
假设先手失败,有两种情况,分别为“走到一个该匹配下的匹配点,但是匹配边另一端的点已经被访问过”和“走到一个非匹配点”,前者显然不可能,而后者可以得到走过的这条路径为交错路,将其反转后仍然是最大匹配,且不再经过起点,所以假设不成立,先手必胜。
- \(G\) 存在一组最大匹配使得该匹配不经过起点,则先手必败。
proof. 先手任意选择一个点 \(x\) 走过去,可以证明存在 \(MM\) 经过 \(x\),原因是若不存在一定可以选上起点到 \(x\) 的边使得匹配严格变大。于是此时后手策略为 move-along \(MM\),假设先手获胜,则一定走到了一个在该匹配下的非匹配点(匹配点但是另一端的点已经被访问过的情况显然不合法),而起点也是非匹配点,容易发现这是一条增广路,可以将匹配扩大,所以不符合最大匹配,假设不成立,先手必败。
关于为什么不存在走到匹配点但是另一端的点已经被访问过的情况,容易发现当走过一条匹配边时,整张图上匹配边的两端访问状态相同,则走一条非匹配边后,一定有该点所在匹配边另一端是未被访问的点。
0.6. Dilworth 定理
0.6.1. 相关概念
- 偏序集
若集合 \(S\) 上的一个二元关系 \(\preceq\) 具有 自反性、反对称性、传递性,则称 \(S\) 是偏序集(partially ordered set,poset),\(\preceq\) 为其上一偏序(partial order)。
- 链与反链
对偏序集 \(S\) 和其上的偏序 \(\preceq\),称 \(S\) 的全序子集为链(chain)。若 \(S\) 的子集 \(T\) 中任意两个不同元素均不可比(即 \((\forall\ a,b \in T)\ a \neq b \implies (a \npreceq b \land b \npreceq a)\)),则称 \(T\) 为反链(antichain)。
对偏序集 S 和其上的偏序 \(\preceq\),我们将偏序集 \(S\) 的最长反链长度称为宽度(partial order width)。
0.6.2. 内容及证明
对有限偏序集 \(S\) 和其上的偏序 \(\preceq\),满足最小链覆盖等于最长反链长度。
注意 Dilworth 定理定义在偏序集中,或者说是一个已经传递闭包后的 DAG,那么这里链覆盖能不能经过重复点是一样的。
如果在普通 DAG 中,并不去求它的传递闭包,不可比定义为不可达,那么这里链覆盖实际上就是点可以相交的路径覆盖。
上者引自 dwt 的博客。
设 \(A\) 为任意一条反链,\(P\) 是最小链覆盖。
从两方面说明。
- \(|P|\ge |A|\)
proof. 显然,因为若存在反链 \(A\),一定不存在一条路径可以覆盖 \(A\) 中的两个点。
故反链大小不能超过最小的链覆盖数量。
- 当 \(A\) 是最大反链时,存在 \(|A|=|P|\)
proof. 对于一张偏序集构成的 DAG,对它构造二分图 \(G\)(因为偏序集已经做好传递闭包了,所以我们直接连边即可)。
于是有 \(|P|=n-|MM|\),根据 Kőnig 定理,有 \(|MM|=|MVC|\),所以现在只需要证明存在 \(|A|=n-|MVC|\)。
现给出构造:若点 \(i\) 满足 \(x_i\notin MVC \wedge y_i \notin MVC\),则将 \(i\) 加入到 \(A\) 中。
考虑从两方面证明该构造的正确性:
- \(A\) 为一个反链。
proof. 采用反证法,若 \(A\) 不是反链,当且仅当存在 \(i\) 可达 \(j\),有连边 \(x_i\rightarrow y_j\),因为 \(x_i\notin MVC \wedge y_i \notin MVC\wedge x_j\notin MVC \wedge y_j \notin MVC\),所以没有点可以覆盖边 \(x_i\rightarrow y_j\),故这不是点覆盖,假设不成立。
- \(|A|=n-|MVC|\) 。
我们容易发现只有 \(MVC\) 在同一行不存在两个同时选择的点时,才有 \(|A|=n-|MVC|\),其余情况下均有 \(|A|\ge n-|MVC|=|P|\)。
而前面已经证明过 \(|A|\le|P|\),所以有 \(|A|=|P|\)。
于是我们证明了 Dilworth 定理,同时得到了一个最大反链的构造方法——求出最小点覆盖,选择两部点都不在最小点覆盖中的点。
所以还可以得到偏序集二分图的性质,即为不存在 \(i\) ,使得 \(x_i\) 与 \(y_i\) 均在最小点覆盖中。
这一点其实也可以予以证明:
假设 \(y_i\in S_y\wedge x_i\in T_x\),则一定有 \(x_j\) 是 \(y_i\) 的匹配点且 \(x_j\in S_x\),若 \(x_i\) 的匹配点为 \(y_k\in T_y\),根据偏序关系可知一定存在 \(j\) 可达 \(k\),故 \(x_j\) 与 \(y_k\) 有连边,则 \(y_k\) 应在 \(S_y\) 中,假设不成立。
0.7. 二分图最佳匹配
0.7.1. 概念
- 二分图最大权完美匹配
二分图中边权和最大的完美匹配。
我们认为,在这张二分图中,任意一个左部点都有和所有右部点的连边,左右点数相等,且边权均为非负整数,称其为标准情况,对于任意一张二分图,可以通过调整来达到该限制。
具体地,若边数不够,则添加边权为 \(-\infty\) 的边;若边权为负,则把所有边都加上一个偏移量,因为我们选出的边的数量是固定的,所以可以保证正确性。
若左右点数不相等,则将小的一边补齐,划归到非负情况下添加 \(0\) 边。
于是使用 KM 算法(匈牙利算法)就可以解决该问题。
- 二分图带权最大匹配
二分图中边权和最大的最大匹配。可以通过加入边权为 \(-\infty\) 的边来化归到上一个问题。
- 二分图最大权匹配
二分图中边权和最大的匹配。可以通过加入边权为 \(0\) 的边来化归到第一个问题,注意到如果此时二分图中有负边,则将其变成 \(0\)。
0.7.2. KM 算法(匈牙利算法)
其实匈牙利算法是解决最佳匹配而不是最大匹配的说...
以 \(O(n^3)\) 的时间复杂度解决二分图最大权完美匹配的算法。
引入一些概念:
-
可行顶标:给每个节点 \(i\) 分配一个权值 \(l(i)\),称该权值为 \(i\) 的顶标,对于所有边 \((u,v)\) 满足 \(w(u,v) \leq l(u) + l(v)\),则称 \(l(i)\) 是一组可行顶标。
-
相等子图:在一组可行顶标下原图的生成子图,包含所有点但只包含满足 \(w(u,v) = l(u) + l(v)\) 的边 \((u,v)\)。
- Lemma 0.7.2.1. 对于某组可行顶标,如果其相等子图存在完美匹配 \(M\),那么,\(M\) 就是原二分图的最大权完美匹配。
proof. 对于该完美匹配 \(M\),有 \(val(M)=\sum l(x_i)+l(y_i)\)。
设原二分图的最大权完美匹配为 \(M'\),则一定有 \(val(M')=\sum w(u,v)\le \sum l(x_i)+l(y_i)=val(M)\)。
所以 \(M\) 一定是原二分图的最大权完美匹配。
于是我们有了一个简单的想法:初始随即设定一组可行顶标,通过不断的调整使得相等子图为完美匹配。
考虑对于初始的相等子图跑最大匹配,可以得到下图的情况:
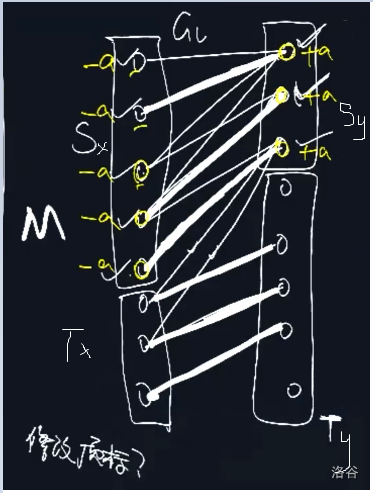
沿用 0.3.2. 中提到的 \(S\) 和 \(T\),此时图被分成四个部分,在 0.3.2.1. 中我们证明了 \(S_x\) 和 \(T_y\) 中不存在连边,在 0.4.2. 中则证明了\((T_x,S_y)\) 一定是非匹配边。
考虑调整可行顶标,我们给 \(S_x\) 中的点顶标 \(-a\),给 \(S_y\) 中的点顶标 \(+a\),使得:
-
\(S_x\) 与 \(S_y\) 中连边不变。
-
\(T_x\) 与 \(T_y\) 中连边不变。
-
\(T_x\) 与 \(S_y\) 中连边可能减少。这个其实没什么影响,因为去掉的边一定都是非匹配边,且两端点均为匹配点。
-
\(S_x\) 与 \(T_y\) 中可能产生连边。
考虑 \(a\) 值的选择,应该是 \(\min \{ l(x_i) + l(y_j) - w(i,j)\ |\ x_i\in{S_x} , y_j\in{T_y} \}\),即松弛量最小值。
当一条新的边 \((x,y)\) 加入相等子图后有两种情况:
-
\(y\) 是未匹配点,则找到增广路,重新求 \(S\) 和 \(T\)。
-
\(y\) 和 \(T_x\) 中的点已经匹配,则顺着一直走下去,修改 \(S\) 和 \(T\) 的部分值。
由于每次修改至少使 \(S_y\) 集合增加一个,所以至多修改 \(n\) 次顶标,就可以找到增广路了。
于是我们得到了一个算法流程:
-
随便选择一组可行顶标,求出 \(M\)、\(S\) 和 \(T\)。
-
当 \(|M|<n\) 时执行如下操作直到 \(|M|=n\)(while):
- 求出 \(a=\min \{ l(x_i) + l(y_j) - w(i,j)\ |\ x_i\in{S_x} , y_j\in{T_y} \}\)。
- 修改可行顶标权值,通过一条边的增加来计算 \(|M|\) 是否会扩大。
- 对应修改 \(S\) 和 \(T\)。
试分析复杂度。
首先找到一次增广路需要 \(O(n)\) 次的修改 \(l(i)\),而总共需要 \(n\) 条增广路,所以 while 操作会执行 \(O(n^2)\) 次。
考虑内部的三个操作,操作 \(2\) 在两次重新求 \(S\) 和 \(T\) 之间,会把图上的每条边遍历不超过一次,所以是 \(O(n^2)\) 的,操作 \(3\) 若需要重新求 \(S\) 和 \(T\),也是 \(O(n^2)\) 的,但由于只会有 \(n\) 次需要重新求,所以均摊下来两个操作都是 \(O(n^3)\);故复杂度瓶颈成了 \(O(n^2)\) 的操作 \(1\),它让总复杂度变成了 \(O(n^4)\)。
考虑优化该操作使得复杂度变成 \(O(n^3)\)。
记 \(slack(y)=\min \{ l(x) + l(y) - w(x,y)\ |\ x\in{S_x} \}\)。
考虑三种操作的复杂度:
-
在求 \(a\) 时,遍历每一个 \(T_y\) 中的 \(y\),求 \(slack\) 的最小值。
-
修改可行顶标时,\(slack(y)\gets slack(y)-a\)。
-
扩展增加 \(S_x\) 时,修改 \(slack(y)\),可能变得更小,该操作均摊只会进行 \(O(n^2)\) 次。
单次操作复杂度为 \(O(n)\),所以总时间复杂度为 \(O(n^3)\)。
实际实现的时候并不需要先求出最大匹配再找到 \(a\),可以直接从每个点出发增广。
bool check(int y){
sy[y]=1;
if(ylink[y]){
q.push(ylink[y]);
sx[ylink[y]]=1;
return 0;
}
while(y){
ylink[y]=pre[y];
swap(y,xlink[pre[y]]);
}
return 1;
}
void bfs(int st){
q.push(st);
sx[st]=1;
while(1){
while(!q.empty()){
int x=q.front();
q.pop();
for(int y=1;y<=n;y++){
if(sy[y]) continue;
ll t=lx[x]+ly[y]-w[x][y];
if(slack[y]>=t){
pre[y]=x;
if(t) slack[y]=t;
else if(check(y)) return;
}
}
}
ll a=inf;
for(int y=1;y<=n;y++)
if(!sy[y]) a=min(a,slack[y]);
for(int i=1;i<=n;i++){
if(sx[i]) lx[i]-=a;
if(sy[i]) ly[i]+=a;
else slack[i]-=a;
}
for(int y=1;y<=n;y++) if(!sy[y]&&!slack[y]&&check(y)) return;
}
}
其实看代码分析复杂度更清晰了,由于是从每一个点出发寻找增广路,所以 while(1) 操作至多进行 \(n\) 次。
KM 算法在找到最大权完美匹配的同时,也找到了一组权值和最小的可行顶标,所以若要求解最小可行顶标,可以使用 KM 算法。
注意如果左右点数不相等只能求解最小非负可行顶标。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号