二分查找法

1.概念

        假如现在有1~100个数，你的目标是以最少的次数猜到这个数字。你每次猜测后，我会说小了、大了或猜对了。假设你从1开始依次往上猜，猜测过程可能会是这样。

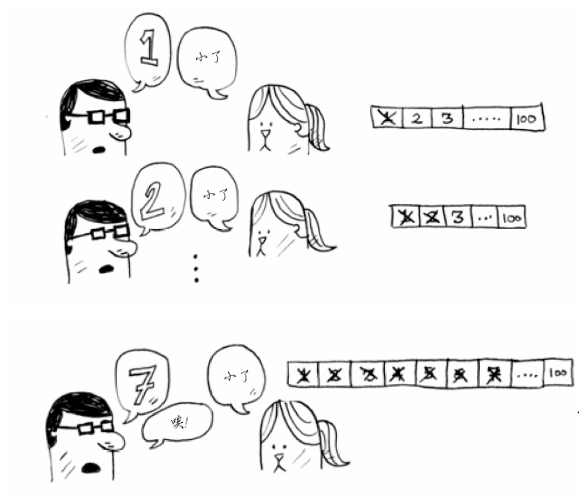
        这是最简单的查找方法，更准确的说法是傻找。每次猜测都只能排除一个数字。如果我想的数字是99， 你得猜99次才能猜到！

        下面是一种更佳的猜法。从50开始。

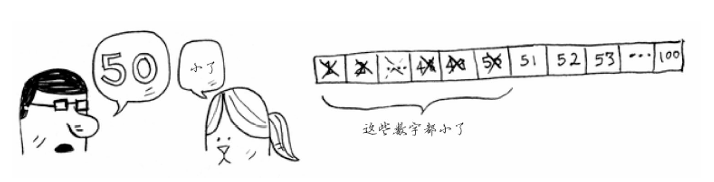
        虽然猜小了，但排除了一半的数字！至此，你知道1～50都小了。接下来，你猜75。

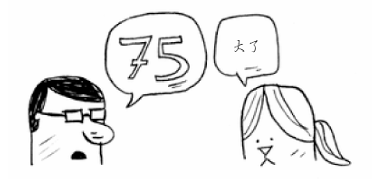
        这次猜大了，那余下的数字又排除了一半！使用二分查找时，你猜测的是中间的数字，从而每次都将余下的数字排除一半。接下来，你猜63（50和75中间的数字）。

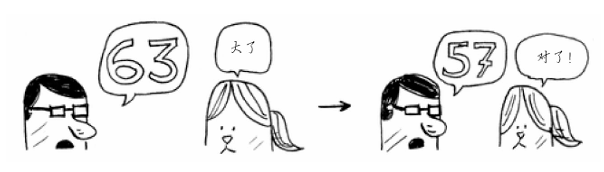
        这就是二分查找，每次猜测排除的数字个数如下。

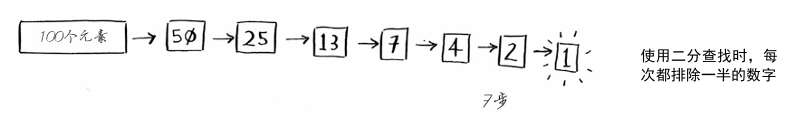
        一般而言，对于包含n个元素的列表，用二分查 找最多需要log2n步，而简单查找最多需要n步。

2.代码示例

2.1 C代码

#include <stdio.h>

/**
 * 二分查找函数（适用于升序数组）
 * @param arr 已排序的整型数组
 * @param len 数组长度
 * @param target 目标查找值
 * @return 目标值在数组中的索引（从0开始），未找到返回-1
 */
int binary_search(int arr[], int len, int target) {
    int left = 0;              // 左边界索引
    int right = len - 1;       // 右边界索引
    int mid = 0;

    while (left <= right) {    // 左闭右闭区间 [left, right]
         mid = left + (right - left) / 2; // 防溢出写法

        if (arr[mid] == target) {
            return mid;        // 找到目标值，返回索引
        }
        else if (arr[mid] < target) {
            left = mid + 1;    // 目标在右侧，收缩左边界
        }
        else {
            right = mid - 1;   // 目标在左侧，收缩右边界
        }
    }

    return -1; // 未找到目标值
}

int main() {
    // 示例测试
    int test_array[] = { 2, 5, 8, 12, 16, 23, 38, 45, 56, 72 };
    int length = sizeof(test_array) / sizeof(test_array[0]);

    // 测试用例
    printf("查找 23：索引=%d\n", binary_search(test_array, length, 23)); // 应返回5
    printf("查找 45：索引=%d\n", binary_search(test_array, length, 45)); // 应返回7
    printf("查找 3：索引=%d\n", binary_search(test_array, length, 3));  // 应返回-1

    return 0;
}

var code = "d02689ab-53ef-483a-bb8f-713588e7a47b"

2.2 示例代码注意项

         在二分查找或类似算法中，计算中间索引 mid 时，使用 int mid = left + (right - left) / 2; 而不是直接 int mid = (left + right) / 2;，主要是为了防止整数溢出。

        备注：直接写法的风险：(left + right) / 2，当 left 和 right 都是较大的正整数时（接近 INT_MAX），left + right 可能会超过 int 类型的最大值（例如 INT_MAX = 2,147,483,647），导致整数溢出。

int left = 2000000000;
int right = 2100000000;
int mid = (left + right) / 2; // left + right = 4,100,000,000 > INT_MAX，溢出为负数！

3.在嵌软开发中的应用

        在嵌入式系统中，二分法（二分查找、二分逼近）因其高效的 O(log n) 时间复杂度和低内存开销，被广泛应用于资源受限的场景。

• 应用场景：嵌入式设备中常存储静态配置表（如传感器校准表、PT1000温度-电阻对照表、酒精密度与温度对照表等）。

• 代码示例：

// 温度-ADC值对照表（按温度升序排列）
const struct { float temp; uint16_t adc; } calib_table[] = {
    {-10, 100}, {0, 250}, {25, 500}, {50, 750}, {100, 1000}
};

// 二分法查找ADC值对应的温度
float adc_to_temp(uint16_t adc_val) {
    int left = 0, right = sizeof(calib_table)/sizeof(calib_table[0]) - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (calib_table[mid].adc == adc_val) {
            return calib_table[mid].temp;
        } else if (calib_table[mid].adc < adc_val) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1.0f; // 未找到
}

• 优势：比线性查找更快，适合实时性要求高的场景。

3.1总结

        二分法在嵌入式领域的核心优势是 高效+低资源消耗，尤其适合实时性要求高的场景、资源受限的系统（如MCU仅有几KB内存）、需要快速检索静态数据的应用。通过合理设计，可以显著提升嵌入式系统的性能和响应速度。