激活函数深入理解

一. Relu嵌套效果

f = lambda x: (F.relu(2 * (F.relu(3 * x - 1)) + 3))
x = torch.arange(-50, 50, 0.5)
mb.plt.plot(x, f(x))

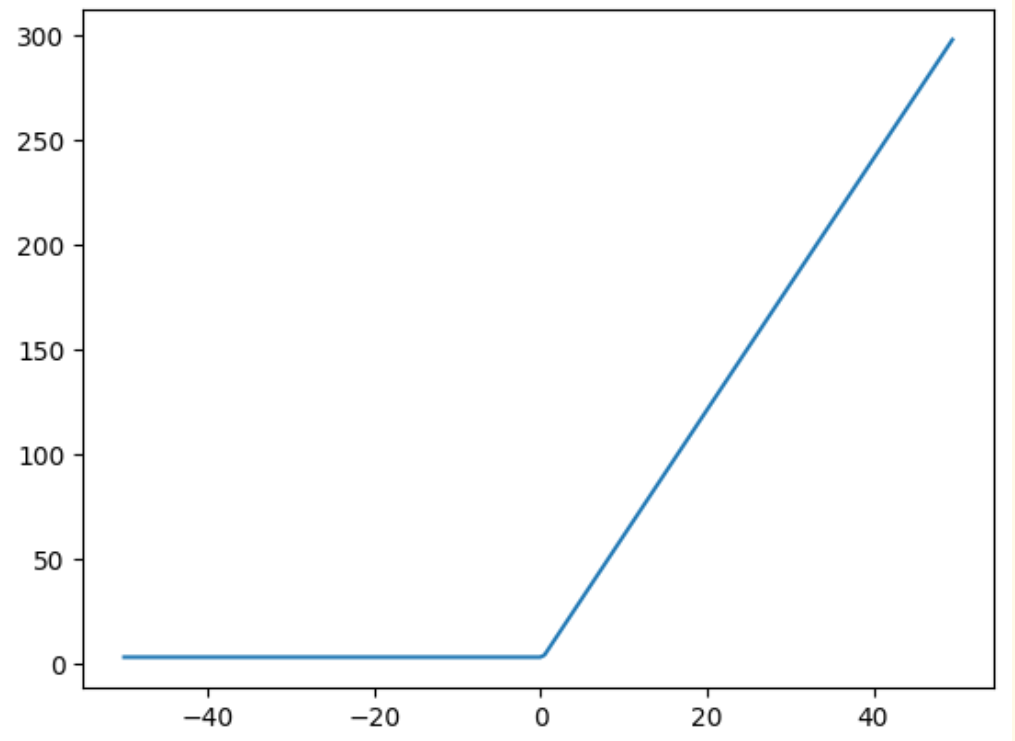
可以看出多个Relu的嵌套之后结果仍然为一个Relu函数。

二. Relu加和效果

f = lambda x:F.relu(1 * x - 1) + F.relu(-1 * x + 10) + F.relu(2 * x - 10) + F.relu(0.5 * x)
x = torch.arange(-50, 50, 0.5)
mb.plt.plot(x, f(x))

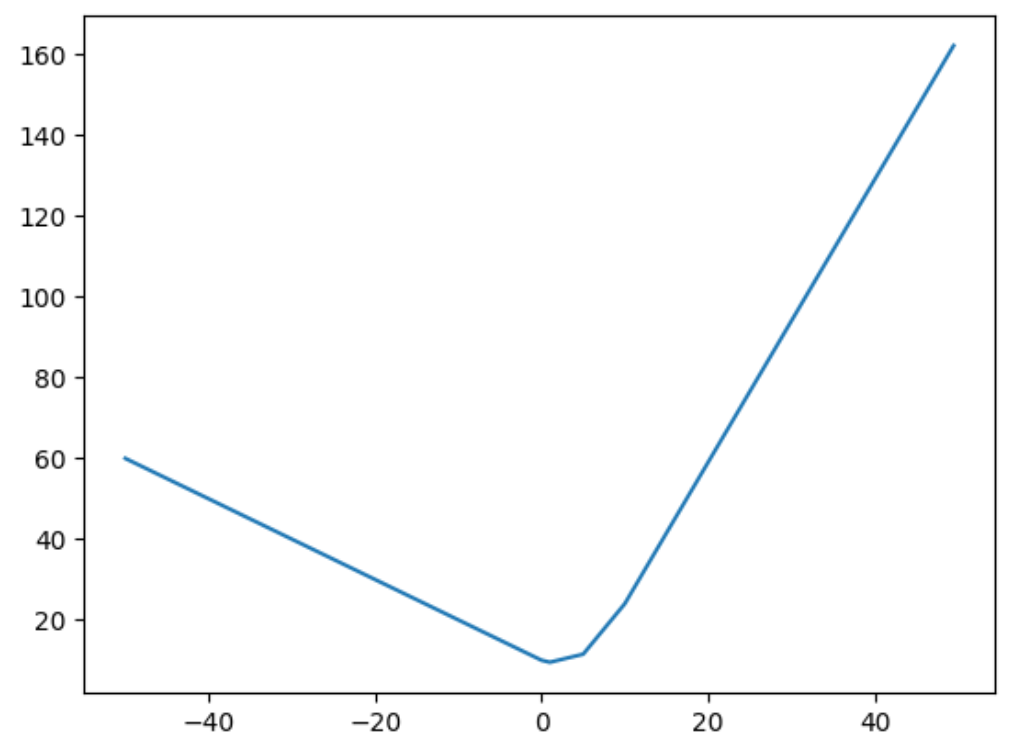
可以看出多个Relu的加和操作可以拟合出任意的曲线。

三. Relu加和结合嵌套的效果

f = lambda x: (F.relu(2 * (F.relu(3 * x - 1) + F.relu(1 * x + 10) + F.relu(1 * x - 10)) + 3) + 
               F.relu(4 * (F.relu(1 * x - 1) + F.relu(3 * x + 10) + F.relu(2 * x - 10)) + 3))
x = torch.arange(-50, 50, 0.5)
mb.plt.plot(x, f(x))

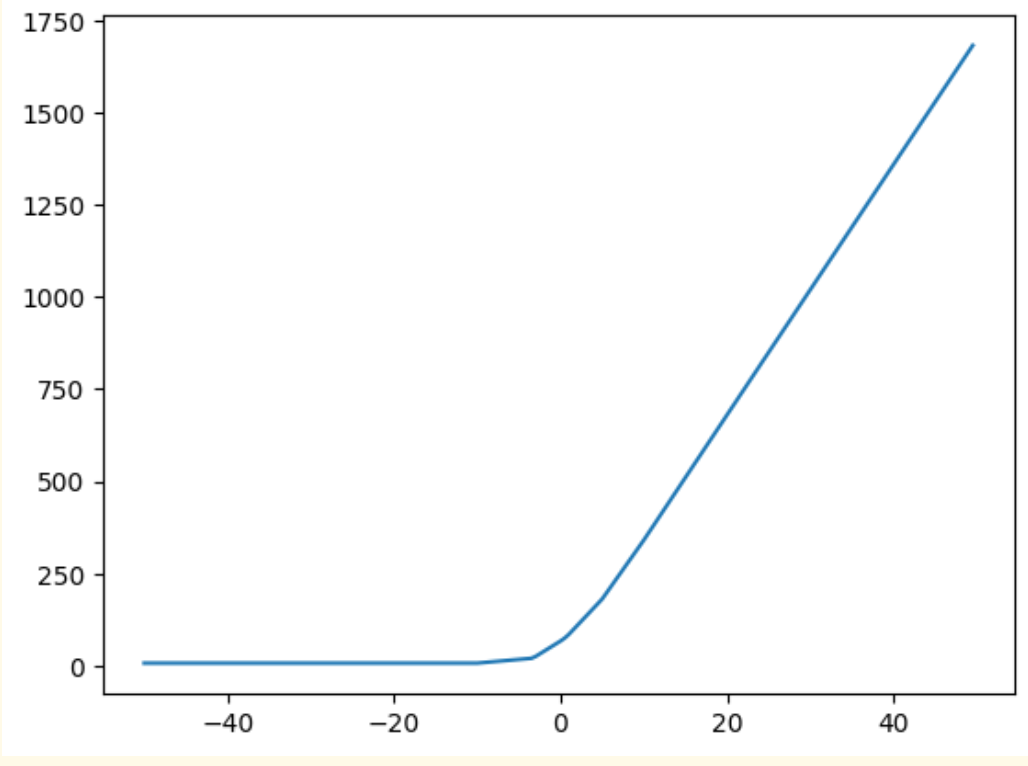
可以看出如果足够复杂依然可以拟合出任意曲线。

四. 思考

由上图可以发现多个Relu的叠加可以产生很复杂的函数曲线，所以神经网络中以全连接为例，先做\(w^T*x\)再做激活再把各个激活后的值相加是可以产生一个复杂函数的，如果网络结构一旦定下来，此时这个网络的函数大体的函数形式就已经定下来了，接下来的训练只是根据每一个样本数据做一些参数上的调整，比如上图中的线的陡峭程度等。以分类的网络为例，最后假设分n个类，那么网络最后的节点数一般都为n个，其中每个节点都代表了一个复杂的函数

根据上面的图可以看出足够多的relu函数相加可以拟合任意曲线，那么为什么网络不做的足够宽呢？

1. 网络更深，每一层要做的事情也更加简单：第一层学习到了边缘，第二层学习到了简单的形状，第三层开始学习到了目标的形状，更深的网络层能学习到更加复杂的表达。如果只有一层，这很难做到。每一层都是一个复杂的曲线（多个Relu的叠加结果）简单来说就是下一层可以利用上一层学到的东西进而学出更深刻的东西，所以要做深。
2. 网络变宽可知Relu叠加的个数变多了，此时曲线的拟合能力提升了，会拟合的更好，但是也会带来一定的问题，就是参数量带来了大量的增加（想想全连接)