最近公共祖先（LCA）

原作者：董晓算法 https://www.cnblogs.com/dx123/p/16320465.html

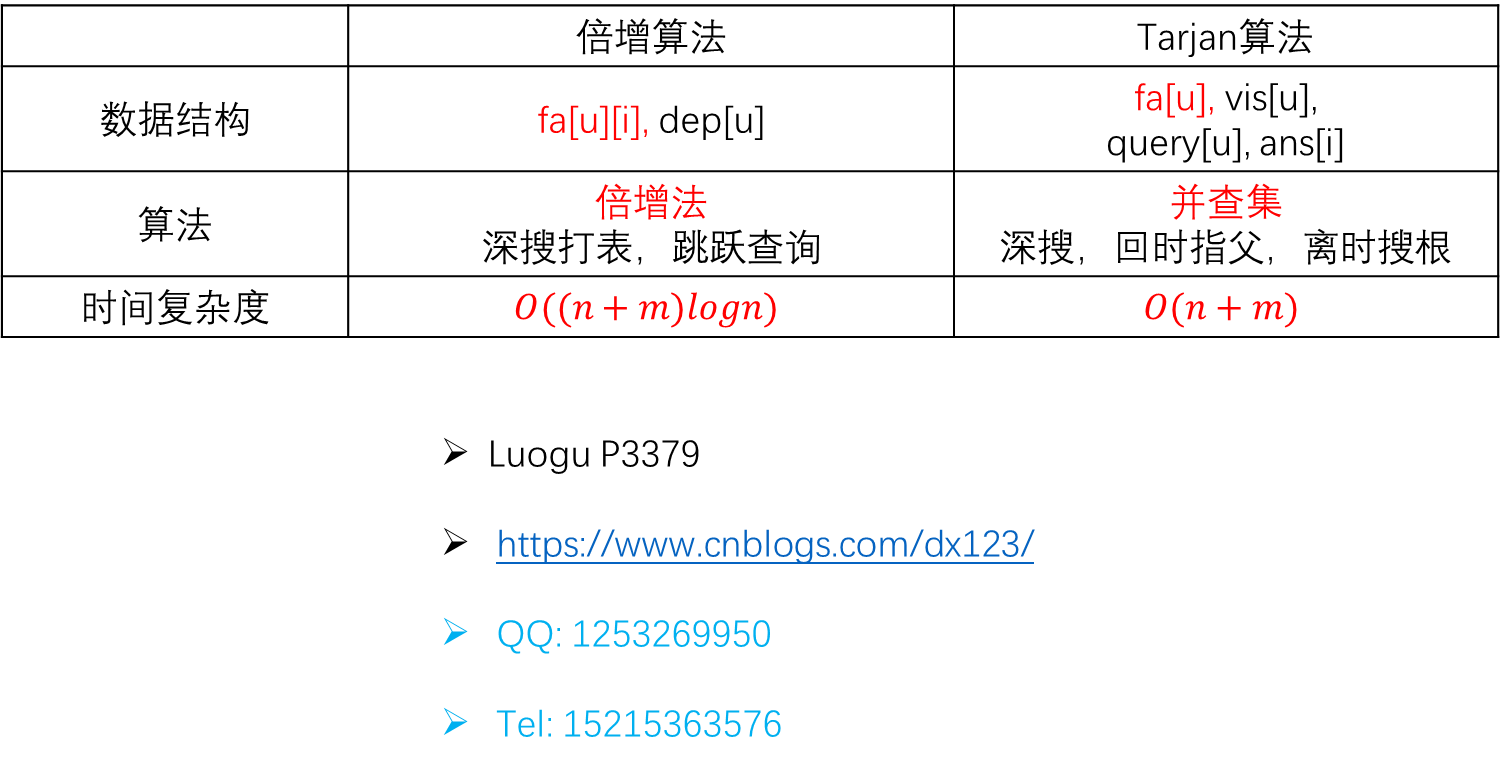
倍增法模版

如果要计算两个点的树上距离使用这个模版会方便点，复杂度\(O((m+n)*logn)\)

/**   - swj -
   *         
　　　　　 ／＞_____フ
　　　　　 | 　_　 _|
　 　　　 ／`ミ _x ノ
　　 　 /　　　 　 |
　　　 /　  ヽ　　 ?
　／￣|　　 |　|　|
　| (￣ヽ＿_ヽ_)_)
　＼二つ
 
**/
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
int n,q;
vector<int>vct[N];
int dep[N],fa[N][20];//dep存u点的深度，fa存从u点向上跳2的i次方层祖先节点

void dfs(int u,int father){
    dep[u]=dep[father]+1;
    fa[u][0]=father;  ////init跳1步
    for(int i=1;i<=17;i++) fa[u][i]=fa[fa[u][i-1]][i-1];
    for(auto v:vct[u]) if(v!=father) dfs(v,u);
}
int lca(int u,int v){
    if(dep[v]>dep[u]) swap(u,v);
    ////先跳到同一层
    for(int i=17;i>=0;i--) if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
    if(u==v) return u;
    for(int i=17;i>=0;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
    return fa[u][0];
}
int dist(int u,int v){ return dep[u]+dep[v]-2*dep[lca(u,v)];}

signed main()
{
   
  //如果没有说明根节点要先找根节点
//求根节点，看哪个节点没有父节点就是根节点-----   
 //输入相关数据，
//-------------------------------
    dfs(head,0);//从根节点开始搜索
    return 0;       
}

tarjan法模版

// 2.0s
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;

const int N=500005,M=2*N;
int n,m,s,a,b;
vector<int> e[N];
vector<pair<int,int>>query[N];
int fa[N],vis[N],ans[M]; 

int find(int x){
  if(x==fa[x]) return x;
  return fa[x]=find(fa[x]);
}
void tarjan(int x){
  vis[x]=true;//标记x已访问
  for(auto y : e[x]){
    if(!vis[y]){
      tarjan(y);
      fa[y]=x;//回到x时指向x
    }        
  }
  //离开x时找LCA
  for(auto q : query[x]){
    int y=q.first,i=q.second;
    if(vis[y])ans[i]=find(y);
  }
}
int main(){
  scanf("%d%d%d", &n,&m,&s);
  for(int i=1; i<n; i++){
    scanf("%d%d",&a,&b);
    e[a].push_back(b);
    e[b].push_back(a);
  }
  for(int i=1;i<=m;i++){
    scanf("%d%d",&a,&b);
    query[a].push_back({b,i});
    query[b].push_back({a,i});
  }
  
  for(int i=1;i<=N;i++)fa[i]=i;
  tarjan(s);
  for(int i=1; i<=m; i++)
    printf("%d\n",ans[i]);
  return 0;
}