T3

题目：CF1039D You Are Given a Tree。

紫题？也不难啊……蔡老师威武，讲的太好了！

题面一坨，概括一下好受很多。

其实可以把题目转化一下，就是找树中有多少条简单路径的点数 \(node \ge k\)。

假设现在位于 \(fa\) 点，则路径的选取有两种可能：

• 选一个儿子 \(u\) 接到 \(fa\) 上形成一条长度加 \(1\) 的链，继续往上接；
• 选两个儿子 \(u_1\)，\(u_2\) 和 \(fa\) 接起来形成一条长度为两个儿子下面接的链的长度加上 \(1\) 的链，上面重新开一条新链。

像极了儿子和父亲一起打怪，显然生命只有一次，打完就噶掉了。。。

我们不妨站在儿子 \(u\) 的角度看，他的父亲是 \(fa\)，还有许多个兄弟。

其实可能还有第三种情况，就是不需要 \(u\) 出手，他的兄弟有太多太多孩子，紧紧依靠兄弟的儿子就可以把 Boss 打爆。

考虑第其他两种情况，

\(u\) 问老爹：“那个啥，我干不动 Boss，救救我！”
老爹：“等下你哥哥的消息。”

然后战况是：老哥的儿子全部噶完了。。老哥自己还活着，比如此时 \(k=2\)，那么老爹只要和哥一起干就行了，轮不到 \(u\)。那么对于 \(u\) 的兄弟来说，这就是第一种情况。如果 \(k=3\)，那么兄弟、爹、\(u\) 一起上阵就能打败 Boss 了。

观察一下上面的思路，我们可以用一个 \(dp\) 数组来记录每一个节点的信息，最开始时，所有元素都初始化为 \(1\)，因为生命只有一次，不对，是每个节点在拼接时只能用一次。

然后为了完成这种思路，我们可以自底向上更新，由于标号是逆的（自底向上），所以可以采用后序的 \(DFS\)，先递归再给节点编号。

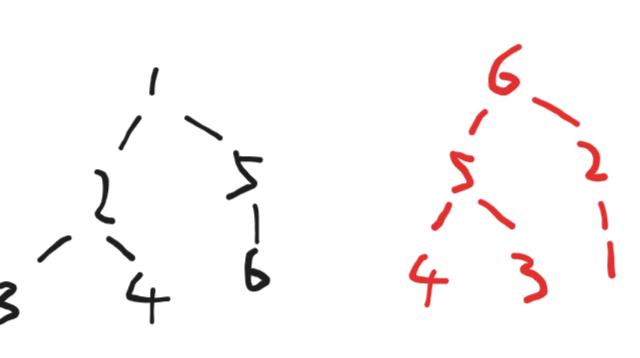
右边的树就是左数编完号后的样子。就好写了，我们按编号从小到大循环，这样必然是按深度从大到小的。

如果这个节点有父亲、父亲还活着、自己也还活着，那么有两种情况：

1. 如果当前的 \(dp_u + dp_{fa} \ge k\)， 就用这个节点和父亲拼接。注意用完后父亲要变成已用状态。
2. 上述条件不成立，那么父亲的 \(dp\) 值就变为最大的那个儿子的值在加 \(1\)。

暴力实现会 T，经过观察我们会发现，第 \(1 \to n\) 优解有很多事重复的。于是考虑根号分治。

当 \(k\) 很小时（\(k \le \sqrt n\)），直接暴力计算每个 \(k\) 的答案。这时候答案变化快，没法偷懒。

当 \(k\) 很大时，答案会断崖式下跌，可以用二分找出每个答案的统治区间，直接批量填答案，省去大量计算。