激光三角测量中的光斑中心定位方法及其特点

激光三角测量中的光斑中心定位方法及其特点

1. 灰度质心法

原理：基于光斑灰度分布，将像素灰度值作为权重计算质心坐标。公式表示为：

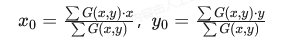
特点：

• 适用于均匀光斑，计算速度快。
• 抗干扰能力差，对光强不均或噪声敏感。

---

2. Hough变换法

原理：通过参数空间投票检测光斑的圆形轮廓，利用光斑几何对称性定位中心。
特点：

• 适用于轴对称或轮廓清晰的圆形光斑，对部分残缺或边缘不连续的光斑仍有效。
• 计算量大，实时性较差，需参数空间离散化。

---

3. 圆拟合法

原理：通过最小二乘法将光斑边缘点拟合成圆，圆心即为光斑中心。
特点：

• 精度高，但抗噪声能力弱，易受随机噪声干扰。
• 适用于高信噪比场景，如实验室环境。

---

4. 高斯曲线拟合法

原理：假设光斑灰度分布符合高斯函数，通过拟合高斯曲面确定中心。
特点：

• 适用于高斯分布光斑，精度较高。
• 计算复杂度高，需迭代优化，实时性受限。

---

5. 改进质心法

原理：

• 平方加权质心法：将灰度值平方作为权重，提升抗噪能力。
• 灰度矩法：结合灰度分布的一阶矩或高阶矩，提高复杂光斑的定位精度。
• 滤波结合质心法：如属性距离加权平均滤波，降低噪声干扰后再计算质心。

---

6. 亚像素算法

原理：在像素级别基础上进一步细分，结合插值或边缘检测（如Hessian矩阵法）提升精度。
特点：

• 分辨率可达亚像素级别（如0.1像素），适用于高精度测量。
• 需处理大量数据，对硬件性能要求高。

---

方法选择建议

• 均匀光斑：优先灰度质心法或改进质心法（实时性要求高）。
• 噪声环境：使用Hough变换或滤波结合质心法。
• 高精度需求：圆拟合法或高斯拟合法。
• 动态测量：优化算法（如随机采样+最小二乘法）提升速度。