动态规划---完全背包

一：完全背包

（一）朴素方法实现完全背包问题（从选0个到选k个将背包填满）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int f[N];    //全局变量，被初始化0
int v[N], w[N];    //对应物品体积和价值

int main()
{
    cin >> n >> m;    //初始化物品数量和背包容积

    for (int i = 1; i <= n; i++)    //初始化数量和价值
        cin >> v[i] >> w[i];        //从i=1开始，将前面流出了哨兵临界位置

    for (int i = 1; i <= n; i++)　　//外层循环是我们的物品
        for (int j = m; j >= v[i]; j--)    //内层循环是我们背包剩余容量，注意：需要添加我们将判断条件提到这一步当中，保证剩余容量大于当前物品的体积
            for (int k = 0; k*v[i] <= j;k++)
                f[j] = max(f[j], f[j - k*v[i]] + k*w[i]);    //对应不选和选

    cout << f[m] << endl;
    system("pause");
    return 0;
}

朴素算法，使用了3层循环，其中最内层循环中k值从0直到装满背包剩余空间位置。上面算法的时间复杂度为O(nW^2)

（二）01与完全推导

1.01背包

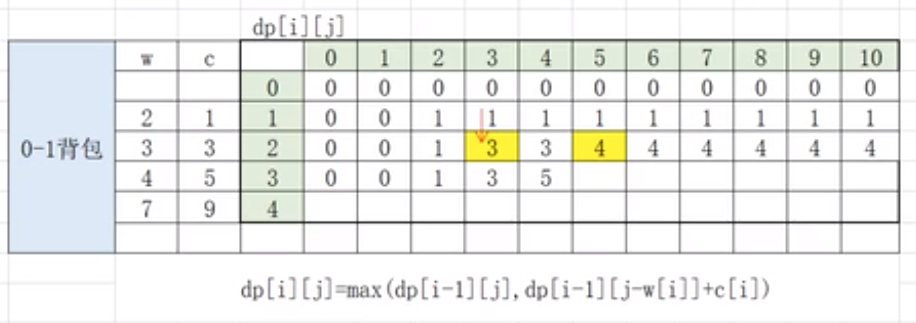
上面是01背包问题的推导列表，用来做比较的是i-1即上一个物品。

从我们上一篇01背包的理解，可以知道第i层的值只与第i-1有关，所以我们可以对dp数组进行压缩处理。https://www.cnblogs.com/ssyfj/p/13624035.html

因为我们用到了上一条的旧数据，所以我们需要进行逆向推导，参考我们01背包问题中j的迭代范围可以知道：

for (int j = m; j >= v[i]; j--)

2.完全背包

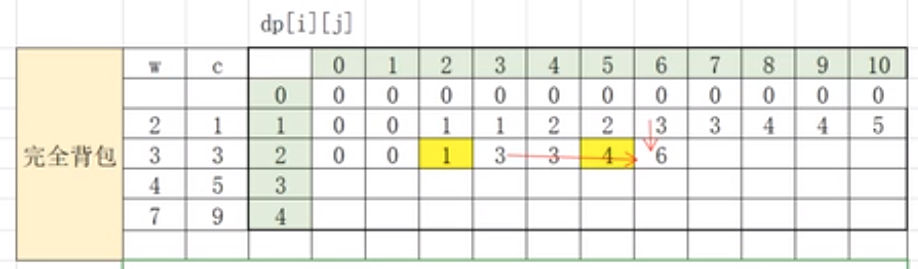
上面是完全背包的推导，当不选时，用到上一个i-1做比较，当选的时候是使用本物品i作为对比。

例如：背包容量为6时，我们选择i=2时，若是不选，则为dp[i-1][j]=3,选择的时候k=1,2可以用dp[i][j-w[i]]+c[i]计算为6即可。

分析01背包的空间压缩，我们对完全背包尝试进行压缩空间处理

 

可以知道我们是使用了本条数据中的新数据进行推导的，我们需要按照顺向进行推导求得前面数据，然后更新后面值即可。

3.以上推导中虽然01背包和完全背包的状态推导方程是完全一样的，但是推到的方向是完全相反的。 

（三）优化后完全背包实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int f[N];    //全局变量，被初始化0
int v[N], w[N];    //对应物品体积和价值

int main()
{
    cin >> n >> m;    //初始化物品数量和背包容积

    for (int i = 1; i <= n; i++)    //初始化数量和价值
        cin >> v[i] >> w[i];        //从i=1开始，将前面流出了哨兵临界位置

    for (int i = 1; i <= n; i++)
        for (int j = v[i]; j <= m; j++)    //注意：需要添加我们将判断条件提到这一步当中，保证剩余容量大于当前物品的体积
                f[j] = max(f[j], f[j - v[i]] + w[i]);    //对应不选和选

    cout << f[m] << endl;
    system("pause");
    return 0;
}