动态规划---01背包问题

补充（一）01背包

补充（二）：状态转移

（一）绘制状态转移方程推导图解

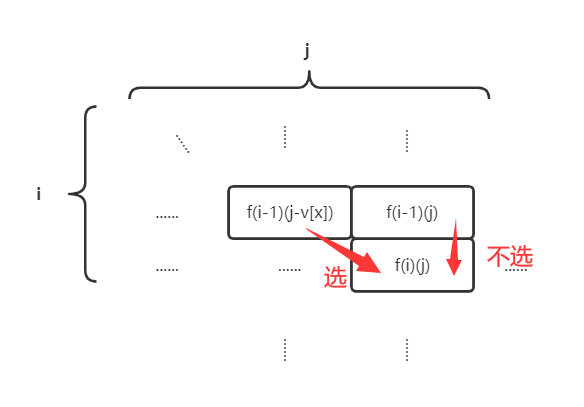
注意：回溯过程中，j表示的是背包剩余容量。

（二）根据推导图解找状态转移方程时，按逆向思维来找

1.不选第i个物品时，f[i][j] = f[i - 1][j]　　其中i - 1表示上一个物品，j表示物品空间剩余位置。

2.选择第i个物品时，f[i][j] = f[i - 1][j - v[i]]　　其中i - 1表示上一个物品的基础上，我们选择了第I个物品后的剩余空间位置时j - v[i]

（三）找初始值时，可以逆向思维寻找

只有最后结果f[0][0] = 0结束

一：01背包https://www.cnblogs.com/mfrank/p/10533701.html 

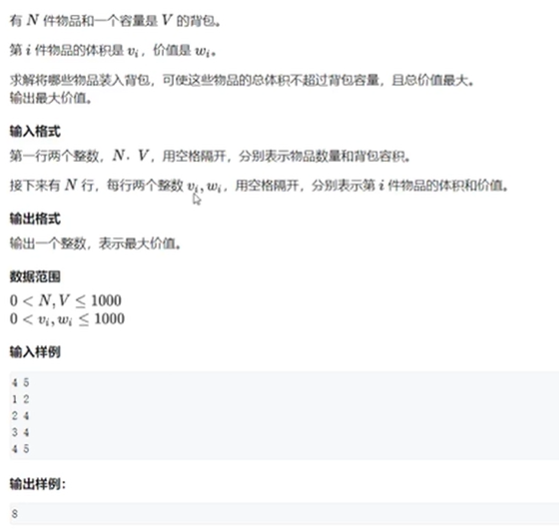
（一）动态规划入手

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int f[N][N];    //全局变量，被初始化0
int v[N], w[N];    //对应物品体积和价值

int main()
{
    cin >> n >> m;    //初始化物品数量和背包容积

    for (int i = 1; i <= n; i++)    //初始化数量和价值
        cin >> v[i] >> w[i];        //从i=1开始，将前面流出了哨兵临界位置
    
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (j >= v[i])        //注意：需要添加判断条件，保证剩余容量大于当前物品的体积
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);    //对应不选和选

    cout << f[n][m]<<endl;
    system("pause");
    return 0;
}

注意：我们使用了动态规划，使用的判断条件是j>=v[i],使得最终结果满足了我们要求的物品体积小于等于背包容量

（二）优化系统，节约空间

分析状态转移推导图，我们每次的f[i][j]只与上一层i-1有关，所以我们不需要使用二维空间进行存储数据，可以进一步压缩为一维空间。

同时在迭代过程中，发现f[i][j]与第i层左侧有关，所以我们在迭代过程中，不能从左向右进行，否则会覆盖掉后面需要的数据，我们需要从右向左迭代。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int f[N];    //全局变量，被初始化0
int v[N], w[N];    //对应物品体积和价值

int main()
{
    cin >> n >> m;    //初始化物品数量和背包容积

    for (int i = 1; i <= n; i++)    //初始化数量和价值
        cin >> v[i] >> w[i];        //从i=1开始，将前面流出了哨兵临界位置
    
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)    //注意：需要添加我们将判断条件提到这一步当中，保证剩余容量大于当前物品的体积
                f[j] = max(f[j], f[j - v[i]] + w[i]);    //对应不选和选

    cout << f[m]<<endl;
    system("pause");
    return 0;
}

（三）初始化问题

我们声明了全局变量f[N],位于静态区，被全部初始化为0。所以我们在迭代过程中结果正确。

1.正向迭代（在正向迭代过程中，我们只是需要将f[0]设置为0即可）---最终结果在f[k]位置

f[0] = 0 => f[0+v[0]] = w[0] => ....

2.反向迭代（在反向迭代过程中，我们最终结果在f[m]处，我们只需要相对于正向迭代添加一个偏移量m-k,将f[m-k]=0即可，后面迭代是一样的。所以我们最好将全部初始化为0）

f[m - k] = 0 => f[m - k + v[0]] = w[0] => ......

3.所以我们如果要确保所有状态都是从0转移过来，我们需要将f[0]初始化0，其他为-INF，如果从其它转移，结果必为-INF