最大红矩形---栈的应用

一：问题描述

有一个 n*m 的棋盘，棋盘上的每个点都是红的或绿的。
你需要找出一个面积最大的矩形区域，使得其中没有绿的格子。

（二）输入输出

输入格式

第一行 2 个正整数 n,m，描述棋盘尺寸。

接下来 n 行描述这个棋盘，每行 m 个字符，每个字符为 . 或 X，其中 . 表示这个位置是红色的，X 表示这个位置是绿色的。

4 5　　　　　　//输入行列

　　　　　　　　//下面输出矩阵信息，“.”表示红色，“X”表示绿色
.....
XXXXX
.X...
.....　　　　　//这里的红色矩阵是最大矩阵，面积为6

输出格式

一行一个整数，表示最大面积。　　

6        //数据最大面积为6

二：思路解析

（一）是对前面的直方图的扩展

（二）处理获取的数据---将二维数据按照直方图中一维处理

1.处理我们获取的二维数据

0.单独考虑某一列数据，进行举例

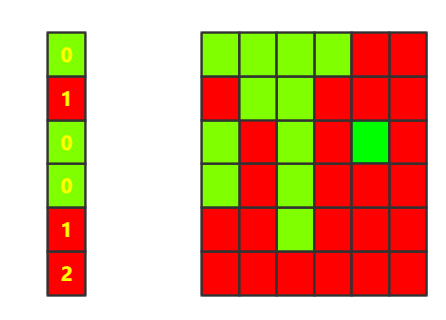
我们需要求最大红矩形，所以对于绿色行皆是0，
对于第一列为绿色，高度为0
对于第二列是红色，且上面一个方块为绿色，所以高度为1（0+1），
对于第三第四列皆为绿色，为0。
对于第五列，为红色，上面为绿色故高度为1（0+1），
对于第六列，为红色，且上面为红色，故高度为上面方块的高度+1

1.原始图形

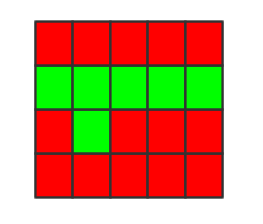
2.处理第一行，获取该行向上的高度（都是红色，且相连）

3.处理第二行，因为该行都是绿色。故全部为0

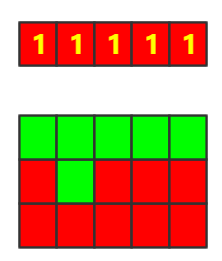
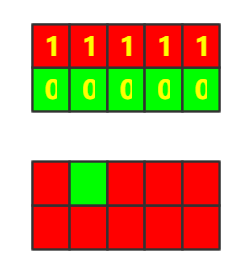
3.处理第三行，若是为红色则高度为上一行高度加一，否则若是绿色则设置为0

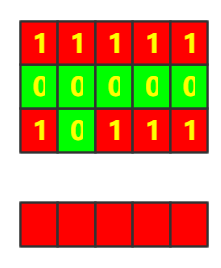
4.处理第四行，若是为红色则高度为上一行高度加一，否则若是绿色则设置为0

2.对每一行进行遍历，求取每一行最大矩形，最终即可获取这个最大红矩形

三：代码实现

#include <iostream>
#include<stack>

using namespace std;

#define MAXLEN 1050

char CRect[MAXLEN][MAXLEN] = {
    { '.', '.', '.', '.', '.', '.' },
    { 'X', 'X', 'X', 'X', 'X', 'X' },
    { '.', 'X', '.', '.', '.', '.' },
    { '.', '.', '.', '.', '.', '.' },
};

int IRect[MAXLEN][MAXLEN];
int n=4, m=5;

int getMaxRect(const int* const height,int len)
{
    stack<int> stk;
    int Max_area = 0, Loc_area,i,h,w;
    for (int i = 0; i < len; i++)
    {
        if (stk.empty() || height[i]>height[stk.top()])
            stk.push(i);
        else
        {
            while (!stk.empty() && height[i] < height[stk.top()])    //出栈元素并求最大矩形
            {
                h = height[stk.top()], stk.pop();
                w = i - 1 - (stk.empty() ? -1 : stk.top());
                Loc_area = h*w, Loc_area > Max_area ? Max_area = Loc_area : Max_area;
            }
            stk.push(i);
        }
    }

    while (!stk.empty())    //处理栈非空情况
    {
        h = height[stk.top()], stk.pop();
        w = len - 1 - (stk.empty() ? -1 : stk.top());
        Loc_area = h*w, Loc_area > Max_area ? Max_area = Loc_area : Max_area;
    }

    return Max_area;
}

int main()
{
    int Max_area = 0,i,j;

    for (i = 0; i < n; i++)    //先处理原始数据
    {
        for (j = 0; j < m; j++)
        {
            if (CRect[i][j] == 'X')
                IRect[i][j] = 0;
            else if (i == 0 && CRect[i][j] == '.')
                IRect[i][j] = 1;
            else
                IRect[i][j] = IRect[i - 1][j] + 1;
        }
    }

    for (i = 0; i < n; i++)    //处理每一列数据，获取最大红矩形
    {
        j = getMaxRect(IRect[i], m);
        Max_area = Max_area > j ? Max_area : j;
    }

    cout << "Max rect area:" << Max_area << endl;

    system("pause");
    return 0;
}