直方图最大矩形面积---栈的应用

一：题目

求一个直方图的最大矩形面积：如图

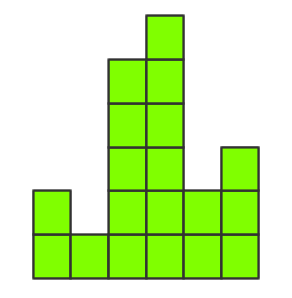
高度：{ 2, 1, 5, 6, 2, 3 }

其可能出现的矩形：

1.每一列都是一个矩形

......

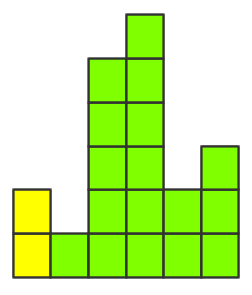
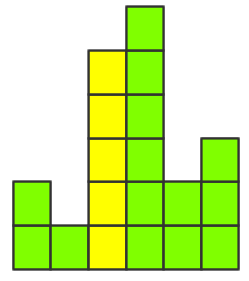2.多列进行组合，可以形成一个较大矩形

......

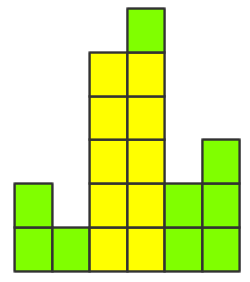
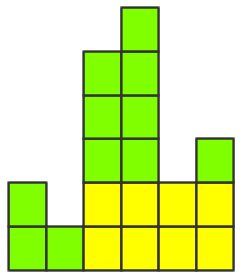其中最大矩形即2中第一个矩形，大小为10

二：暴力求解 

 理解较为容易，实现较为简单，但是时间复杂度可能有点大

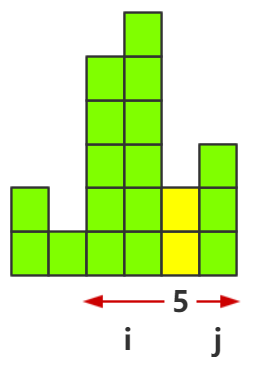
循环遍历每一列（该列高度为当前矩形高度），同时声明两个变量i,j分别向左右寻找卡位点（即可获得当前矩形的宽度）

对于每一列都可以获得一个当前最大矩形，比较各个矩形面积，即可获取到全局最大矩形面积

for 循环每一列
    for i向左循环找卡位点
        ...
    for j向右循环找卡位点
        ...
    当前最大矩形面积=高度*宽度
    if(比较当前矩形面积和全局最大矩形面积)
        进行修改全局最大矩形面积

时间复杂度大约为O(n²)

三：栈的使用，求解最大矩形面积 

（一）演示说明

1.初始状态

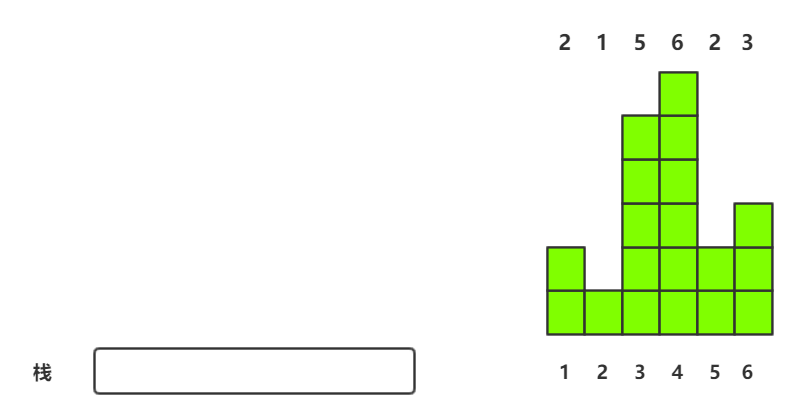
其中栈为M,直方图为H[]={0,2,1,5,6,2,3}　　加0是为了符合上面直方图的序号，避开下标0进行讲解较为方便（但是写代码还是考虑下标0）

2.第一个元素入栈（栈空）

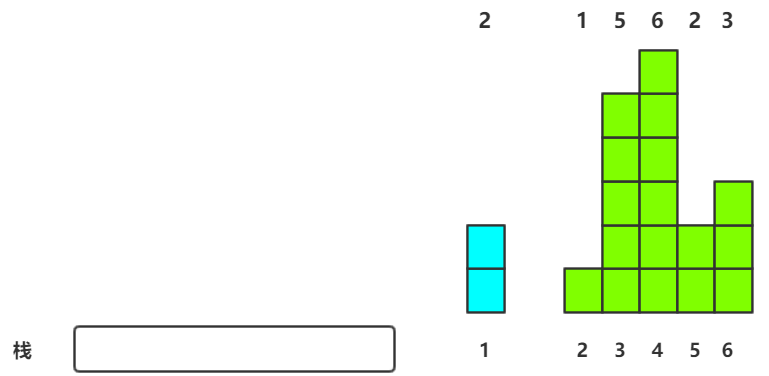
1.栈为空，直接入栈

 

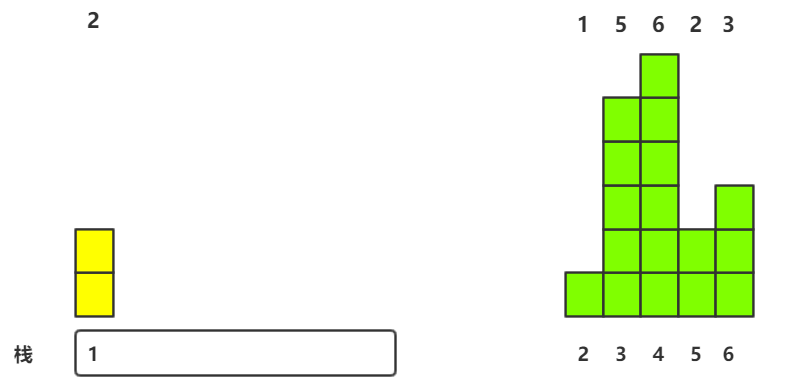
2.第二个元素入栈（即将入栈的元素小于栈顶元素的情况）

因为栈中存在元素，故用栈顶元素H[M.top()]---2与H[2]---1进行比较，发现栈顶元素大于即将入栈的元素

则先考虑栈顶元素（因为栈始终要保持递增，故该列左侧小于该列，右侧--即将入栈元素也小于该列，皆为卡位点），
对其该列求最大矩形面积（高为该列高度H[M.top()],宽为卡位点序号相减再减一），之后将栈顶进行出栈M.pop()，
之后将即将入栈的元素继续与新的栈顶元素进行比较，直到栈空，或者栈顶元素小于自己则入栈。

1.先求栈顶元素的最大矩形---高2宽1=2
2.将该元素出栈
3.栈为空则将元素第2列直接入栈

 

 

3.第三个元素入栈

 

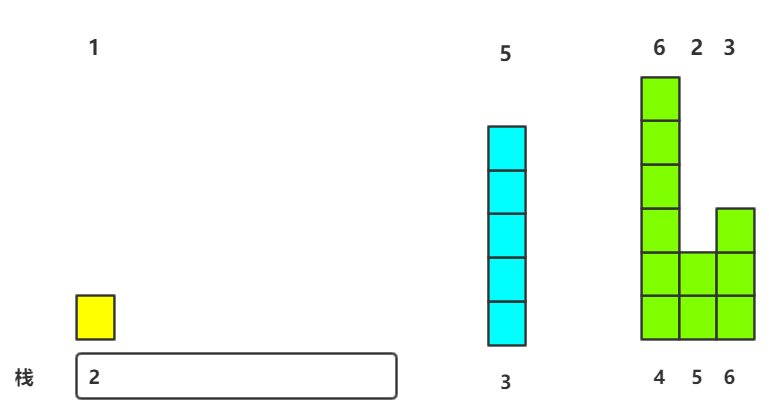
因为即将入栈的元素高度H[3]大于H[M.top()],故直接入栈即可

 

4.第四个元素进栈

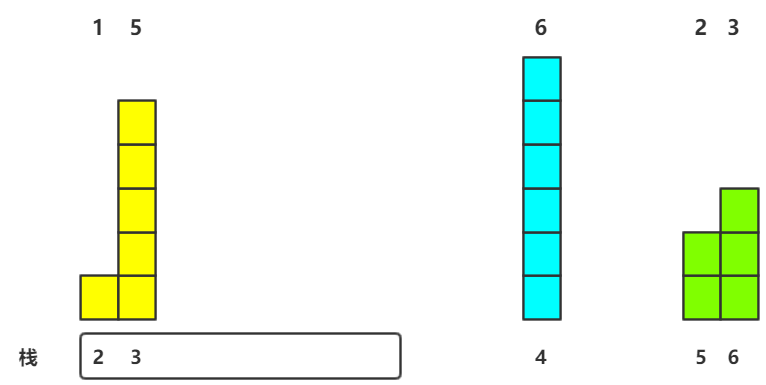
因为即将入栈的元素高度H[3]大于H[M.top()],故直接入栈即可

 

5.第五个元素进栈

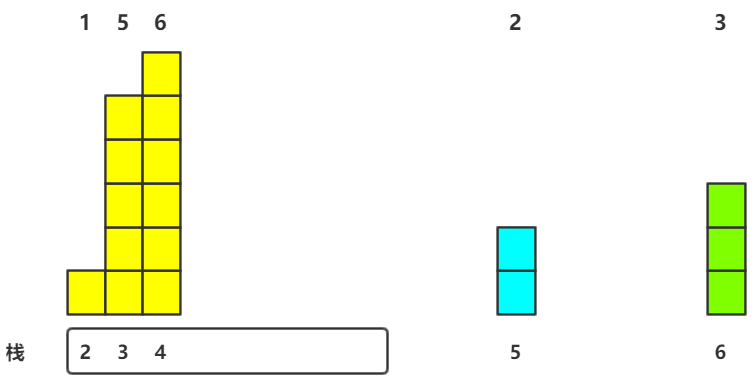
1.H[5]<H[M.top()]，故将栈顶出栈，求其最大矩形面积---高为6，宽为5-3-1=1---面积6

 

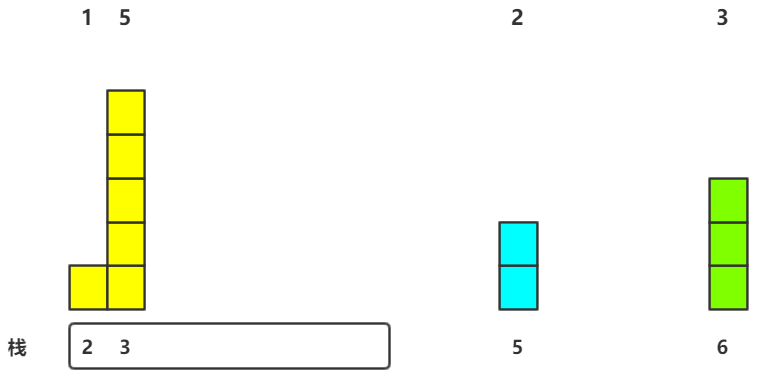
2.因为新的栈顶元素H[M.top()]依旧大于H[5],故同上求新的栈顶元素的最大矩形面积---高为4，宽为5-2-1=2---面积10

 

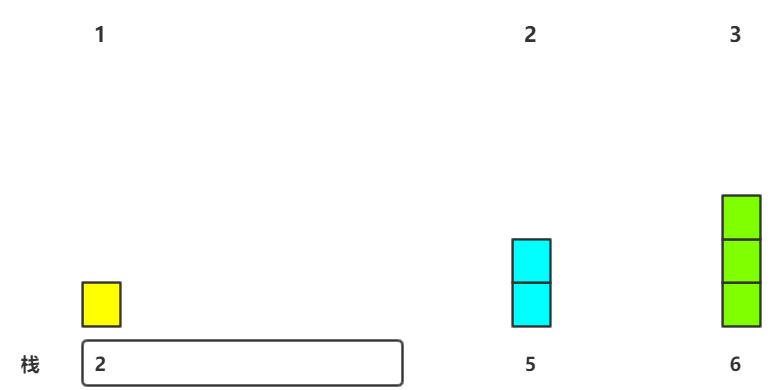
3.因为栈顶元素小H[M.top()]<H[5],故直接入栈

 

6.第六个元素进栈

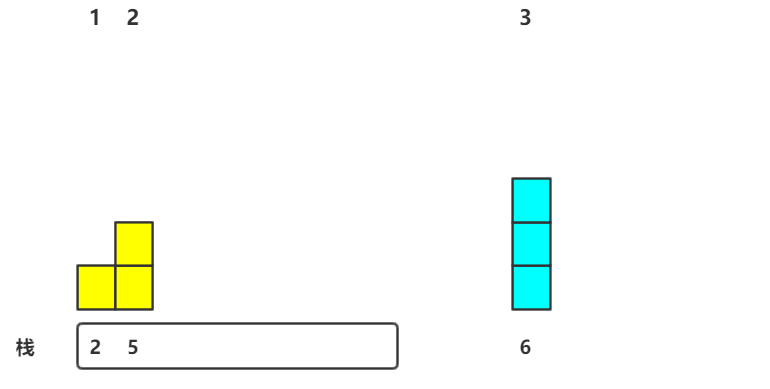
因为栈顶元素小H[M.top()]<H[6],故直接入栈

 

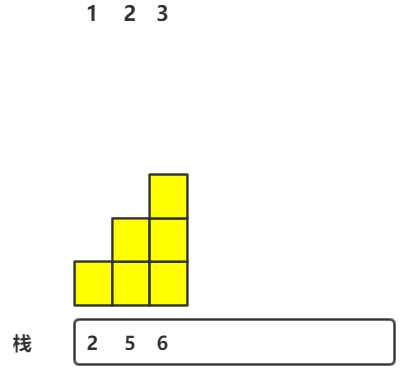
7.最后栈不为空时

依次将栈中元素出栈，求最大矩形面积

1.出栈栈顶元素，高为3，宽为1---面积3

 

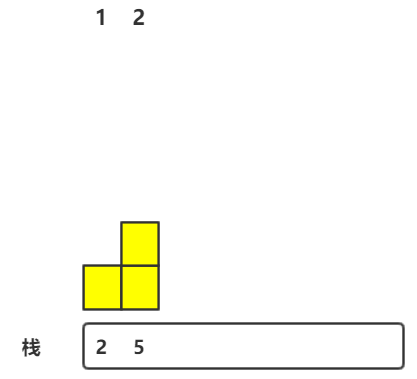
2.出栈栈顶元素，高为2，宽为7-2-1=4（其中7是最右侧哨兵），面积是8

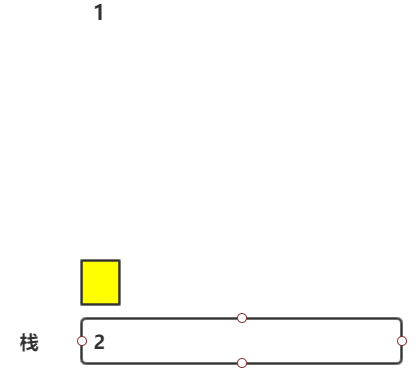
3.出栈栈顶元素，高为1，宽为7-0-1=6（其中7是最右侧哨兵，0是最左侧哨兵），面积是6

8.比较最大矩形面积

为10

（二）代码实现

#include <iostream>
#include<stack>

using namespace std;

#define LEN 6
int height[LEN] = { 2, 1, 5, 6, 2, 3 };        //测试代码    结果为10

int main()
{
    stack<int> stk;
    int Max_area=0,Loc_area,h,w;

    for (int i = 0; i < LEN; i++)
    {
        if (stk.empty() || height[i]>height[stk.top()])
            stk.push(i);
        else
        {
            while (!stk.empty() && height[i] < height[stk.top()])    //出栈元素并求最大矩形
            {
                h = height[stk.top()], stk.pop();
                w = i - 1 - (stk.empty() ? -1 : stk.top());
                Loc_area = h*w, Loc_area > Max_area ? Max_area = Loc_area : Max_area;
            }
            stk.push(i);
        }
    }

    while (!stk.empty())    //处理栈非空情况
    {
        h = height[stk.top()], stk.pop();
        w = LEN - 1 - (stk.empty() ? -1 : stk.top());
        Loc_area = h*w, Loc_area > Max_area ? Max_area = Loc_area : Max_area;
    }

    cout << "Max rect area:" << Max_area << endl;

    system("pause");
    return 0;
}

对于每个元素只需要一次进栈一次出栈，时间复杂度为O(n)

四：启示

学会在算法后面去分析时间复杂度，容易理解的可能时间复杂度会更高。所以去分析每一个算法的复杂度，有利于我们了解一个算法的优点