毛毛虫剖分

毛毛虫剖分

毛毛虫指树上的一条链（虫身）以及与链上节点直接相连的点（虫足）。

涉及一些需要维护一个节点其直接相连节点的信息

其本质是魔改重链剖分

详细的说，步骤差不多是：

• 魔改重链剖分的标号，让其满足我们所需维护的信息。

• 设计数据结构维护信息

• 统计答案

一般的有：保证重链上的点编号连续，保证虫足编号连续，保证虫编号连续，保证子树编号连续等等。

一般的构造方法是：

• 特别处理链顶（牺牲链顶法（doge）），保证除了链顶编号连续
• 给链编号
• 给虫足编号
• 递归虫足

编号顺序由题决定。

部分题目可能需要向上向下各维护一个毛毛虫

下面两个例题的维护方式比较广泛。

轻重边

给定一棵树，支持两个操作

• 先将端点在 \(u\to v\) 路径上的所有边变为白色，然后将这条路径上所有边变为黑色
• 询问 \(u\to v\) 路径上黑色边有多少

边权放到点，翻译一下就是：

• 将 \(u\to lca\to v\) 构成的虫全部变成 \(0\)，除了 \(LCA\) 的父亲
• 将 \(u\to lca\to v\) 整条链（除了 \(lca\)）赋值为 \(1\)

考虑一个魔改的标号

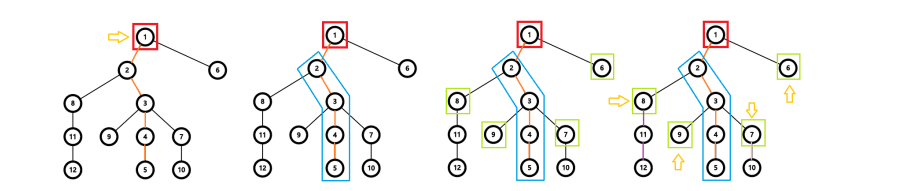
​ ·牺牲链顶，然后不断跳 \(son_u\)，将整棵重链标号。

然后再从链顶开始不断跳虫足（特征：这时候虫足还未标号）标号

标号完成后统一递归虫足处理。

我们维护 \(bl_u,br_u\) 表示 \(u\) 的虫足编号（也就是往下的虫足，往上不考虑）

维护 \(clik_u\) 表示从这个点开始的下一个点编号。特别对链顶进行处理。注意这里得提前预处理 \(1\) 的标号

void divide(int u,int tp){
    top[u]=tp;clik[u]=idx+1;
    for(int v=son[u];v;v=son[v]){
        dfn[v]=++idx;clik[v]=idx+1;top[v]=u;clik[v]=idx+1;
    }
    for(int v=u;v;v=son[v]){
        bl[v]=idx+1;
        for(auto t:e[v])if(!dfn[t])dfn[t]=++idx;
        br[v]=idx;
    }
    for(int v=u;v;v=son[v]){
        for(auto t:e[v])if(!top[t])divide(t,t);
    }
}

然后我们考虑修改。其实很简单，我们将一条链的 \(top\) 特别处理，然后将 \(clik[top]\to u\) 整体处理。

至于虫足，一条链的虫足根据编号连续直接区间修改即可。（\(u\to v\)，虫足 \(bl_u\to br_v\)）

注意 \(lca\) 处需要特别处理。跳链的时候，跳上去之后的重儿子需要特别处理。

void change(int u,int v){
    int t=lca(u,v);
    seg::upd(dfn[t],dfn[t],0);seg::upd(bl[t],br[t],0);
    if(son[t])seg::upd(dfn[son[t]],dfn[son[t]],0);
    for(auto x:{u,v}){
        int lst=0;
        while(top[x]!=top[t]){
            seg::upd(bl[top[x]],br[x],0);//虫足
            if(son[x])seg::upd(dfn[son[x]],dfn[son[x]],0);//特判跳上来之后得清
            seg::upd(clik[top[x]],dfn[x],1);//整体虫身赋值
            if(lst)seg::upd(dfn[lst],dfn[lst],1);//上条链的顶部
            lst=top[x];x=fa[top[x]];
        }
        if(x!=t){
            seg::upd(bl[son[t]],br[x],0);//注意不改lca
            if(son[x])seg::upd(dfn[son[x]],dfn[son[x]],0);
            seg::upd(clik[t],dfn[x],1);
        }
        if(lst)seg::upd(dfn[lst],dfn[lst],1);
    }
}

查询就很简单了。

int query(int u,int v){
    int t=lca(u,v),res=0;
    for(auto x:{u,v}){
        int lst=0;
        while(top[x]!=top[t]){
            /*不含topx的答案，所以说毛毛虫的topx要单独处理*/
            res+=seg::ask(clik[top[x]],dfn[x]);
            if(lst){
                res+=seg::ask(dfn[lst],dfn[lst]);
            }
            lst=top[x];x=fa[top[x]];
        }
        if(x!=t)res+=seg::ask(clik[t],dfn[x]);
        if(lst)res+=seg::ask(dfn[lst],dfn[lst]);
    }
    return res;
}

毛毛虫剖分的本质是通过特殊点重标号手段，使得在牺牲 \(top\) 的情况下保证虫身

这个剖分还有一些性质：

• 一个子树最多被剖分为三个不交区间（当前点所在重链链底到自己的编号，以及虫足编号，然后就是自己第一个虫足进去之后的编号……，细节比较多）

祖先

支持三个操作：

• 单点加
• 子树加
• 求 \(\sum_{i=1}^n\sum_{j=i+1}^n[u=lca(i,j)]a_ia_j\)

设 \(s_u\) 为子树点权和，容易发现第三个操作的答案就是：

\[\frac{s_u^2-\sum_{v}s_v^2-a_u}{2} \]

所以我们需要设计一个毛毛虫，支持查询某个点的虫足子树点权和的平方和，某个点的子树点权和，以及维护每个点的点权。

显然我们只需要保证：

• 虫足编号连续
• 知道每个点的编号
• 子树编号连续

可以再次魔改毛毛虫标号。

注意到这里我们只需要知道一个点的虫足，但是需要让子树编号连续。所以我们可以牺牲一整条链虫足编号连续的优点。

很简单。

我们先给重链自顶向下标号，然后自底向上给轻儿子标号，一个点的轻儿子编号完成后直接递归处理。这样可以保证除了子树根节点，其他点编号连续。

void divide(int u,int tp){
    top[u]=tp;tl[u]=idx+1;int lst=u;
    for(int v=son[u];v;lst=v,v=son[v]){
        dfn[v]=++idx;rew[idx]=v;tl[v]=idx+1;top[v]=u;
    }
    for(int v=lst;v!=fa[u];v=fa[v]){
        bl[v]=idx+1;
        for(auto t:e[v])if(!dfn[t])dfn[t]=++idx,rew[idx]=t;
        br[v]=idx;
        for(auto t:e[v])if(!top[t])divide(t,t);
        tr[v]=idx;
    }
}

处理修改是简单的。我们首先用一个树状数组维护一下点权，然后用线段树维护 \(s\)。

对于 \(s\)，第一个修改点权相当于修改该点到根的一条链。第二个修改相当于是子树内自己加上 \(siz\)，子树外也是该点到根节点相当于加上 \(siz·k\)。

void chglik(int u,int k){
    a[u]+=k;int lst=0;
    while(top[u]){
        if(lst)seg::upd(dfn[lst],dfn[lst],k,1);//特殊处理父亲
        seg::upd(tl[top[u]],dfn[u],k,1);//一条链
        lst=top[u];u=fa[top[u]];
    }
    if(lst)seg::upd(dfn[lst],dfn[lst],k,1);
}
void chgson(int u,ull k){
    BIT::chg(dfsn[u],dfsn[u]+siz[u]-1,k);
    seg::upd(tl[u],tr[u],k,0);a[u]-=k*siz[u];
    chglik(u,k*siz[u]);
}
ull query(int u){
    ull su=seg::ask(dfn[u],dfn[u]);
    su-=seg::ask(bl[u],br[u]);
    if(son[u])su-=seg::ask(dfn[son[u]],dfn[son[u]]);
    ull res=BIT::ask(dfsn[u])+a[u];
    su-=res*res;
    return su>>1;
}

毛毛虫剖分的过程中需要特别处理重儿子。

关于线段树部分：

维护 \(vals=\sum s_i\)，\(valqs=\sum s_i^2\)，\(szs=\sum siz_i\)，\(szqs=\sum siz_i^2\)，\(vmsz=\sum s_i·siz_i\)，\(len=r-l+1\)。

同时维护两个懒标记 \(lzsf,lzsz\) 分别表示单点修改和子树修改。

其中 \(szs,szqs,len\) 是定值，可以建树的时候维护好。注意到两个懒标记互不干扰，所以可以任意维护。

对于单点的 \(s\) 增加 \(k\)。

根据 \((s+k)^2=s^2+k^2+2sk\)，可以得到：

\[\begin{aligned} lzsf&\leftarrow lzsf+k\\ valqs&\leftarrow len·k^2+valqs+2vals·k\\ vals&\leftarrow len·k+vals\\ vmsz&\leftarrow vmsz+szs·k\\ \end{aligned} \]

对于整体的子树增加 \(k\)，相当于单点 \(s\) 增加了 \(siz·k\)，\((s+siz·k)^2=s^2+2s·siz·k+k^2siz^2\)可以得到：

\[\begin{aligned} lzsz&\leftarrow lzsz+k\\ valqs&\leftarrow valqs+szqs·k^2+2vmsz·k\\ vals&\leftarrow vals+szs·k\\ vmsz&\leftarrow szqs·k \end{aligned} \]

询问的是 \(valqs\)。