Theta-star算法代码实现

A*和Theta*算法

A*搜索过程中仅考虑网格路径（路径只能是栅格的边或对角线）;Theta*搜索和平滑操作交错执行（路径可以是任意直线，只要**视线检

查**通过），相当于在线平滑。

路径搜索

评估函数f(n)=g(n)+h(n),表示经过节点N完成路径的代价，其中：

g(n)为起点S到当前节点 n 的实际代价；

h(n)为从当前节点 n 到终点E的估算代价（启发式函数)。

算法的目标是始终扩展 f(n) 最小的节点。

代码演示

变量说明

open_set = []
heapq.heappush(open_set, (self._heuristic(start_idx, end_idx) / self.v_g_est, start_idx))
came_from = {}
g_score = defaultdict(lambda: float('inf'))
g_score[start_idx] = 0

S = (227, 612, 2)；E = (27, 37, 2)。

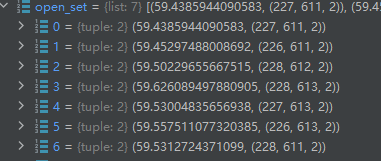
open_set=[f(n),id]; heapq库实现的优先队列；根据节点的优先级f(n)进行排序；每次迭代，算法总是从 open_set 中取出 f_score 最小的那个节点。

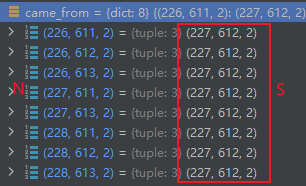
came_from：字典，存储了每个节点的前一个节点（父节点）。键是子节点，值是其父节点。
一个节点可能是多个节点的父节点、但是每个节点至多只有一个父节点。（字典的每个键（子节点）都只对应一个值（父节点），因此

当前最优会被更优覆盖。）

根据父节点的更新规则，假设B的父节点是A，更新为B的父节点是C：'B': 'A'--->'B': 'C'，
parent_idx = C ; neighbor_idx = B
说明：

从起点S到B的最短时间：g_score[neighbor_idx] 大于 从起点 S到C的时间（g_score[parent_idx=B]） + C到B的时间 （distance_BC / ground_speed）；
而 g_score[neighbor_idx] 是之前使用A作为父节点计算的，= 从起点 S到A的时间（g_score[parent_idx=A]） + A到B的时间 （distance_AC / ground_speed）；

需要注意：A的父节点为B仅仅表示从起点到A的最优路径是S-B-A,但是S-B的路径还需要看B的父节点是谁。

# 如果可见，尝试直接连接，并计算新路径代价
distance = self._heuristic(parent_idx, neighbor_idx)
ground_speed = self._calculate_ground_speed(parent_idx, neighbor_idx)
tentative_g_score = g_score[parent_idx] + distance / ground_speed
if tentative_g_score < g_score[neighbor_idx]:
    came_from[neighbor_idx] = parent_idx

例子：
came_from = {
'B': 'A', # 从A到B
'C': 'B', # 从B到C
'D': 'B', # 从B到D
'E': 'C' # 从C到E
}

算法实现

从起点S开始,f(S)=g(S)+h(S)=0+h(S), 即：起点S到终点E的估算代价，open_set = [f(S),S];

came_from为空。

第一次迭代

迭代open-set,取出目前f最小的点（即移除，这是heapq的特性），Start_id --> C_id。

依次计算8个邻居N的g_score,记录邻居N_{i}_S的父节点为S;open_set 添加 [f(N_i),i],f_score最小的排在首位;

计算时通过came_from查询S的父节点,为None，不用视线检查，退化为A*的邻居检查。

第二次迭代 ： 迭代计算S的最优邻居N_{1}S的邻居N_N1。

取出目前f_score最小的点N_{1}_S --> C_id:

依次计算8个邻居N的g_score；计算时通过came_from查询C_id的父节点，发现是Start_id，需要进行视线检查（LoS）;

核心思路为： 如果C_id的父节点Start_id 和 C_id的邻居节点 N_{i}_N1 之间无障碍物；则直接计算 **从父节点到邻居节点的

f_score**;将score更小的点并加入队列。如果视线检查不通过，则退化为A*.

例如，C_id的8个邻居节点中，有三个通过视线检查，直接成为了{C_id的父节点Start_id}的子节点，和C_id同等地位。

![image](https://img2024.cnblogs.com/blog/2712165/202509/2712165-20250922165917549-26520440.png)

if parent_idx is not None and self._is_line_of_sight_clear(parent_idx, neighbor_idx,
                                                           check_wind_change):
    # 如果可见，尝试直接连接，并计算新路径代价
    distance = self._heuristic(parent_idx, neighbor_idx)
    ground_speed = self._calculate_ground_speed(parent_idx, neighbor_idx)

    tentative_g_score = g_score[parent_idx] + distance / ground_speed

    if tentative_g_score < g_score[neighbor_idx]:
        came_from[neighbor_idx] = parent_idx
        g_score[neighbor_idx] = tentative_g_score
        heapq.heappush(open_set,
                       (g_score[neighbor_idx] +
                        self._heuristic(neighbor_idx, end_idx) / self.v_g_est, neighbor_idx))

中间迭代 ：

不断遍历openset中f_score最小的点作为current_idx，并计算C_id的8个邻居节点和C_id的父节点是否通过视线检查，将通过视线检查的点加

入came_from 和openset。

随着迭代的进行，搜索范围不断扩大，open_set 中的节点会越来越接近终点 E。

路径收敛：由于启发式函数 h(n) 的存在，算法会倾向于向终点方向扩展。通过 Theta* 的视线检查，路径会尽量拉直，避免不必要的拐点。

找到终点：当某个被取出的 current_idx 正好等于 end_idx 时，if current_idx == end_idx 条件成立，path_found 被设为 True，搜索循环结束。

迭代结束 路线重建

从end_idx开始，从came-from字典中逆向重建路径。

只要当前节点 current 是 came_from 字典中的一个键（即它有一个父节点），循环就继续执行。

• 将当前节点的坐标添加到 path 列表中。
• 将 current 的值更新为它的父节点。
• 。。。。。。。
  最后 添加起点坐标，反转路径。

# 重建路径 (复用 A* 逻辑)
path = []
current = end_idx
while current in came_from:
    path.append(voxel_idx_to_utm(current))
    current = came_from[current]
path.append(voxel_idx_to_utm(start_idx))
path.reverse()

补充2025.9.23

实验发现一致情况：current_idx的邻居neighbor_idx和current_idx的父节点parent_idx如果是同一个点，应该跳过。