梯度方差的概念

梯度方差的概念

内容

在深度学习中，梯度方差（Gradient Variance） 是一个关键概念，它直接影响模型的训练稳定性和收敛速度。以下用通俗的语言和实际例子解释它的含义、作用及影响。

---

1. 什么是梯度方差？

• 定义：
  梯度方差表示 不同批次数据计算出的梯度之间的波动程度。
  如果每个批次（batch）的梯度差异很大，则梯度方差高；反之方差低。

• 类比理解：
  假设你想估算全校学生的平均身高：

  • 高方差：每次随机选5个学生，算出的平均值忽高忽低（波动大）。
  • 低方差：每次随机选100个学生，算出的平均值更稳定。

• 数学表示：
  梯度方差是统计量：
  [
  \text{Var}(\nabla \theta) = \mathbb{E}\left[ (\nabla \theta - \mathbb{E}[\nabla \theta])^2 \right]
  ]
  其中 (\nabla \theta) 是某个批次数据的梯度。

---

2. 梯度方差如何影响训练？

梯度方差直接影响参数更新的稳定性，具体表现如下：

(1) 高梯度方差（如小批量或单样本）

• 现象：
  每个批次的梯度方向差异大（“有的批次说参数该往东走，有的说该往西走”）。
• 影响：
  • 参数更新不稳定，损失函数震荡剧烈（如下图左）。
  • 需要更小的学习率来避免“跑偏”，导致收敛速度慢。
  • 可能跳出局部极小值，提升模型泛化能力（某种程度是优点）。

(2) 低梯度方差（如大批量或全量数据）

• 现象：
  梯度方向一致性强，更新方向更准确。
• 影响：
  • 参数更新稳定，损失函数平滑下降（如下图右）。
  • 允许更大的学习率，加快收敛。
  • 可能收敛到尖锐的局部极小值，泛化性能可能下降。

---

3. 梯度方差的来源

梯度方差主要由以下因素决定：

(1) 批次大小（Batch Size）

• 小批量（如 batch_size=32）：
  每个批次的数据量少，梯度估计噪声大 → 方差高。
• 大批量（如 batch_size=1024）：
  更多数据平滑了噪声 → 方差低。

(2) 数据多样性

• 数据分布越复杂（如不同类别差异大），梯度方差越高。
• 数据噪声多（如标注错误），也会增加方差。

(3) 模型复杂度

• 复杂模型（如深层神经网络）的梯度计算涉及更多非线性变换，可能导致梯度方差更高。

---

4. 实际例子

假设用随机梯度下降（SGD）训练一个分类模型：

• 场景1：batch_size=1（逐样本更新）

  • 每次用单个样本计算梯度。
  • 梯度方向完全由该样本决定，不同样本的梯度可能南辕北辙 → 方差极高。
  • 更新路径震荡严重，收敛慢（但可能绕过局部极小值）。

• 场景2：batch_size=128（小批量更新）

  • 用128个样本的梯度平均值更新参数。
  • 噪声被部分平滑 → 方差适中，平衡了稳定性和收敛速度。

• 场景3：batch_size=全部训练数据（批量梯度下降）

  • 梯度是全体数据的平均，方向最准确 → 方差极低。
  • 更新路径平缓，但计算成本高，且可能陷入局部极小值。

---

5. 如何控制梯度方差？

(1) 调整批次大小

• 增大 batch_size 可降低方差，但需权衡内存和计算效率。
• 实践中常用中等批量（如32-256）。

(2) 优化器设计

• 动量（Momentum）：
  通过累积历史梯度方向，降低当前梯度的随机波动影响。

  # PyTorch 中的带动量的SGD
  optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
  

• 自适应学习率方法（如Adam）：
  根据梯度方差自动调整学习率，缓解高方差问题。

(3) 梯度裁剪（Gradient Clipping）

• 限制梯度最大值，防止高方差导致的梯度爆炸。

  torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
  

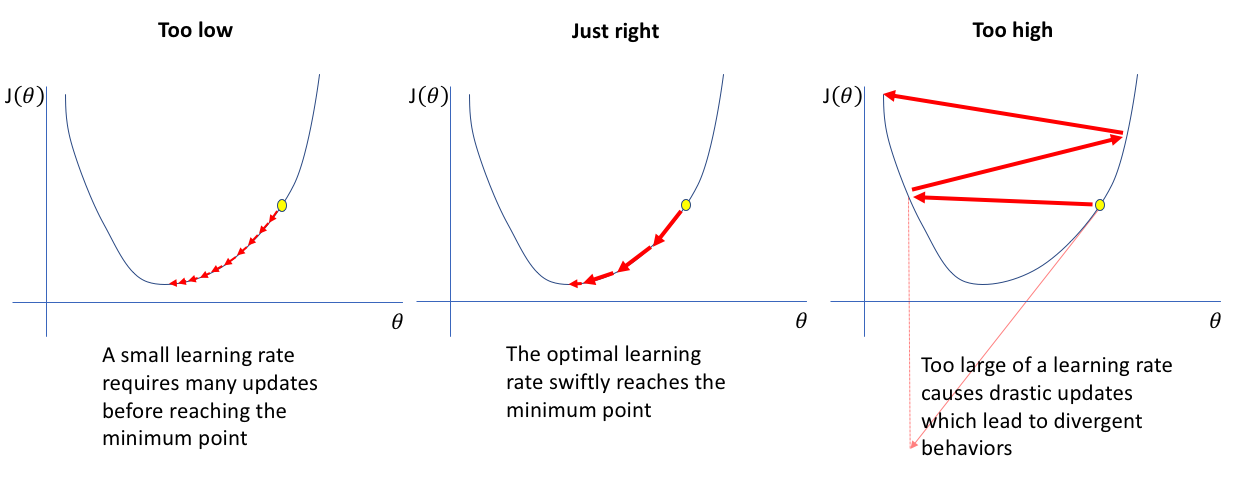
(4) 学习率调整

• 高方差时使用更小的学习率，低方差时增大学习率（见下图）。
  

---

6. 总结

• 梯度方差反映了不同批次数据计算出的梯度的波动程度。
• 高方差导致训练不稳定，但可能提升泛化能力；低方差使训练更平滑，但可能降低模型灵活性。
• 通过调整 batch_size、使用优化器技巧（如动量）和正则化方法，可以平衡方差的影响。
• 实际应用中需根据硬件条件（内存）、数据规模和模型复杂度选择合适的策略。