代数与计算 总结
Lecture 1
课程介绍:
(1) 图同构的群论算法。
(2) 匹配的代数算法。
有三个着重关注的问题:
(1) 三度图的图同构问题 lec2~4。原论文下载。
(2) 可并行的 (i.e. \(\text{quasi-NC}\)) 二分图完美匹配构造一组解的问题 lec5~7。原论文地址。
(3) 同构问题相关的交互式证明协议。
前置知识:线性代数、群论。
|
定义 一张图 \(G = (V, E)\),\(V\):点集,\(E \subseteq \binom V2\):边集。其中 \(\binom V2\) 表示从 \(V\) 中选出两者构成的集族。\(|V|\) 称作 \(G\) 的 order,\(|E|\) 称作 \(G\) 的 size。 定义 生成子图 \(G' = (V, E'), E' \subseteq E\);导出子图 \(G' = (U, E'), U \subseteq V, E' = \{\{i, j\} \mid i, j \in U, \{i, j\} \in E\}\)。\(G\) 是二分图如果 \(\exists V = L \uplus R\),使得 \(\forall e \in E, e = \{l, r\}, l \in L, r \in R\)。其中 \(\uplus\) 表示不交并。\(G\) 不连通如果 \(\exists V = L \uplus R, \forall e \in E, e \subseteq L\) or \(e \subseteq R\)。 |
|
定义 \(M \subseteq E\) 是一个匹配,如果 \(\forall v \in V\),\(\exists\) 至多一个 \(e \in M\),使得 \(v \in e\)。\(M\) 是一个完美匹配,如果把至多改为恰好。 定义 \(G = (L \uplus R, E)\),对 \(S \subseteq L\), 定义 \(N(S) = \{v \in R \mid \exists u \in S, \{u, v\} \in E\}\)。如果 \(|S| > |N(S)|\),称 \(S\) 是 \(L\) 的一个 shrunk subset。
定义 \(G = (V, E)\),对 \(S \subseteq L\),令 \(o(S)\) 为删掉 \(S\) 与其相邻边后的图 \(G[V\setminus S]\) 的奇数大小连通块的个数。如果 \(|o(S)| > |S|\),称 \(S\) 是 \(V\) 的一个 obstruction。
|
上面两个定理说明了完美匹配问题 \(\texttt{PM} \in \text{NP} \cap \text{co-NP}\),也即,判断一个图是否拥有完美匹配和是否没有完美匹配都是 \(\text{NP}\) 的。当然,我们知道,\(\texttt{PM} \in \text P\)。比如在二分图上的增广路(或称匈牙利)算法,一般图上的带花树算法。
下面介绍一种代数做法。这种做法在过程上更简洁,且可并行化。
|
定义 \(A = (a_{ij}) \in M(n, \mathbb F)\),即 \(A\) 是一个在 \(\mathbb F\) 上的 \(n\) 阶方阵。其行列式为 \[\det(A) = \sum\limits_{\sigma \in S_n} \text{sgn}(\sigma)\prod_{i=1}^n a_{i, \sigma(i)}
\]
|
其中 \(x_{ij}\) 为互相独立的不定元。也就是说,\(\det(X_G)\) 是一个(不超过) \(|E|\) 元 \(|V|\) 次多项式,\(\in \mathbb Q[x_{ij}]\)。这样的 \(X_G\) 称作 symbolic matrix。
证明按照行列式的定义是显然的,因为每一项和一个匹配一一对应。但是这相当于把所有问题甩给了如何测试 \(\det(X_G) \neq 0\)。其结果会有指数多项。
我们可以很快想到一个随机做法。关键点在于一个 \(d\) 阶多项式 \(f\) 的零点只有至多 \(d\) 个。
|
引理 (Schwartz-Zippel) \(f\in \mathbb F[y_1, y_2, \ldots, y_m]\) 是一个 \(d\) 阶多项式,那么 \(\text{Pr}_{a_1, a_2, \ldots, a_m \in [2d]^m}(f(a_1, a_2, \ldots, a_m) = 0) \leq \frac 12\)。其中 \(\mathbb F[y_1, y_2, \ldots, y_m]\) 表示在数域 \(\mathbb F\) 上的 \(m\) 元多项式,\([2d]\) 表示 \(\{1, 2, \ldots, 2d\}\)。 |
而行列式是可以高效并行计算的(高斯消元无法做到这一点)。详见 Lecture 5。
更一般地,我们关心如下问题 (Symbolic Determinant Identity Testing, \(\mathtt{SDIT}\))
|
问题 Input 不定元 \(x_1, \ldots, x_m\) 和一个矩阵 \(X\),使得 \(X_{ij} = x_k\) or \(a \in \mathbb Q\)。 Output 是否有 \(\det(X) = 0\)? |
我们有以下结果:(a) \(\mathtt{SDIT}\) 有高效的多项式时间随机做法(Schwartz-Zippel)。(b) \(\mathtt{SDIT}\) \(\in \text P\) 则 algebraic version of \(\text P \neq \text {NP}\)。
\(\mathtt{SDIT}\) 的更多讨论详见 Lecture 7。
|
定义 称 \(G = (V, E)\) 和 \(H = (W, F)\) 同构,如果存在一个双射 \(f:V \in W\) 使得 \(\{v, v'\} \in E\) 当且仅当 \(\{f(v), f(v')\} \in F\)。图同构问题 (\(\mathtt{GI}\)) 即判断两张图是否同构。 |
|
定理 \(\mathtt{GI} \in \text{NP} \cap \text{co-AM}\)。 |
证明详见 Lecture 8。
|
定理 (Babai, 2015) \(\mathtt{GI}\) 可在 \(\exp(O(\log^3 n))\) 解决。 |
在之前,\(\mathtt{GI}\) 最好的算法是 \(2^{\sqrt n} = \exp(\tilde O(n))\),其中 \(\tilde O(n)\) 表示 \(\{n\log^c n\}\)。这一步的跨越是巨大的。
有两种切入 \(\mathtt{GI}\) 的方式:组合 (combinatorial) 和群论 (group-theoretic)。组合做法着重考虑图的性质而群论做法着重考虑同构映射的性质。
组合的一个想法是,考虑从一对对应点开始染色,其他点暂时无色。之后每次把一个点变成它周围点的 multiset,然后为每一种不同的 multiset 分配一个颜色作为下一轮的颜色。这样做上若干轮后,到所有颜色的类都固定了,我们也就找到了一个同构,或在操作中途发现其不同构。这个过程叫做 Weisfeiler-Leman 过程。
|
定理 (Cai-Fürer-Immerman) 存在一对不同构的图,无法在 \(k\) 轮内被区分,而 \(k = O(n)\)。甚至可以是一对三度图,即所有点度数均为 \(3\) 的图。 |
所以这个组合方法是行不通的。
接下来我们介绍三度图上的群论做法。
|
定理 (Luks) 对两个三度图 \(G, H\),存在多项式时间的同构测试算法。 |
Lecture 2
首先我们来看看群论是如何应用到 \(\texttt{GI}\) 上的。
|
定义 \(G = (V, E)\),其自同构集合 \(\text{Aut}(G) = \{f:V \to V \mid {v, v'} \in E \Leftrightarrow \{f(v), f(v')\} \in E\}\)。 |
很显然地,\(\text{Aut}(G)\) 是一个群。\(\text{Iso}(G, H)\) 不是群,是 \(\text{Aut}(G)\) 的一个陪集。
接下来的一个问题是,对 \(n\) 个点的图,其对称群的一个子群 \(S \leq \text{Sym}(V)\) 的大小是指数级的,该如何存储它?
|
定理 对 \(T \subseteq P\),\(\exists T\) 使得 \(\langle T \rangle = P, |T| \leq \lceil \log_2 |P|\rceil\)。 |
证明是显然的,考虑 \(T_0 = \{1\}\),每次随便加入一个在 \(P\) 而不在 \(\langle T_i \rangle\) 里的元素,得到 \(T_{i+1}\),根据 Lagrange 定理可知 \([\langle T_{i+1}\rangle, \langle T_i \rangle] \geq 2\),因此至多只需要 \(\log_2 |P|\) 次包含整个 \(P\)。
因此,今后提到的所有的关于某个对称群的子群的问题,我们全部可以用其生成元集合进行存储、运算。
接下来我们将图同构问题归约到图自同构问题。后者有更好的代数性质。
考虑如果 \(G, H\) 都是连通的,那么构造一个大图把两者的点边全部包含,找到这个大图的自同构群,然后仅把那些交换了 \(G, H\) 位置的生成元留住。如果不连通,根据同构关系的传递性,对 \(G\) 的每一个连通块枚举 \(H\) 的连通块,如果找到同构的连通块,就把两者划掉,继续剩下的部分。
于是我们的任务便是图自同构问题。这个问题可以基于置换群算法的一个框架。
|
给定一个 \(P \leq \text{Sym}(U)\) 的生成集合,有如下问题 问题
|
Membership 是可以归约到 Order 的。因为可以通过把 \(\sigma\) 放到生成集合里看 order 有没有变大。
其中,Membership, Order, Point Stabilizer 是简单的,详见 Lecture 4。Set Stabilizer 是难的,Luks 说明了当 \(|P|=p^k\),其中 \(p\) 是质数时,是简单的。
|
命题 图自同构问题可以归约到 Set Stabilizer 上。
|
|
命题 三度图的同构问题可以归约到三度图的自同构问题。
|
|
命题 (Tutte) \(|\text{Aut}(G)_f| = 2^l\)。
|
在 Lecture 3 中我们会说明为什么在这样的群下 Set stabilizer 是好做的。
接下来,我们考虑如何计算出 \(\text{Aut}(G)_f\)。
上述的群同态是一个限制 (restrict),因此 \(\text{Im}(\pi_i)\text{Ker}(\pi_i) = \text{Aut}(G_{i+1})_f\)。其中 \(GH = \{gh \mid g \in G, h \in H\}\)。换句话说,两部分独立(在一般的商群中,这一点并不成立)。如果我们能够求出 \(\text{Im}(\pi_i), \text{Ker}(\pi_i)\) 的一组生成元,那么 \(\text{Aut}\) 的生成元可以通过 \(\bigcup_{g \in G} gH\) 得到。有关两个陪集的并的计算问题详见 Lecture 3。
我们已经充分讨论了 \(\text{Ker}(\pi_i)\) 的结构,可知其是(在同构的意义上)若干个 \(\mathbb Z_2\) 的直积。
接下来考虑 \(\text{Im}(\pi_i)\)。并不是所有 \(\text{Aut}(G_i)_f\) 的元素都可以扩展到一些 \(\text{Aut}(G_{i+1})_f\) 中的元素。这是因为我们并没有考虑 \(E(G_{i+1}) \setminus E(G_i)\) 所造成的额外限制。考虑令 \(A = V(G_i) \cup \binom {V(G_i)}2 \cup \binom {V(G_i)}3\),即 \(G_i\) 的一二三元集合,
令
其中 \(\exists !\) 表示存在唯一。
那么 \(\sigma \in \text{Aut}(G_i)_f\) 应该稳定化 \(A_1, A_2, A'\)。即 \(\sigma(A_1) = A_1, \sigma(A_2) = A_2, \sigma(A') = A'\)。
也就是说,当我们考虑 \(\text{Im}(\pi_i)\) 的时候,\(V(G_{i+1}) \setminus V(G_i)\) 变成了无标号的。我们需要考虑的只有边的个数关系。
所以,我们的问题变为了,给定一个群 \(P \leq \text{Sym}(A)\),\(A\) 中每个点有一个颜色。我们需要计算 \(P' \leq P\),使得 \(P'\) 稳定化每种颜色。
由于 \(A'\) 和 \(A_1, A_2\) 是两种不同的对 \(A\) 的划分方式,我们得到了 \(A\) 的如下划分

(实际上绿色是空集)
|
定义 有色集合自同构问题 (colored set automorphism)
|
在这里,我们还有特殊性质:\(P\) 是一个 2-group。
Exercises for Lectures 1 and 2
|
Exercise 1. 令 \(H \leq G\),\(|G| = n, |H| = m, l = \frac nm\)。我们称 \(R = \{g_1, g_2, \ldots, g_l\} \subseteq G\) 是左陪集代表元集合,如果 \(g_iH, i \in [l]\) 访问了所有的 \(H\) 的左陪集。右陪集同理。证明存在一个集合 \(R \subseteq G\) 既是左陪集代表元集合,又是右陪集代表元集合。 Solution
|
|
Exercise 2. 如果 \(\sigma\) 有长度为 \(l_1, l_2, \ldots, l_k\) 的环,用 \(n\) 和 \(k\) 表示 \(\operatorname{sgn}(\sigma)\)。 Solution
|
|
Exercise 3. 证明一般图图同构测试可以归约到二分图图同构测试。 Solution
|
|
Exercise 4. 证明图同构问题可以归约到 colored set automorphism 问题,此时输入没有 2-group 的限制。 Solution
|
|
Exercise 5. 我们考虑测试 \(G = (V, E)\) 与 \(H = (W, F)\) 的同构性,\(G\) 是随机图,\(H\) 是任意的,\(|V| = |W| = n\)。也即,\(G\) 中每条边都有 \(\frac 12\) 的概率存在。我们接下来试图设计一个算法 \(A\),使得对至少 \(1 - \frac 1n\) 比例的 \(G\),\(A\) 能对任意的 \(H\) 测试 \(G\) 和 \(H\) 的同构性。
Solution
|
Lecture 3
我们再来重新描述一遍现在的问题。
|
问题 Input \(P \leq \text{Sym}(A)\) 是一个 2-group,\(A = A_1 \uplus A_2 \uplus \ldots \uplus A_c\)。 Output \(Q = \{\sigma \in P \mid \sigma(A_i) = A_i\}\)。 \(P, Q\) 都以生成集合的方式存在。 |
我们知道,\(p\)-group 的一个重要性质就是 Sylow's theorem。
|
定理 (Sylow) 若 \(|G| = p^l \cdot s\),\(p \not| s\),则 \(G\) 存在阶数为 \(p^i\)(\(1 \leq i \leq l\))的子群。 |
这说明 \(G\) 有着平缓的格结构。我们尝试用递归来解决问题。
一个观察是,如果 \(P\) 不 transitive,我们可以对每个轨道单独解决。
|
定义 \(P \leq \text{Sym}(A), B \subseteq A\),称 \(B\) 在 \(P\) 是稳定的,如果 \(\forall \sigma \in P, b \in B\) 都有 \(\sigma(b) \in B\)。\(B\) 是一个轨道,如果 \(B\) 是极小的稳定集合。\(P\) 是 transitive 的,当且仅当其没有非平凡稳定集合。
|
但实际上我们只需要的是
- 对内稳定
- 对外构成划分
这样我们就可以将问题分为两部分,其中第一部分可以递归处理。所以我们的递归条件可以比轨道更松。
|
定义 \(P \leq \text{Sym}(A)\) 是 transitive 的,\(B \subseteq A\),\(B\) 是其一个块 (block),当且仅当 \(B \neq A, B \neq \emptyset\),且 \(\forall \sigma \in P, \sigma(B) = B \text{ or } \sigma(B) \cap B = \emptyset\)。\(P\) 是 primitive 的,当且仅当其没有大小 \(>1\) 的 \(P\)-block。
|
于是可以递归解决 \(P'\) 上的问题。
|
定义 一个块系统是 minimal 的,如果其对应的导出作用 \(P'\) 是 primitive 的。 |
由于一个 \(P\) 上的块系统和对应的 \(P'\) 在 \(\{\sigma(B) \mid \sigma \in P\}\) 上的块系统进行复合可以得到一个每个块更大的系统,因此 primitive 说明这里的 "minimal" 表示的是块数最少。而如果是 maximal 就表示块大小最小。
现在我们来简单研究块系统的结构。
|
命题 \(P\) 是一个 transitive 但不 primitive 的群,\(B\) 是其一个块,\(b \in B\),那么有 \(P_b \leq P_B \leq P\),且 \([P:P_B] = |\{\sigma(B) \mid \sigma \in P\}|, [P_B:P_b] = |B|\)。 |
这是轨道-稳定化子定理的简单应用。
|
命题 \(P \leq \text{Sym}(A)\) 且 transitive,\(b \in A\),那么如果 \(\exists K, \text{ s.t. } P_b < K < P\),那么 \(\exists B\) 是一个块,且 \(b \in B \subset A, |\{\sigma(B) \mid \sigma \in P\}| = [P:K], |B| = [K:P_b]\)。
|
同时我们可以知道,\(K \subseteq P_B, |K| = |P_B|\),故 \(K = P_B\)。这也就是说,块结构和包含了至少一个 \(P_b\) 的子群结构是对应的。这就像“保证所有操作的区间交不为空”那种 OI 题一样。
为了进一步加深这里的印象,我们再回顾一下轨道-稳定化子定理。
|
定理 (轨道-稳定化子, orbit-stabilizer) 令 \(G\) 是一个作用在有限集合 \(X\) 上的群,\(\text{Orb}(x)\) 表示 \(x\) 的轨道,\(G_x=\{\sigma(x) = x \mid \sigma \in G\}\),则有 \(|\text{Orb}(x)|=[G:G_x]\)。
|
也就是说,虽然 \(K\) 看起来只是单方面得到了 \(B\),从而 \(K \subseteq P_B\),但同时也立刻包含了所有的 \(P_B\)。因为如果有一些元素 \(g'\) 在 \(P_B\) 而不在 \(K\) 中,那么 \(g' \cdot x = g \cdot x\) 就会生成新的 \(g'g^{-1} \in P_b\),但是由于我们已经选取了全部的 \(P_b\),这是不可能的。所以 \(P_b < K\) 是重要的。
于是我们可以得到
|
引理 \(P \leq \text{Sym}(A), |A| > 1, |P| = p^l\),那么 minimal \(P\)-block system 有 \(p\) 个块。
|
这不仅为我们提供了平缓的递归过程,也让 base case 变得 trivial。
接下来我们形式化这个想法。
|
定义 \(C_B(Q) = \{\forall b \in B, b \sim \sigma(b) \mid \sigma \in Q\}\),表示 \(Q\) 中保持 \(B\) 中颜色的集合。 |
首先,我们要看如何将两个子问题的结果合并。
|
命题 \(C_B(Q \cup Q') = C_B(Q) \cup C_B(Q'), C_{B \cup B'}(Q) = C_B(C_{B'}(Q))\)。 |
证明是显然的。
需要注意的是,我们并没有保证 \(Q\) 是一个群。因为在 block system 这里,每个块被表示为 \(\sigma \cdot B\),所以 \(Q\) 需要支持是一个陪集。
|
引理 若 \(C_B(\sigma P) \neq \emptyset\),则其是 \(C_B(P)\) 的一个陪集。也就是说,\(C_B\) 内的陪集可提出(代表元可能会变)。
|
接下来我们开始描述递归过程。
|
问题 Input \(P \leq \text{Sym}(A)\),一个 \(2\)-group。\(B \subseteq A\),满足在 \(P\) 稳定,\(\sigma \in \text{Sym}(A)\)。 Output \(C_B(\sigma P)\)。 Initial condition \(B = A, \sigma = \text{id}\)。 |
基于轨道的递归
如果 \(P\) 在 \(B\) 上不 transitive,\(B = B_1 \cup B_2\),其中 \(B_1, B_2\) 在 \(P\) 稳定,那么 \(C_B(\sigma P) = C_{B_1}(C_{B_2}(\sigma P))\)。
如何测试 \(P\) 在 \(B\) 是否 transitive?我们可以用一个 \(|B| \log |P|\) 的朴素算法。
基于块的递归
对于 \(2\)-group,其 minimal \(P\)-block system 一定形如 \(B = B_1 \cup B_2\)。那么 \(P\) 就形如 \(H \cup \tau H\),其中 \(H = P_{B_1} = P_{B_2}\),\(\tau\) 满足 \(\tau(B_1) = B_2, \tau(B_2) = B_1\)。
还有一个问题,就是结果的两侧都是 \(C_B(H)\) 的一个陪集,而我们已经知道它们的并是 \(C_B(P)\) 的一个陪集。
因为 \(\alpha, \beta \in C_B(\sigma P)\),所以 \(C_B(\sigma P) = \alpha C_B(P) = \beta C_B(P), \alpha^{-1} \beta \in C_B(P)\)。因此 \(\langle C_B(H), \alpha^{-1} \beta \rangle \subseteq C_B(P)\),所以有
同时显然地,
故两者相同。
那么该如何找到 \(B_1, B_2\) 呢?
|
命题 (Sims) 在 \(P\) 下,最小的包含元素 \(a, b\) 的块是其在图 \(G = (B, E = \{\sigma(a), \sigma(b)\mid \sigma \in P\})\) 中的连通块。 |
证明不难。被放在了 Exercises 中。
那么重复执行这个操作,我们就可以得到一个 minimal block system,而上文已经保证了这样的块系统一定是只有两个块的。
Base case
\(|B| = 1\),其只包含一个 \(b\),\(P(B) = B\)。\(C_B(\sigma P) = \begin{cases}\sigma P && \sigma(b) \sim b \\ \emptyset && \text{otherwise}\end{cases}\)。
复杂度分析
设 \(f(s)\) 表示 \(|B| = s\) 时最多的递归调用次数。
基于轨道的递归,有
基于块的递归,有
base case
经过简单推导,有 \(f(s) \leq s^2\)。
Lecture 4
我们如果回顾上述过程,会发现还有一点没有解决,就是在 \(P = H \cup \tau H\) 时,如何计算出这样的 \(H\)。更一般地,我们想解决这样的问题:
|
问题 Input 给定 \(P = \langle T \rangle \leq \text{Sym}(A), H\) 是 poly-index, poly-recognizable 的。i.e. \([P:H] = \text{poly}(|A|)\),给定 \(\sigma \in \text{Sym}(A)\) 可以在 \(\text{poly}(|A|)\) 测试是否有 \(\sigma \in H\)。 Output \(H\) 的生成元集合。 |
在我们面对的情况中,\([P:H] = 2, H\) 稳定了 \(B_1, B_2\),所以是 poly-index, poly-recognizable 的。
考虑这样一个过程:维护两个集合 \(X, Y\),\(Y\) 表示 \(H\) 的生成元集合,\(X\) 表示 \(H\) 在 \(P\) 的陪集代表元集合。最初 \(X = \{\text{id}\}, Y = \emptyset\)。加入一个 \(\sigma\) 时,对 \(X\) 中的每个元素 \(\tau\),测试 \(\tau^{-1}\sigma\) 是否在 \(H\) 中,若有则将其加入 \(Y\),否则将 \(\sigma\) 加入 \(X\)。
这样 \(X\) 中每个陪集至多只有一个代表元,\(Y\) 中的元素都和 \(1\) 在同一个陪集里。最终 \(X\langle Y \rangle = G\)。
但并不是仅把所有 \(\sigma \in T\) 加入就可以得到完整的 \(X, Y\)。将 \(\sigma_1^{\pm 1} \sigma_2^{\pm 1} \ldots \sigma_m^{\pm 1}\) 加入可能会使得 \(X\) 或 \(Y\) 增大。
|
命题 (Schreier) \(H \leq G = \langle S \rangle\),\(R\) 是 \(H\) 在 \(G\) 的陪集代表元集合。令 \(\overline g\) 表示 \(g\) 所在陪集在 \(R\) 中对应的代表元。则 \[H = \langle (\overline {sr})^{-1}sr \mid s \in S, r \in R\rangle
\] 更进一步地,我们可以不断加入 \(\sigma = sr, s \in X \cup Y, r \in X\),直到 \(X, Y\) 不再改变,这样得到的 \(X = R, \langle Y\rangle = H\)。
|
这样我们便得到了一个能够生成 \(H\) 的集合。但它不是极小的。我们需要对其进行去重。
我们知道,\(X\) 的大小永远是固定的,等于 \([P:H] = \text{poly}(|A|)\)。如果我们能够找到一些 \(H_0 = H \geq H_1 \geq H_2 \geq \ldots \geq H_k = \text{id}\),使得 \([H_i:H_{i+1}] = \text{poly}(|A|)\),那么我们总是可以将其陪集部分提出,从而对整个 \(H\) 进行分解。
这样的 \(H_i\) 显然是存在的。令 \(H_i\) 表示 \(H\) 中固定了 \(\{1, 2, \ldots, i\}\) 的元素,则根据轨道-稳定化子定理有 \([H_i:H_{i+1}] \leq n-i\)。
这样的过程叫做 Sims sifting algorithm。我们再来重新描述一下其要求。
令 \(P=\langle T \rangle \leq S_n\) 是我们要进行 sifting 的群,即对
计算 \(P_i\) 在 \(P_{i-1}\) 中的陪集 \(C_i\)。其中 \(P_i\) 表示 \(P\) 中固定了 \(\{1, 2, \ldots, i\}\) 的元素。
若完成,有
- 每个 \(\tau \in P\) 都可以写为 \(\tau_1 \tau_2 \ldots \tau_{n-1}\),其中 \(\tau_i \in C_i\)。
- 对每个 \(\sigma \in S_n\),我们可以测试是否有 \(\sigma \in P\),通过
- 对每个 \(\tau_1 \in C_1\),测试是否有 \(\tau_1^{-1} \sigma\) 稳定了 \(1\)。如果没有,\(\sigma \notin P\)。
- 如果有,将其送到下一层,测试是否有 \(\tau_2 \in C_2\) 使其稳定了 \(2\),以此类推。
- \(|P|=|C_1||C_2|\ldots |C_{n-1}|\)。
- poly-index, poly-recognizable 问题的解决。因为这个过程能够去重。
- 特别地,Point Stabilizer \(P_a \leq P\) 可被求出。
现在来重新描述一遍算法流程。
最初我们构建一个 \(n \times n\) 的列表
列表的每个位置要么为空,要么是一个元素。第 \(i\) 行的所有元素构成了 \(C_i\)。\((i, j)\) 中的元素保证稳定化 \(\{1, 2, \ldots, i - 1\}\) 且将 \(i\) 送到了 \(j\)。所以 \(B\) 是上三角的。
sifting 过程如下:对于一个元素 \(\sigma\),从 \(i=1\) 到 \(n-1\),执行如下过程
-
在第 \(i\) 行,如果 \(\not \exists \tau, \text{ s.t. } \tau(i) = \sigma(i)\) (i.e. \(B_{i, \tau(i)}\) 为空),则令 \(B_{i, \tau(i)} = \sigma\)。
否则 \(\sigma \leftarrow \tau^{-1} \sigma\)。可知此时新的 \(\sigma\) 稳定了 \(i\),因此稳定了 \(\{1, 2, \ldots, i\}\),故可以送到下一行。
但同样,并不是将 \(P\) 的生成元集合 sift 就结束了,否则 \(B\) 如何能包含 \(\frac 12 n(n-1)\) 个元素?\(B\) 中的元素并不要求生成无关。
|
定理 当
时,\(C_i\) 为 \(P_{i+1}\) 在 \(P_i\) 的陪集。 这是 Schreier's lemma 在多层时的推广。
|
由此我们可以在 \(O(|A|^6)\) 完成 \(B\) 的构建。参考代码。
由此,我们正式地做完了三度图上的图同构问题。
接下来插入一段张量同构的内容。从第五讲开始我们回到匹配问题。
我们知道矩阵的相似:给定 \(A, B \in M(n, \mathbb F)\),问是否存在 \(L, R \in GL(n, \mathbb F)\),使得 \(LAR = B\)。其中 \(M\) 表示矩阵群,\(GL\) 表示满秩矩阵群。
\(3\)-tensors 是把矩阵的二维数组变为了三维。其可以写成一个矩阵列表的形式。
|
定义 令 \(\overline A = (A_1, \ldots, A_l), \overline B = (B_1, \ldots, B_l), A_i, B_j \in M(n \times m, \mathbb F)\),定义
|
经过这三种作用,且 \(L/R/T\) 均可逆的张量与原张量同构。
|
命题 图同构可以在多项式时间内归约到张量同构。 |
|
命题 (Li-Qiao-Wigderson-Wigderson-Zhang) 二分图同构可以在多项式时间内归约到张量同构。
|
接下来我们介绍图同构在密码学中的一个应用:Goldreich-Micali-Wigderson 零知识协议。
目标:Alice 想要验证 Bob 的身份。
Bob 准备了一个随机图 \(G\),一个随机的排列 \(H\),令 \(H = \pi(G)\)。私钥为 \(\pi\),公钥为 \(G, H\)。任何不知道 \(\pi\) 的人无法同时验证 \(G\) 和 \(H\)。我们以此来设计一个协议。步骤如下
- Bob 生成一个随机排列 \(\sigma\)。令 \(K = \sigma(H)\),向 Alice 发送 \(K\)。
- Alice 根据 \(K\) 向 Bob 随机发送一个 \(0\) 或 \(1\)。
- 如果 Bob 收到了 \(0\),令 \(\tau = \sigma\),否则令 \(\tau = \sigma\pi\),向 Alice 发送 \(\tau\)。
- Alice 检查,如果发送了 \(0\),是否有 \(K = \tau(H)\);如果发送了 \(1\),是否有 \(K = \tau(G)\)。
如果图同构问题是难被破解的,一个不知道 \(\pi\) 的人是无法同时给出 \((K, \tau)\) 使得它们既能符合 \(H\) 又符合 \(G\) 的。因此 Alice 有 \(\frac 12\) 的概率拒绝一个假身份的人。
零知识性:Alice 并不需要知道 \(\pi\) 便可以验证 \(\pi\)。
这个协议不是安全的。因为图同构问题容易被破解。解决方法是将其改为张量同构。
|
张量同构近期的进展: (Xiaorui Sun) \(q^{O(n^{1.8})}\) (在 \(\mathbb F_q\) 上)。之前的成果是 \(q^{n^2}\)。 (Li-Qiao) 在平均情况下 \(q^{O(n)}\)。 对于应用密码学,取 \(n=14, q\) 是一个 \(12\)-bit 质数 (Matrix Equivalence Digital Signature, MEDS)。 |
Exercises for Lectures 3 and 4
这个 Exercises 应该是四次中最难的一次了。大概是因为这两讲也就是最难的两讲了。
|
Exercise 1. 回顾 Sims 给出的算法
请证明它。 Solution
|
|
Exercise 2. 令 \(P \leq \mathrm{Sym}(A)\),\(B \subseteq A\),\(|A| = n, |B| = s\),设计一个算法,使其可以在 \(2^{O(s)} \mathrm{poly}(n)\) 计算 \(\mathrm{Stab}_P(B) := \{\sigma(B) = B \mid \sigma \in P\}\)。(提示:动态规划) Solution
|
|
Exercise 3. 我们尝试将三度图扩展到每个点度数 \(\leq 5\) 的图。
Solution
|
Lecture 5
我们回到匹配问题上。
第一讲中已经介绍了一种随机化的可并行的寻找完美匹配的算法。我们先来解释一下何为并行。
|
定义 在 \(\mathbb F\) 上的算术电路 \(C\) 是一个有向无环图 \(G = (V, E)\),满足
\(C\) 的大小为边集的大小,\(C\) 的深度为最长的叶子到终点的简单路径。 高效的并行计算:\(\text{NC}\) (Nick's class), i.e. \(\text{poly}(n)\)-size, \(\text{polylog}(n)\)-depth。 |
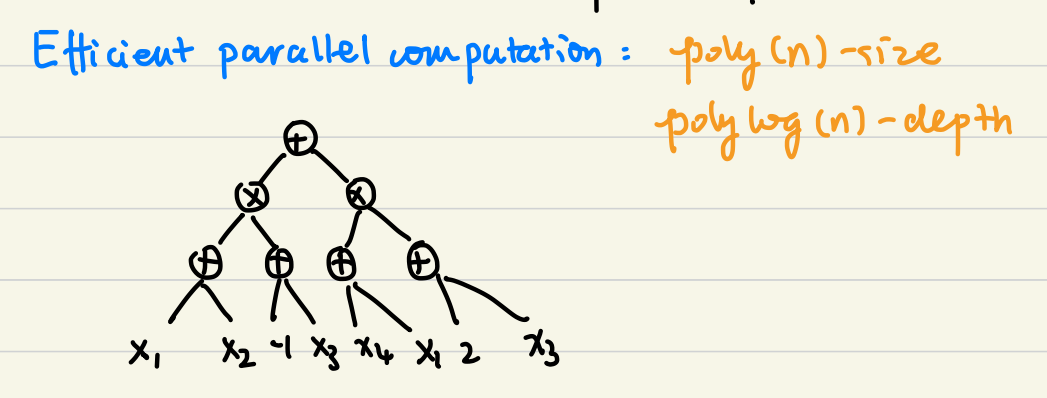
这样,只要有足够多(且 \(\text{poly}(n)\))的计算单元,我们就可以将相同深度的同时计算,这样时间复杂度只和深度有关。
我们知道完美匹配的并行算法基于行列式的并行算法。所以我们现在来看如何并行计算行列式。
把 \((i, \sigma(i))\) 当作一条边,转化为若干个环的形式。
这么做的好处是,我们把贡献分给了每个连通块。接下来我们可以利用行列式的容斥性质,来让每个连通块之间互不影响(不需要是一个排列),由此可以进行 low-depth 的递推。
|
定义 一个 clow 是一条路径 \((i_1, i_2, \ldots, i_l, i_1)\),满足
\(i_1\) 称作这个 clow 的头。 一个 clow 序列 \(\{C_1, \ldots, C_k\}\) 的条件和属性如下
|
|
定理 (Mahajan-Vinay, 1997) \[\det A = \sum_{W:\text{ clow seq}} \text{sgn}(W) \prod_{e \in W} a_e
\]
|
接下来便是考虑用递推算出
设 \(g_{l, u}\) 表示长度为 \(l\),head 为 \(u\) 的所有 clow 的权值和。
其中 \(W_{l, u, v, w}\) 表示从 \(v\) 到 \(w\) 的长度为 \(l\) 的,且走过的所有结点编号比 \(u\) 大的路径权值和。这个数组的含义类似 floyd,可以 \(O(n^4)\) 预处理。
设 \(f_{l, u, v}\) 表示使用了 \(l\) 条边,第一个 clow 的 head 是 \(u\),最后一个的 head \(\leq v\) 的权值和。
\(f_{n, 1, n}\) 便为答案。
这样的复杂度是 \(O(n^4)\) 的。会有 \(O(n^3)\) 的做法吗?

关于对它的深度的验证,在 Exercises 里。
接下来便是本课程第二个较大的问题。我们已经有了一个确定是否存在完美匹配的随机化算法。但是如何构造一组解?
我们给每条边设置一个权重 \(w(e)\)。如果最小权完美匹配是唯一的,那么我们可以通过对权重进行编码来得到一个逐条边确定的算法。
令 \(A_{i, j} = \begin{cases}2^{w(e)} && e \in E \\ 0 && e \notin E\end{cases}\).
则 \(\det A\) 的 lowbit (\(\max k \mid (k \in \mathbb N, 2^k | \det A)\)) 就表示那个最小权完美匹配。
我们每次删掉一条边,得到 \(A'_f\),计算 \(\det A'_f\),如果它的 lowbit 改变了,那就让 \(f \in M\)。这样得到的 \(M\) 就是最小权完美匹配。
所以现在,我们需要为每条边分配一个边权,使得最小权完美匹配唯一。
这里先给出一个随机化算法。Lecture 6, 7 将给出一个确定性算法。
应该能够意识到,如果边权在比较大的范围内随机,那存在两组边权和相同的完美匹配的概率会很小。我们考虑形式化这件事。
|
定义 \(X\) 是一个大小为 \(m\) 的基础集合,\(w: X \to [N]\) 是一个权值函数,\(E \subseteq X, w(E) = \sum_{e \in E} w(e)\),\(\mathcal F \subseteq 2^X\) 是一个集族,成 \(w\) 对 \(\mathcal F\) 是 isolating 的,如果 \(\min_{E \in \mathcal F} w(E)\) 在唯一 \(E\) 上达到。 |
|
引理 (Isolation Lemma, Mulmuley-Vazirani-Vazirani) \(w:X \to [N]\) 均匀独立随机时,\(\operatorname{Pr}[w \text{ isolating for } \mathcal F] \geq 1 - \frac mN\)。
|
那么我们在一个二分图里,令 \(X = E, N = 2|E|\),就可以有 \(\geq \frac 12\) 的概率成功。这样这整个过程就是 \(\text{polylog}(n)\)-depth 的。
Lecture 6
现在我们来介绍一个确定性算法 (Fenner-Gurjar-Thierauf),用来寻找一组 isolating 的 \(w\)。
我们先来研究 isolating 的完美匹配的组合性质。
令 \(M_1, M_2\) 是两组完美匹配。两者的对称差 \(M_1 \triangle M_2\) 是若干个偶环。
|
定义 一个环 \(C\) 在图 \(G\) 中是 nice 的,如果 \(C\) 是两个完美匹配的对称差。 |
|
命题 \(C\) 是 nice 的 \(\Leftrightarrow\) 将 \(C\) 中的点删去的导出子图拥有完美匹配。 |
|
定义 \(G = (L \uplus R, E)\) 是一个拥有完美匹配的二分图,\(C=(v_1, \ldots, v_k)\) 是一个环。\(w:E \to [N]\) 是一个权值函数,\(C\) 在 \(w\) 中的 circulation 为 \[Z_w(C) = |w(v_1, v_2) - w(v_2, v_3) + \ldots + w(v_{k-1}, v_k) - w(v_k, v_1)|
\] |
|
引理 如果所有的 nice 的环拥有非零的 circulation,那么 \(w\) 对所有完美匹配是 isolating 的。
|
我们可以解决一个更强的问题,即找到一组 \(w\) 使得所有的环的 circulation 都不为零,而不仅仅是 nice 的环。因为所有 nice 的环的结构显然更难把握。
突破口在于
|
引理 \(G\) 是一个 \(n\) 个点的图,如果没有 \(\leq r\) 的环,\(r \geq 4\),那么 \(\leq 2r\) 的环的个数至多有 \(n^4\) 个。
|
这个引理,给了我们能够在 \(\text{poly}\) 将问题减小一倍的机会,这样最终的复杂度也会是 \(\text{poly}\)。
我们考虑将每一个环的 circulation 全部乘起来,并使其非零。
构造 \(t\) 组 \(w\),\(w_j(e_i) = 2^{i-1} \bmod j\),令 \(Z_j = \prod_{i=1}^s Z_{w_j}(C_i)\) 表示所有环的 circulation 的乘积。钦定 \(w_0, Z_0\) 是不取模的原始值。需要注意的是由于不存在一个 \(w_0\) 的非空子集和为 \(0\),\(Z_0 \neq 0\)。
可知 \(Z_j \equiv Z_0 \pmod j\)。若 \(\forall 1 \leq j \leq t, Z_j = 0\),那就有 \(\operatorname{lcm}(1, 2, \ldots, t) \mid Z_0\),但 \(Z_0 \leq 2^{n^2 s}\),而当 \(t \geq 7\) 时就有 \(\operatorname{lcm}(1, 2, \ldots, t) > 2^t\),所以让 \(t \geq n^2s\),则一定有一个 \(Z_j \neq 0\)。
对于一般的图来说,\(s\) 可能是指数级的。现在我们用上面的引理来让我们每次处理的 \(s\) 在 \(\text{poly}(n)\)。
令 \(E_1\) 表示所有的最小权完美匹配的边集并。
|
引理 \(G_1 = (V, E_1)\) 的每个完美匹配拥有相同的权值。 |
证明详见 Lecture 7。
也即,所有 \(G_1\) 里的匹配都是 \(G\) 里的最小权完美匹配。所以 \(G_1\) 中,每个 nice 的环的 circulation 都是 \(0\)。
我们可以在 \(G_0\) 中为所有长度 \(\leq 4\) 的环构造一组权值 \(w_0\),使得它们的 circulation 均不为 \(0\)。
那么 \(G_1\) 中不存在 \(\leq 4\) 的环,否则与命题矛盾。因此长度 \(\leq 8\) 的环至多只有 \(n^4\) 个,我们为其构造一组权值 \(w_1\),使得它们的 circulation 均不为 \(0\)。
同理可以构造出 \(G_2, w_2, G_3, w_3, \ldots, G_{k-1}, w_{k-1}\),使得
-
\(G_i= (V, E_i)\),\(E_i\) 为 \(G_{i-1}\) 在 \(w_{i-1}\) 下的所有的最小权完美匹配的边集并。
-
\(w_i\):所有在 \(G_i\) 中的长度 \(\leq 2^{i+2}\) 的环的 circulation 均不为 \(0\)。
-
\(k = \lceil \log_2 n \rceil - 1\)。
那么由于 \(G_{k-1}\) 没有长度 \(\leq 2^{\lceil \log_2 n \rceil}\) 的环,所以其没有任何环,因此完美匹配唯一。
现在考虑所有 \(w_i\) 的笛卡尔积 \(w_0 \times w_1 \times w_2 \times \ldots \times w_{k-1}\) 作为一个新的边权 \(w\),加减法是逐位加减,比较是优先级从前向后的字典序比较。
如果有一个最小权完美匹配 \(M^*\),对于其他所有的 \(M\),\(\exists i < k-1, \text{ s.t. } M \in G_i, M \notin G_{i+1}\)。所以 \(w_i(M) > w_i(M^*), \forall j < i, w_j(M) = w_j(M^*)\)。因此 \(w(M) > w(M^*)\)。故有
|
命题 \(w\) 是 isolating 的。 |
我们考虑笛卡尔积的一个充分描述是,找到一个足够大的 \(B\) 作为进制,然后对数字串进行编码。
也即令
而每一个 \(w_i \leq n^2 \cdot s = n^6\)。由于我们需要求许多条边的 \(w\) 的和再做比较,\(B = n^7\) 是一定可以的。
这样,我们就有了 \(O(n^{\log n}) = 2^{O(\log^2 n)}\) 种权值,每种权值有 \(O(\log^2 n)\) 位,使得对每一张二分图,至少有一种权值可以 isolating。
每种权值的构造可以并行。行列式计算也可以并行。
将所有结果收集的深度是 \(O(\log^2 n)\) 的。
所以最终算法的深度是 \(O(\log^2 n)\),大小是 \(2^{O(\log^2 n)}\) 的,i.e. \(\text{quasi-NC}^2\)。
Exercises for Lectures 5 and 6
这次作业极其简单。
|
Exercise 1. 对 \((23), (124), (1243)\) 依次做 sifting。 Solution
|
|
Exercise 2. 令 \(G = (V, E)\) 为一个完全有向图,\(|V| = n\),边权为 \(a_{i, j}\)。定义 \(D[l, u]\) 为所有长度为 \(l\),head 为 \(u\) 的 clow 的权值和,写出一个 \(D[l, u]\) 的递归式,使其算术电路是 \(\text{poly}(n)\)-size, \(\text{polylog}(n)\)-depth 的。 Solution
|
|
Exercise 3. 证明 \(C\) 是 nice 的 \(\Leftrightarrow\) 将 \(C\) 中的点删去的导出子图拥有完美匹配。证明两个完美匹配的对称差是许多 nice 的环的不交并。 Solution
|
|
Exercise 4. 设计一个算法使其能够计算一个二分图拥有奇数还是偶数个完美匹配。 Solution
|
|
Exercise 5. 设计一个 \(\text{poly}(n)\)-size 的算术电路。使其能够对 \(k \in [n]\) 计算 \(\mathbb Q\) 上的 \(s_k\)。其中 \[s_k(x_1, x_2, \ldots, x_n) := \sum_{S \subseteq [n], |S| = k} \prod_{i \in S} x_i
\] Solution
|
Lecture 7
我们现在来证明
|
引理 令 \(E_1\) 表示二分图 \(G = (V, E)\) 在权值函数 \(w\) 下所有的最小权完美匹配的边集并,\(G_1 = (V, E_1)\) 的每个完美匹配拥有相同的权值。 |
它的一个充分描述是
|
引理 令 \(E_1\) 表示二分图 \(G = (V, E)\) 在权值函数 \(w\) 下所有的最小权完美匹配的边集并,\(G_1 = (V, E_1)\) 不包含 circulation 不为零的环 \(C\)。 |
一件有趣的事是,Lecture 6 的算法过程并没有用到二分图的任何性质。它只用于保证这个引理的正确性。
我们引入匹配多面体 (matching polytopes) 的概念。
|
定义 对于一个 \(G\) 的完美匹配 \(M\),定义其关联向量 \({\bm x}^M \in \mathbb R^m\) 为 \[x_e^M = \begin{cases}1 && e \in M \\ 0 && \text{otherwise}\end{cases}
\] |
|
定义 完美匹配多面体是所有完美匹配在 \(\mathbb R^m\) 中的关联向量的凸包 \[\mathrm{PM}(G) = \operatorname{conv} \{\bm x^M \mid M \text{ is a perfect matching in } G\}
\] |
其中凸包的代数定义
|
定义 对集合 \(S = \{u_1, \ldots, u_k\} \subseteq \mathbb R^m\),其凸包 \(\operatorname{conv}(S) = \left\{\sum_{i=1}^k \alpha_i u_i \mid \alpha_i \geq 0, \sum_{i=1}^k \alpha_i = 1\right\}\) |
权值函数可以很自然地推广到这里。
|
定义 对任意 \(\bm x \in \mathbb R^m\),定义 \[w(\bm x) = \sum_{e \in E} w(e)x_e
\] |
那么就有 \(w(M) = w(\bm x^M)\)。同时根据凸多面体的基本性质,也有
因为 \(w\) 是线性函数,而凸多面体上的线性函数的最值点只可能在顶点。
|
引理 在二分图上,\(\bm x \in \mathrm{PM}(G)\) 当且仅当 \[\begin{aligned}\sum_{e \in \delta(v)} x_e &= 1 && v \in V \\ x_e &\geq 0 && e \in E\end{aligned}
\] 其中 \(\delta(v)\) 表示 \(v\) 的相邻边。 |
也就是说,在这个问题中,整数规划问题和其所对应的线性松弛问题是等价的。我们回顾整数规划的一个定理
|
定理 设线性规划问题所对应的多面体为 \(P=\{A\bm x \leq \bm b \mid \bm x \in \mathbb R^n_+\}\),向量 \(\bm b\) 为整数向量,若 \(A\) 为全单模矩阵 (totally unimodular matrix),即 \(A\) 的任意子阵的行列式均为 \(0,1,-1\),则 \(P\) 的顶点都是整数点。
|
震惊!!原来 Cramer 法则真的不是废物!!!
现在我们来验证这里的 \(A\) 是满足的。
|
证明 我们把线性规划的限制式写出来。 \[\begin{aligned}\operatorname{maximize}\ &\bm c^T\bm x \\ \text{ s.t. } &A\bm x \leq \bm b \\ &\bm x \geq 0\end{aligned}
\] 其中 \(\bm x \in \mathbb R^m\),\(\bm c = (\overbrace{1, 1, \ldots, 1}^{m \text{ times}})^T\),\(A\) 为关联矩阵,第 \(i\) 列只有第 \(i\) 条边对应的两个顶点为 \(1\),\(\bm b= (\overbrace{1, 1, \ldots, 1}^{n \text{ times}})^T\)。 当然,我们这里 \(\operatorname{maximize}\) 什么东西不重要。 完美匹配的限制式则为 \[\begin{aligned}\operatorname{maximize}\ &\ldots \\ \text{ s.t. } &A\bm x = \bm b \\ &\bm x \geq 0\end{aligned}
\] 经典地,我们可以把 \(=\) 改写成 \(\leq\) 并且 \(\geq\),\(a \geq b\) 改写成 \(-a \leq -b\)。同时把 \(x \geq 0\) 也写进去,这样得到了一个新的 \(A'\)。 \[\begin{aligned}\operatorname{maximize}\ &\ldots \\ \text{ s.t. } &A'\bm x \leq \bm b\end{aligned}
\] 考虑 \(A'\) 的一个子方阵,它的每一列只有至多两个 \(1\)。如果有 \(0\) 个,\(\det\) 为 \(0\);如果有 \(1\) 个,可以归纳到更小的子方阵;如果所有列都有 \(2\) 个,由于一行表示的是一个点的全部信息,将行分为那些左侧点所在的行和右侧点所在的行,由于每一列都是在前者有一个 \(1\),后者有一个 \(1\),所以左侧点和右侧点的行和应该相同,\(\det\) 为 \(0\)。因此 \(A'\) 是全单模矩阵。命题得证。 |
我们回到原命题。现在,假如有一个 circulation 不为零的 \(C\),考虑推出矛盾。下面的证明与拉格朗日乘子法的 trick 类似,也即,不为零的线性函数正负两个方向必有一边可以走到更小的,因此不会是极值点。
|
证明 我们试图找到一个多面体的一个点,使得它在所有环 \(C\) 的关联向量的方向上都是内点。这样如果 \(C\) 的 circulation 不为零,正负两个方向必有一边可以让权值变得更小,而只要这个多面体出现了某个权值,由于权值是线性函数,必有一个顶点的权值不大于它,这导致了矛盾。 令 \[\bm x = \frac{\bm x_1 + \bm x_2 + \ldots + \bm x_t}{t}
\] 其中 \(\{\bm x_i\}\) 为所有的最小权完美匹配,也即所有的顶点。我们证明这样的 \(\bm x\) 是内点,证明方法是上述的引理。 由于 \(\{\bm x_i\}\) 是所有的最小权完美匹配,而 \(G_1\) 的边是它们的并,所以 \(\forall e, x_e \geq \frac 1t\)。考虑对任意环 \(C = \{e_1, e_2, \ldots, e_p\}\),令 \[y_e = \begin{cases} x_e + (-1)^i \varepsilon & e = e_i \\ x_e & \text{otherwise} \end{cases}
\] 其中 \(0 < |\varepsilon| \leq \frac 1t\),这样, \[\begin{aligned}\sum_{e \in \delta(v)} y_e &= 1 & v \in V\\ y_e \geq \frac 1t - |\varepsilon| &\geq 0 & e \in E\end{aligned}
\] 所以 \(\bm y \in \mathrm{PM}(G)\)。那么, \[w(\bm x) - w(\bm y) = w(\bm x - \bm y) = \pm \varepsilon Z_w(C)
\] 其中的正负号取决于 \(e_1\) 的选取。我们令 \(\varepsilon\) 的符号与其一致。这样如果 \(C\) 的 circulation 不为零,就有 \(w(\bm y) < w(\bm x)\)。这导致了矛盾。 |
所以,二分图保证了两件事。
- \(A\) 为全单模矩阵。
- \(\bm y\) 的构造。
作业里有两道举一般图上的反例的题。
值得注意的是,我们给定的边权集合 \(\mathcal W\) (\(|\mathcal W| = \mathrm{poly}(n)\)) 是不依赖于 \(G\) 的形态的。我们的命题是对任意 \(G\),在 \(\mathcal W\) 中存在一个权值函数 \(w\)。
我们可以把 Fenner-Gurjar-Thierauf 视作一个特殊情况的 \(\mathtt{SDIT}\) 的解的构造的确定性算法。
|
假设我们有一个黑盒子,盒子中有 \(m\) 个 \(n \times n\) 的矩阵 \(A_1, A_2, \ldots, A_m\),我们的目标是,构造 \(\mathcal W = \{\overline b_1, \overline b_2, \ldots, \overline b_s\} \subseteq \mathbb F^m\),使得 \(s = \mathrm{poly}(n)\) 且 \[\begin{aligned}\forall \{A_1, A_2, \ldots, A_m\}, && &\det\left(\sum_{i=1}^m x_iA_i\right) \neq 0 \\ \Rightarrow \exists 1 \leq j \leq s, && &\det\left(\sum_{i=1}^m \overline b_j(i)A_i\right) \neq 0\end{aligned}
\] 这样的 \(\mathcal W\) 称作 hitting set。 那么我们便可以把上面的算法当作一种特殊情况。
|
太前沿了我们 \(\pmb{\text{quasi-NC}}\) !!!!!!!!!!!!!!!
在一般图上,同样类似地可以定义 \(\mathrm{PM}(G)\),且有
|
定理 (Edmonds) \(\bm x \in \mathrm{PM}(G)\) 当且仅当 \[\begin{aligned}\sum_{e \in \delta(v)} x_e &= 1 && v \in V\\ \sum_{e \in \delta(C)} d_e &\geq 1 && \forall C \subseteq V, |C|> 1, |C| \text{ odd} \\ x_e &\geq 0 && e \in E \end{aligned}
\] 其中 \(\delta(\cdot)\) 表示跨越其内外的边。 |
最后,我们来看算术电路与 symbolic matrix 的关系。
|
定义 一个算术式是除了终点的每个结点的出度都为 \(1\) 的算术电路。 |
或者说,节点构成了一棵树。
给定一个算术式 \(F\),我们想要求出 \(A_1, A_2, \ldots, A_m\),使得 \(\det\left(\sum_{i=1}^m x_iA_i\right)\) 是 \(F\) 所计算的。
我们知道行列式是可以解释为图上的路径计数问题的。所以我们可以使用一个中介:algebraic branching programs, ABP。
|
定义 一个 ABP 是一个带权有向无环图 \(G\),且
\[\sum_{p:\text{ path from } s \to t} \prod_{e \in p} l(e)
\] |
我们可以先把一个算术式转化为一个 ABP,之后把 ABP 转化为 symbolic matrix。做法并不难,如下。
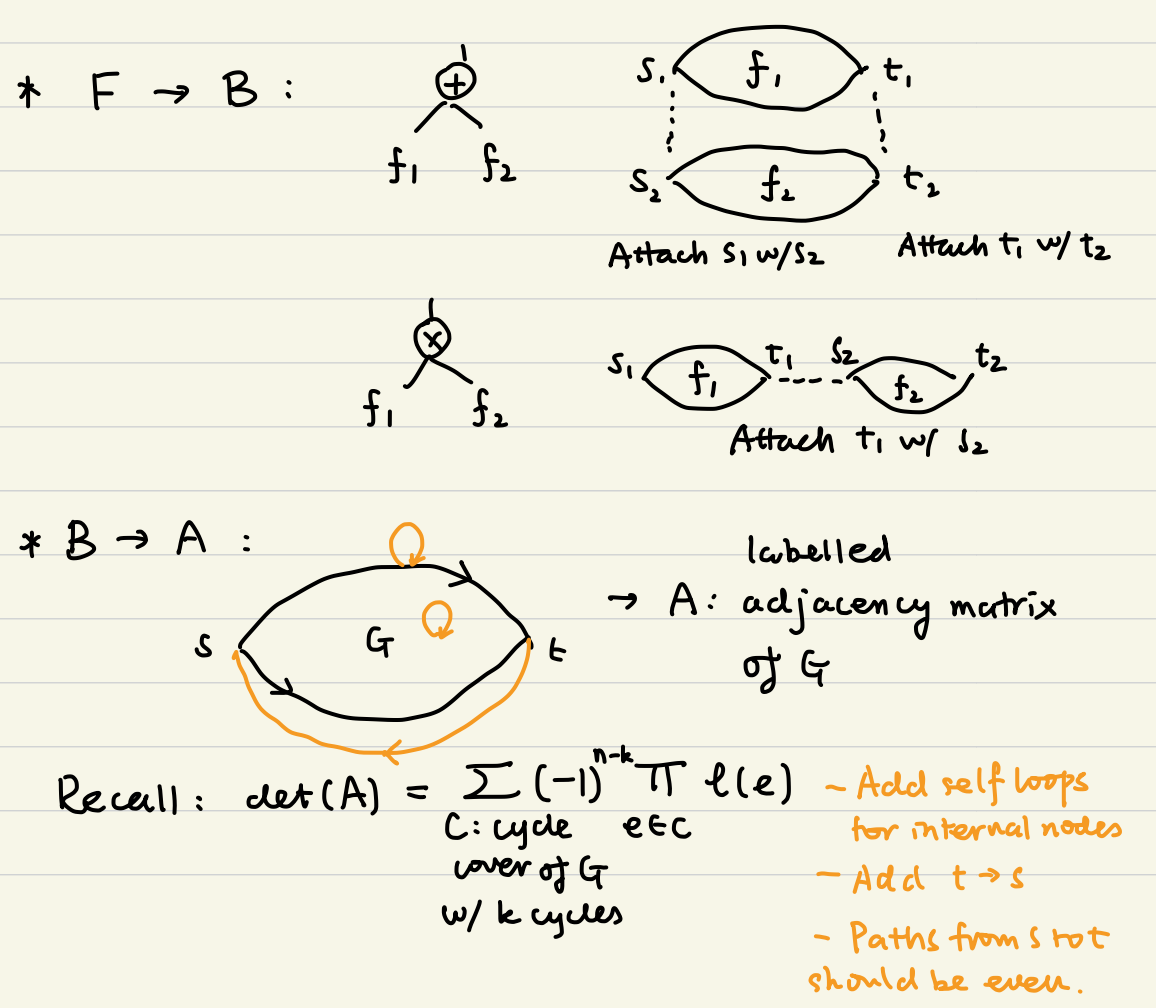
在 \(B \to A\) 的时候,我们加一条 \(t \to s\),并给每个点加上自环。这样 \(s \to t \to s\) 和自环是这张图仅有的环。如果我们能保证每条 \(s \to t\) 的路径都是偶数长度,那么计算行列式时,所有 \(\text{sgn}\) 都是正的,后面计算的便是 \(s \to t\) 的路径条数。
Lecture 8
第八节课补全了之前的进度,讲了一些习题以及讲了一个 \(\mathtt{GNI} \in \text{AM}\) 的协议。我们来讲这个协议。
先预习一下计算理论的相关内容。
复杂度类 \(\text{AM}\) 是一类可在多项式时间内被一个 \(\text{Arthur-Merlin}\) 协议判定的判定性问题。
\(\text{Arthur}\) 是一个拥有标准的图灵机和一个随机数生成设备的验证者,\(\text{Merlin}\) 是一个算力无限的但不可信的证明者,验证者需要验证来自证明者提供的信息,从中提取出合法且自认为有价值的。
最简单的协议是复杂度类 \(\text{MA}\)。此时 \(\text{Merlin}\) 向 \(\text{Arthur}\) 发送一个证明,之后两者不再交互。\(\text{Arthur}\) 使用他的设备来验证其正确性。对误差的刻画类似于 \(\text{BPP}\)。\(\text{MA}\) 与 \(\text{NP}\) 的区别仅在于能否使用随机。
|
定义 一个概率图灵机是一个非确定性图灵机,其基于一个概率分布选择其转移。 形式化地,一个概率图灵机是一个七元组 \(M = (Q, \Sigma, \Gamma, q_0, A, \delta_1, \delta_2)\),其中
每一步,图灵机有 \(\frac 12\) 的概率选择第一套转移,\(\frac 12\) 的概率选择第二套。这个选择不依赖于之前的任何选择。这样,即使是相同的串,其多次放入这个图灵机,有可能有些时候被接受了,有些时候没有被接受。为了适应这个问题,我们称一个语言 \(L\) 是被这个图灵机在误差概率 \(\epsilon\) 下被识别的,如果 \[\begin{cases}w \in L \Rightarrow \operatorname{Pr}[M \text{ accepts }w] \geq 1 - \epsilon \\ w \notin L \Rightarrow \operatorname{Pr}[M \text{ rejects }w] \geq 1 - \epsilon\end{cases}
\] |
概率图灵机与拥有一个随机纸带的确定性图灵机等价。下文将使用后者来描述。
现在我们可以定义
|
定义 复杂度类 \(\text{BPP}\) (Bounded-error Probabilistic Polynomial time) 是一类可在多项式时间内被一个概率图灵机在所有实例误差概率不超过 \(\frac 13\) 下解决的判定性问题。也即,存在确定性图灵机 \(M\) 以及多项式 \(p\),使得
|
其中,\(y\) 是使用的随机纸带,长度是多项式级别的,即 \(p\)。
这里 \(\frac 23, \frac 13\) 可以修改为 \([0, \frac 12)\) 中的任何一个数而不会改变其定义出的集合。这是因为我们可以运行 \(k\) 次,如果 \(\text{accept}\) 次数超过了一半,就认作接受,否则拒绝。这样便是 \(k\) 个 i.i.d. 的随机变量 \(\{X_1, X_2, \ldots, X_k\}, P[X_i = 0] = p, P[X_i = 1] = 1 - p\)。令 \(X = \sum_{i=1}^k X_i, \mu = \mathbb E[X] = (1-p)k\)。
其中 \(0 < \delta \leq \frac 12\),此时 \(e^{-\delta} < (1 - \delta)^{1 - \delta}\),因此 \(c_\delta < 1\)。所以无论任意接近 \(1\) 的 \(p\) 在常数轮内就可以做出任何 \(p > \frac 12\) 的效果。
|
定义 复杂度类 \(\text{MA}\) 是一类可在多项式时间内被一个 \(\text{Arthur-Merlin}\) 协议判定的判定性问题,其中这个协议满足仅进行两轮,且证明者先发送信息。也即,存在一个确定性图灵机以及多项式 \(p, q\),使得对任意输入串 \(x\),\(|x| = n\),
\[\exists z \in \{0, 1\}^{q(n)}, \operatorname{Pr}_{y \in \{0, 1\}^{p(n)}}[M(y, z) \text{ accepts } x] \geq \frac 23
\]
\[\forall z \in \{0, 1\}^{q(n)}, \operatorname{Pr}_{y \in \{0, 1\}^{p(n)}}[M(y, z) \text{ accepts } x] \leq \frac 13
\] |
其中 \(z\) 可以被视为来自 \(\text{Merlin}\) 的证明,证明长度是多项式级别的,即 \(q\)。
|
定义 复杂度类 \(\text{NP}\) 是一类可在多项式时间内被一个确定性图灵机验证的判定性问题。 |
|
定义 复杂度类 \(\text{AM}\) 是一类可在多项式时间内被一个 \(\text{Arthur-Merlin}\) 协议判定的判定性问题,其中这个协议满足仅进行两轮,且验证者先发送其所有随机的结果给证明者,之后证明者发送证明,验证者只能使用这些随机的结果和来自证明者的证明来验证,无法再增加任何随机性。也即,存在一个确定性图灵机以及多项式 \(p, q\),使得对任意输入串 \(x\),\(|x| = n\),
\[\operatorname{Pr}_{y \in \{0, 1\}^{p(n)}}[\exists z \in \{0, 1\}^{q(n)}, M(y, z) \text{ accepts } x] \geq \frac 23
\]
\[\operatorname{Pr}_{y \in \{0, 1\}^{p(n)}}[\forall z \in \{0, 1\}^{q(n)}, M(y, z) \text{ accepts } x] \leq \frac 13
\] |
很显然地,图同构问题 \(\mathtt{GI} \in \text{NP}\)。这是因为证明者发送一个排列 \(p \in \mathrm{Iso}(G, H)\),验证者就可以验证。但图非同构问题 \(\mathtt{GNI}\) 就无法通过类似的方法解决,因为证明两张图不同构是相对困难的。
|
命题 \(\mathtt{GNI} \in \text{AM}\)。 |
有一个经典的协议,验证者从 \(G, H\) 中随机选取一个,并应用一个随机排列,发给证明者。证明者需要指出这是来自 \(G\) 还是 \(H\)。如果他每一次都指对了,说明 \(G \not \cong H\)。这里使用的是 private coins,即没有把所有随机的结果都发给证明者,因为不能让证明者得知选取的是哪一张图。对此,我们有
|
定理 (Goldwasser-Sipser, 1986) 所有使用 private coins 的交互式证明同时有一个 public coins 的交互式证明。 |
所以我们总可以将其改造为符合 \(\text{AM}\) 的一个协议。
接下来是课上介绍的,第二种协议,其原生使用 public coins。
其想法是,考虑
如果 \(G \cong H\),那么 \(|N(G, H)| = n!\),否则等于 \(2\cdot n!\)。我们尝试用这个区别来区分。
令 \(S = \operatorname{encode}(N(G, H)^5)\) 表示将五个 \(N(G, H)\) 的元素进行某种编码(i.e. 某个双射),使其的类型为 \(S \subseteq \{0, 1\}^m, m = \text{poly}(n)\)。
令 \(f:\mathbb F_2^m \to \mathbb F_2^k\) 是一个随机函数。
考虑随机变量 \(X = |\{v \in S \mid f(v) = 0\}|\)。那么就有
|
命题 \[E[X] = \frac{|S|}{2^k}
\] \[\mathrm{Var}[X] = \frac{|S|}{2^k}\left(1 - \frac 1{2^k}\right)
\] \[\operatorname{Var}[X] \leq E[X]
\] |
这样,我们就可以区分一个 \(|S|\) 是小还是大。
令 \(k = \lceil \log(2^2 (n!)^5)\rceil\)
当 \(G \not \cong H\) 时,\(E[X] \geq 4\)。\(G \cong H\) 时,\(E[X] \leq \frac 14\)。
当 \(G \not \cong H\) 时,
当 \(G \cong H\) 时,
因此我们可以设计这样一个协议:
\[\begin{cases}
\sigma_i(K_i) \cong G \text{ or } H \\
\pi_i \in \mathrm{Aut}(K_i) \\
f(K_1, \pi_1, \ldots, K_5, \pi_5) = 0
\end{cases}\]
|
可见,这是一个符合 \(\text{AM}\) 的协议。
Exercises for Lectures 7 and 8
|
Exercise 1. 简要说明如何让算术式转化为 ABP 时每条从 \(s\) 到 \(t\) 的路径均为偶数长度。 Solution
|
|
Exercise 2. 证明在二分图 \(G\) 中每一个完美匹配的关联向量均为 \(\mathrm{PM}(G)\) 的顶点。\(v\) 是一个多面体 \(H\) 的一个顶点,如果存在线性型 \(l\),使得超平面 \(L = \{l(x) = a \mid x \in \mathbb R^m\}\) 满足 \(L \cap H = \{v\}\),且 \(\forall p \in H, l(p) \geq a\)。 Solution
|
|
Exercise 3. 给出一个反例,说明
在一般图上并不成立。 Solution
|
|
Exercise 4. 给出一个反例,说明
\[\begin{aligned}\sum_{e \in \delta(v)} x_e &= 1 && v \in V \\ x_e &\geq 0 && e \in E\end{aligned}
\] 在一般图上并不成立。 Solution
|
|
Exercise 5. 证明
\[\begin{aligned}\sum_{e \in \delta(v)} x_e &= 1 && v \in V\\ \sum_{e \in \delta(C)} d_e &\geq 1 && \forall C \subseteq V, |C|> 1, |C| \text{ odd} \\ x_e &\geq 0 && e \in E \end{aligned}
\] 其中 \(\delta(\cdot)\) 表示跨越其内外的边。 的“仅当”一侧。也即证明在 \(\mathrm{PM}(G)\) 中的 \(\bm x\) 满足这些限制。 Solution
|



 浙公网安备 33010602011771号
浙公网安备 33010602011771号