算法复杂度分析笔记

阶乘渐近复杂度

可以证明

\[n! = o(n^n),\quad n! = w(2^n),\quad \lg(n!) = \Theta(n\lg n). \]

主定理

算法有如下递归式

\[T(n) = a T(n/b) + f(n). \]

其中\(a \ge 1\)且\(b > 1\)为常数. \(n / b\)可以指\(\lfloor n / b \rfloor\)或\(\lceil n / b \rceil\). 则\(T(n)\)有如下渐近界:

  1. 若有某常数\(\varepsilon > 0\)使得\(f(n) = O(n^{\log_ba - \varepsilon})\), 则\(T(n) = \Theta (n^{\log_ba}\)).
  2. 若\(f(n) = \Theta (n^{\log_ba})\), 则\(T(n) = \Theta (n^{\log_ba} \lg n)\).
  3. 若有某常数\(\varepsilon > 0\)使得\(f(n) = \Omega(n^{\log_ba + \varepsilon})\), 且对常数\(c<1\)所有足够大的\(n\)均有\(af(n / b) \le cf(n)\), 则\(T(n) = \Theta (f(n))\).

分治策略

选择算法

对输入规模为\(n\)的数组, 找到其中第\(i\)小的元素.

最坏情况线性时间选择算法SELECT:

  1. 将数组分为\(\lceil n/5 \rceil\)组, 每组5个元素, 最后一个组可能不满.
  2. 依次找到每组中位数元素.
  3. 对各组的中位数, 使用规模为\(\lceil n/5 \rceil\)的SELECT算法找到所有中位数的中位数\(x\).
  4. 利用\(x\)作为主元使用快排的划分算法. 左侧的元素比\(x\)小, 右侧的元素比\(x\)大. 设\(x\)为第\(k\)大的元素.
  5. 根据\(i\)的值, 若\(i = k\), 返回\(x\); 若\(i < k\), 对左侧子数组调用SELECT; 否则对右侧数组调用SELECT.

算法的核心在于选择中位数的中位数\(x\)作为主元, 保证\(x\)不会很大也不会很小, 左右两侧子数组足够的"均衡". 由于\(x\)是各组中位数的中位数, 除了最后一个可能不满的组和包含\(x\)的组, 至少还有一半组中至少3个元素大于\(x\). 可证明所有大于\(x\)的元素个数至少为\(3n/10 - 6\), 同样所有小于\(x\)的元素个数至少为\(3n / 10 - 6\). 这样第5步中不管选择左子数组还是右子数组, 其规模至多为\(7n/10 + 6\).

第1, 2, 4步复杂度为\(O(n)\), 第3步为\(T(\lceil n/5 \rceil)\), 第5步至多为\(T(7n/10 + 6)\). 即

\[T(n) \le T(\lceil n/5 \rceil) + T(7n/10 + 6) + O(n). \]

用代换法可证明\(T(n) = O(n)\).

分支定界法

搜索问题可使用状态空间树表示, 节点有:

  • 活跃节点: 本身已生成, 其子节点均未生成.
  • E节点: 正在生成子节点的活跃节点.

搜索策略:

  • 回溯: DFS, 一个节点可以多次成为E节点.
  • 分支定界法: 节点只成为一次E节点, 生成所有子节点. 每个节点有定界函数, 是以该节点为根的子树解空间优化准则函数的界. 用于选择下一个E节点及剪枝. 扩展节点时优先选择当前界最优的活跃节点.
  • 启发式算法\(A^*\): 节点只成为一次E节点, 生成所有子节点. 每个节点有一个估值函数, 为该节点到最终解距离的估值. 用于选择下一个E节点.

流动推销员问题

距离矩阵\(D = (d_{ij})_{n \times n}\)表示从\(i\)到\(j\)的费用, 对角线全为\(\infty\). 将原始距离矩阵进行Reduction, 每行或每列减去最小值, 使每行每列至少有一个0, 将累计减的值作为节点费用的下界. 分支时, 选择一个零元素决定是否从\(i \rightarrow j\):

  • 左子节点: 选择从\(i \rightarrow j\), 删除\(i\)行和\(j\)列, 并置\(d_{ji} \leftarrow \infty\).
  • 右子节点: 选择\(i \nrightarrow j\), 置\(d_{ij} \leftarrow \infty\).

同顺序加工任务安排

有\(n\)项待加工任务, 工序均为机器\(m_1 \rightarrow m_2 \rightarrow m_3\), 每个机器同一时间只能加工一项任务. 时间矩阵记为\(T = (t_{ij})_{n \times 3}\). 寻找总时间最优的加工顺序.

每个节点加工时间下界\(t^*\)为:

  • 若第一个任务为\(i\), \(t^* = t_{i1} + \sum_{j=1}^n t_{j2} + \min_{j \ne i} \{t_{j3}\}\).
  • 若前两个任务为\(i,j\), \(t^* = t_{i1} + t_{j1} + \sum_{k \ne i} t_{k2} + \min_{k \ne i,j} \{t_{k3}\}\).
  • 若前三个任务为\(i,j,k\), \(t^* = t_{i1} + t_{j1} + t_{k1} + \sum_{l \ne i,j} t_{l2} + \min_{k \ne i,j,k} \{t_{l3}\}\).

贪心算法

区间调度问题

有\(n\)个需求区间\(\{[s(i),f(i)), i = 1, 2, \dots, n\}\), 找出最大的相容需求(区间不重叠)集合.

策略: 选择最早结束的需求. 需求按\(f(i)\)升序排列, 每次找到结束时间最小的需求, 同时拒绝与该需求有矛盾的其他需求.

最小延迟调度问题

有\(n\)个任务, 每个任务需要连续的\(t_i\)时间, 同时有截止时间\(d_i\). 找到一个任务安排, 各任务时间不重叠, 且最大延迟\(L = max_i l_i\)最小, 若任务安排的结束时间\(f(i) > d_i\), \(l_i = f(i) - d_i\), 无延迟则为0.

策略: 所有任务按照截止时间从小到大依次无间隙地安排.

最短路径Dijkstra算法

带权有向图\(G = (V, E)\), 所有权值均非负. 给定源点\(s\), 找到每个点到\(s\)的最短路径. 维护一个优先级队列\(Q\), 存储每个点\(v\)目前到\(s\)的最短距离\(v.d\). 集合\(S\)为已经解决的点.

  1. 初始化\(S = \emptyset\), \(Q\)中只有\(s.d \leftarrow 0\), 其余节点\(v.d \leftarrow \infty\).
  2. 当\(Q\)不为空, 找到\(v.d\)最小的节点\(v\), \(S = S \cup \{v\}\).
  3. 对\(v\)的每个后继节点\(u\), 更新\(u.d = \min \{u.d, v.d + w(v,u)\}\), 同时更新\(u.\pi\)表示\(u\)目前的前趋节点.

复杂度分析: 对优先级队列\(Q\), INSERT和FIND-MIN分别进行了\(|V|\)次, DECREASE-KEY(算法第3步)进行|E|次. 若各操作复杂度均为\(O(\log V)\), 总复杂度为\(O((V+E) \log V)\).

最小生成树算法

无向带权图\(G = (V, E)\)中找到一棵树, 使其边权值之和最小.

Prim算法

输入为图\(G\)和一个根节点\(r\). 算法维护子树\(A\), 初始只含\(r\), 逐渐扩展为最小生成树. 每次扩展时找到\(A\)和\(G - A\)中节点之间的最小边加入\(A\)中. 实现时, 使用优先级队列\(Q\)维护\(G - A\)中每个节点到\(A\)的最小距离. 总复杂度为\(O((V+E) \log V) = O(E \log V)\).

Kruskal算法

初始没有任何边. 按照权重从小到大遍历所有边, 若加入一条边不出现环, 则添加此边; 否则舍弃此边. 直到构成一棵生成树. 添加边时, 使用并查集维护一个森林. 初始每个节点为一个树, 通过\(\text{Find-Set}(u) == \text{Find-Set}(v)\)判断两个节点目前是否在同一个子树中, 通过Union合并两棵子树(添加一条边).

若使用树结构构造并查集, 同时增加按秩合并和路径压缩功能, 算法运行总时间为\(O(E \log E) = O(E \log V)\).

自适应Huffman编码

维护一棵编码树(满二叉树), 根据输入字符动态地调整, 每个节点有唯一编号和权重两个属性. 编码树满足并维护以下兄弟属性:

  1. 父节点编号大于子节点.
  2. 编号大的节点权值一定也大.

同时定义节点所在的块为所有权值相同的节点.

初始空树根节点为NYT, 权重为0. 每次读取新字符时, 将NYT节点变为包含NYT节点和权重为1的该字符节点的子树, 子树的根节点权重为1, 同时需要递归地更新父节点的权重(加一)直到树根, 这种情况输出编码为原NYT节点的路径加新字符. 若读取树中已存在的字符, 将其权重加一, 同时递归地更新父节点权重直到树根, 这种情况输出编码为该字符节点路径. 为维护兄弟属性, 在递归地更新第一个节点权重之前, 要检查其编号是否为块内最大的, 若不是, 先将其与编号最大的节点交换位置再向上更新权值.

最小费用有向树

在有向图中, 指定一个节点为根节点, 有向树为只有根节点入度为0, 其余节点入度为1有弱连通图. 若每边有一个费用, 最小费用有向树为总费用最低的有向树.

策略:

  1. 对除了根节点的每个节点\(v\), 将所有入边费用\(c_e\)均减去最小的费用\(y_v\)得到\(c_e'\), 选择\(c_e'\)为0的那条边(最小费用的入边)加入\(F^*\).
  2. 若这样的\(|V| - 1\)条边\(F^*\)构成了一棵有向树, 返回. 否则对于\(F^*\)中每个环\(C\), 将其收缩为一个超节点. 得到收缩后图\(G'\), 递归地在\(G'\)中找到具有费用\(c_e'\)的最小费用有向树\(F'\). 将每个环\(C\)展开, 将\(F'\)中到\(C\)的入边保留, 同时删除环\(C\)中与该入边同一个后继的边. 这样形成的是图\(G\)的最小费用有向树.

拟阵

一个拟阵为一个序对\(M = (S, l)\). \(S\)为一个非空有限集合, \(l\)为\(S\)的非空子集族, 称为\(S\)的独立子集. 满足:

  1. 遗传性: 若集合\(B \in l\)且\(A \subseteq B\), 则\(A \in l\). \(\emptyset \in l\).
  2. 交换性: 若\(A, B \in l\)且\(|A| < B\), 则存在某个元素\(x \in B - A\)使得\(A \cup \{x\} \in l\).

例如图拟阵\(M_G = (S_G, l_G)\), 对于一个图\(G\), \(S_G\)为其边集, \(l_G\)表示\(G\)所有无回路的边集.

对独立子集\(A \in l\), 若不存在任何一个元素\(x \notin A\), \(A \cup \{x\} \in l\), 则称\(A\)为最大的独立子集. 所有最大独立子集大小均相同.

对一个拟阵, 若\(S\)中每个元素均有一个正的权值, 则存在一个贪心算法找到总权值最大的独立子集\(A\). 策略为:

  1. 初始置\(A \leftarrow \emptyset\). 将\(S\)中所有元素按照权值从大到小排序.
  2. 依次取出\(S\)的元素\(x\), 若\(A \cup \{x\}\)仍是独立的, 则将\(x\)加入\(A\).

最终得到的\(A\)为最优独立子集.

动态规划

带权区间调度

在区间调度问题的基础上, 每个需求区间有一个权值\(v_i\). 需要找出一组相容的需求区间, 使得权值之和最大.

策略: 仍将\(n\)个区间按照结束时间\(f(i)\)升序排列, 记\(p(i)\)为区间\(i\)之前与\(i\)不冲突的最靠后的区间. 记\(O_i\)为前\(i\)个需求构成问题的最优解, 对应最大权值记为\(\text{OPT}(i)\). 在计算\(O_n\)时, 考虑是否保留最后一个区间\(n\). 如果保留, 则后续考虑前\(p(n)\)个区间的最优解; 如果不保留, 后续考虑前\(n-1\)个区间的最优解.

\[\text{OPT}(n) = \max \{\text{OPT}(p(n)) + v_n, \text{OPT}(n-1)\}. \]

且\(n \in O_n\)当且仅当\(\text{OPT}(p(n)) + v_n \ge \text{OPT}(n-1)\). 可以以此回溯最优解.

背包问题

有\(n\)个需求, 每个需求\(i\)有值\(v_i\)和权\(w_i\). 目标是找到一个需求集合, 在总权不超过\(W\)的前提下, 使得总值最大.

策略: 记\(\text{OPT}(i, w)\)为使用前\(i\)个需求在总权不超过\(w\)下的最优总值. 若\(w < w_i\), 不能选择第\(i\)个, \(\text{OPT}(i, w) = \text{OPT}(i-1, w)\), 否则

\[\text{OPT}(i, w) = \max \{\text{OPT}(i-1, w), v_i + \text{OPT}(i-1, w - w_i)\}. \]

最优解选择\(i\)当且仅当\(v_i + \text{OPT}(i-1, w - w_i) \ge \text{OPT}(i-1, w)\).

算法复杂度为\(O(nW)\), 在\(W\)不太大时有意义.

序列对比

给定两个串\(X = x_1x_2 \dots x_m\)和\(Y = y_1y_2 \dots y_n\), 考虑\(X\)和\(Y\)进行比对, 即令\(X\)和\(Y\)中字符进行匹配. 称\(X\)和\(Y\)中没有配对的位置为一个空隙, 有空隙代价\(\delta > 0\). 若\(x_i = p, y_j = q\), 则配对\((i,j)\)有错配代价\(a_{pq}\). 匹配的代价为空隙代价和错配代价之和. 需要找到代价最小的匹配.

策略: 令\(\text{OPT}(i,j)\)为\(X\)的前\(i\)个字符与\(Y\)的前\(j\)个字符匹配的最小代价. 对于\(i \ge 1\)且\(j \ge 1\), \(x_i\)可以与\(y_j\)配对, 或者\(x_i\)和\(y_j\)其中之一变为空隙, 有

\[\text{OPT}(i,j) = \min \{a_{x_iy_j} + \text{OPT}(i-1,j-1), \delta + \text{OPT}(i-1,j), \delta + \text{OPT}(i,j-1)\}. \]

基情况为\(\text{OPT}(i,0) = i \delta\)和\(\text{OPT}(0,j) = j \delta\). 可以通过\(\text{OPT}(i,j)\)进行回溯匹配情况.

朴素算法时间复杂度为\(O(mn)\), 空间复杂度为\(O(mn)\). 序列对比问题等价于对一个\((m+1)(n+1)\)的有向图网格找到\((0,0)\)到\((m,n)\)的最短路径. 其中横向和纵向边权重均为\(\delta\), 斜向边权重为对应的错配代价.

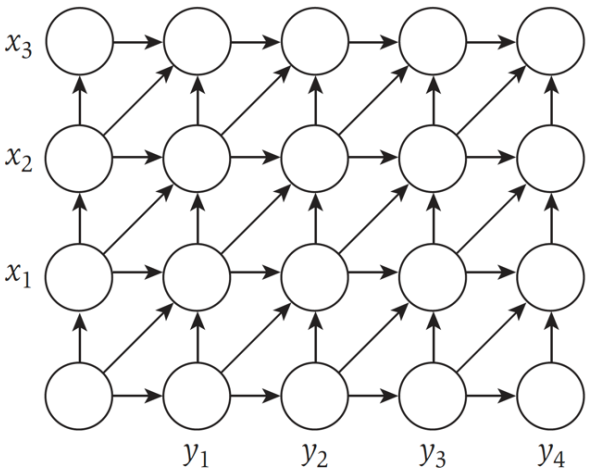
实际可以给出更省空间的算法. 首先迭代时只需要维护两列数组(大小为\(O(m)\))即可找到所有\((0,0)\)到\((i,j)\)的最短距离, 记为\(f(i, j)\). 同理也可以用\(O(m)\)的空间从\((m,n)\)逆向得到所有\((i,j)\)到\((m,n)\)的最短距离, 记为\(g(i,j)\). 对每一列\(0 \le k \le n\), 记\(q\)为使\(f(q,k) + g(q,k)\)最小的行下标, 则最终解的最短路径通过\((q,k)\).

由此给出分治算法, 沿中间列划分网格, 计算每个\(f(i,n/2)\)和\(g(i, n/2)\), 时间复杂度为\(O(m,n)\), 空间为\(O(m)\). 找到令\(f(i,n/2)+g(i,n/2)\)最小的\(i\), 记录\((i,n/2)\)其为最终解路径上一个点. 对左下部分, 递归地找到\((0,0)\)到\((i,n/2)\)的最短路径. 对右上部分, 递归地找到\((i,n/2)\)到\((m,n)\)的最短路径. 记算法复杂度为\(T(m,n)\), 有

\[T(m,n) = O(mn) + T(q, n/2) + T(m-q, n/2). \]

代换法得\(T(m,n) = O(mn)\). 而算法空间仅为\(O(m+n)\).

最短路径算法

设一个带权有向图\(G = (V,E)\), 允许出现负边, 但无负圈. 记\(|V| = n\), \(|E| = m\). 有向边权值矩阵\(W = (w_{ij})_{n \times n}\). 介绍两种动态规划的最短路径算法.

Bellman-Ford算法

给定终点\(t\), 求每个点到\(t\)的最短路径. 对每个点\(v \in V\), 维护数组\(M[v]\). 初始时, 令\(M[t] = 0\), 且其余点\(v\)有\(M[v] = \infty\). 进行如下迭代:

对\(i = 1, 2, \dots, n - 1\):
\(\quad\)以任意次序遍历各节点\(v \in V\):
\(\qquad\)更新\(M[v] = \min \{M[v], \min_{(v,u) \in E} \{w_{vu} + M[u]\}\}\).

最终得到的数组\(M[v]\)即为\(v\)到\(t\)的最短距离.

为恢复最短路径, 为每个节点\(v\)维护一个指针\(\text{First}(v)\), 指向目前\(v\)到\(t\)最短路径上\(v\)的下一个节点. 当\(M[v]\)更新时, \(\text{First}(v)\)也更新为对应的\(u\).

算法的复杂度为\(O(mn)\).

Floyd-Warshall算法

维护矩阵\(D^{(k)} = (d^{(k)}_{ij})_{n \times n}\), \(k = 0, 1, \dots, n\). \(d^{(k)}_{ij}\)表示从\(i\)到\(j\)只经过\(1 \sim k\)的中间节点的最短距离. 初始\(d^{(0)}_{ij} = w_{ij}\). 当\(k \ge 1\), 有迭代式

\[d^{(k)}_{ij} = \min \{d^{(k-1)}_{ij}, d^{(k-1)}_{ik} + d^{(k-1)}_{kj}\}. \]

最终\(i\)到\(j\)的最短距离为\(d^{(n)}_{ij}\). 算法时间复杂度为\(O(n^3)\).

若要恢复最短路径, 可以同时维护另一节点矩阵\((\pi^{(k)}_{ij})_{n \times n}\), \pi^{(k)}_{ij}表示\(d^{(k)}_{ij}\)对应最短路径中\(j\)的前趋节点. 初始若\(i = j\)或\(w_{ij} = \infty\), \(\pi^{(0)}_{ij} = NIT\); 否则\(\pi^{(0)}_{ij} = i\). 迭代式为:

\[\pi^{(k)}_{ij} = \begin{cases} \pi^{(k-1)}_{ij},\,d^{(k-1)}_{ij} \le d^{(k-1)}_{ik} + d^{(k-1)}_{kj}\\ \pi^{(k-1)}_{kj},\,d^{(k-1)}_{ij} > d^{(k-1)}_{ik} + d^{(k-1)}_{kj} \end{cases}. \]

网络流

一个流网络为一个有向图\(G = (V, E)\), 每条边\(e\)有一个非负容量\(C_e\). 所有容量均为整数. 存在单一源点\(s\), 其入度为0; 存在单一汇点\(t\), 其出度为0. 每个节点至少有一条边连接.

一个\(s-t\)流\(f\), 在每条边\(e\)上有流量\(f(e)\)满足\(0 \le f(e) \le C_e\). 除\(s\)和\(t\)外每个节点入流量等于出流量. 该流\(f\)的值记为\(v(f)\)定义为源点流出的总流量.

最大流的Ford-Fulkerson算法

给定一个流网络\(G\), 可以使用Ford-Fulkerson算法寻找最大流.

对流网络\(G\)和一个流\(f\), 定义剩余图\(G_f\), 其节点与\(G\)相同. 对于\(G\)中一条边\(e = (u, v)\), 其有流量\(f(e)\):

  1. 若\(f(e) < C_e\), 该边可以正向推流. 在\(G_f\)中有这条边\((u, v)\), 容量为\(C_e - f(e)\), 称为前向边.
  2. 若\(f(e) > 0\), 该边可以反向撤消流量. 在\(G_f\)中有反向边\((v, u)\), 容量为\(f(e)\), 称为后向边.

将剩余图中一条边的容量称为剩余容量.

若\(G_f\)中存在一条\(s-t\)的简单路径\(P\), 称\(P\)为流\(f\)的一条增广路径, \(P\)上的边最小容量为最小剩余容\(C_P\). 可以利用该路径对流\(f\)进行一次增广: 若\(P\)上某条边\((u, v)\)为前向边, 在\(f\)中将\(f((u, v))\)增加\(C_P\); 若\(P\)上某条边\((u, v)\)为后向边, 在\(f\)中将\(f((v, u))\)减少\(C_P\). 增广后新的流为\(f'\), \(v(f')\)比\(v(f)\)恰好大\(C_P\).

Ford-Fulkerson算法初始\(f\)所有边流量均为0, 不断在剩余图中寻找\(s-t\)的简单路径并对流增广, 同时更新剩余图, 直到剩余图中没有\(s\)到\(t\)的路径.

设\(G\)中边数为\(m\), 算法运行时间为\(O(mC)\), \(C\)为从\(s\)流出的容量和.

称\(G\)的一个\(s-t\)割\(A-B\)是节点的一个划分\((A, B)\), 且\(s \in A, t \in B\). 割的容量\(c(A, B)\)为从A流出的边容量之和. Ford-Fulkerson找到的最大流\(f\)对应\(s-t\)的最小容量割\((A, B)\). 令\(A\)为剩余图\(G_f\)中\(s\)可达的所有节点集合, \(B\)为\(V - A\), \(v(f) = c(A, B)\). 所有\(A\)到\(B\)的边均为最大流量, 所有\(B\)到\(A\)的边均无流量.

设计一个缩放的最大流算法, 选择增广路径时只考虑\(G_f\)中容量大于阈值\(\Delta\)的边, 当在某一\(\Delta\)下找不到增广路径时, 将\(\Delta\)缩小一半, 直到\(\Delta\)变为1时无增广路径则停止. 若\(G\)中边数为\(m\), 缩放最大流算法时间为\(O(m^2 \log C)\).

二分匹配问题

一个二部图\(G = (V, E)\)是一个无向图, 且节点可以划分为\(X\)和\(Y\)两部分, \(E\)中所有边的两个端点均分别在\(X\)和\(Y\)中. 二部图\(G\)的一个匹配是一个边集\(M\), \(G\)的每节点至多在\(M\)的一条边上. 二分匹配需要找到一个规模最大的匹配.

二分匹配可以自然地转为最大流问题. 将所有无向边转化为\(X\)到\(Y\)的有向边, 增加源点\(s\)到\(X\)中所有节点有边, 增加汇点\(t\)被\(Y\)中每个节点指向. 每条边容量为1. 这样得到流网络\(G'\). 利用Ford-Fulkerson算法在\(O(mn)\)时间内找到\(G'\)的一个最大流, 对应\(G\)的一个最大匹配.

若二部图有\(|X| = |Y|\), 则其或者有一个完美匹配, 或者存在子集\(A \subseteq X\), \(A\)的邻居\(|\Gamma(A)| < |A|\). 如果其有一个完美匹配, 则任意子集\(A \subseteq X\), 均有\(|\Gamma(A)| \ge |A|\).

NP完全性

抽象问题\(Q\)是在问题实例集合\(I\)和问题解集合\(S\)上的一个二元关系. 对于判定问题, 解集合为\(\{0,1\}\).

为使问题实例能被算法解决, 要将问题实例编码. 编码是从抽象对象集合到二进制串的映射\(e\). 对抽象判定问题\(Q\)用\(e\)编码, 得到对应的具体判定问题\(e(Q)\). 如果一个抽象问题实例\(i\)的解为\(Q(i) \in \{0,1\}\), 则编码后具体问题实例\(e(i)\)解也为\(Q(i)\). 对于无意义(无抽象问题实例对应)的编码, 规定其解为0.

编码有可能影响算法求解的效率. 对某个抽象问题, 若有两个编码\(e_1\)和\(e_2\)存在两个多项式时间可计算的函数\(f_{12}\)和\(f_{21}\), 使得任何抽象实例\(i\)均有\(f_{12}(e_1(i)) = e_2(i)\)且\(f_{21}(e_2(i)) = e_1(i)\), 称这两个编码是多项式相关的. 对某一抽象问题, 使用任何多项式相关的编码不影响其多项式可解性. 用\(<>\)表示对一个抽象对象的标准编码, 例如对图\(G\)使用\(<G>\)表示图的标准编码.

一个具体判定问题\(Q\)可以看作是一个定义在字母表\(\Sigma = \{0,1\}\)上的语言\(L\), \(L = \{x \in \{0,1\}^* : Q(x) = 1\}\).

一个算法\(A\), 如果对\(x\)输出\(A(x) = 1\), 称\(A\)接受\(x\); 如果输出\(A(x) = 0\), 称\(A\)拒绝\(x\). 被\(A\)接受的语言为所有\(A(x)\)的串组成的集合.

如果对任意\(x \in L\), \(A\)在\(|x|\)多项式的时间接受\(x\), 称语言\(L\)在多项式时间被\(A\)接受.

如果对任意串\(x \in \{0,1\}^*\), \(A\)可以在\(|x|\)多项式时间接受所有\(x \in L\)且拒绝所有\(x \notin L\).

复杂类\(P\)为在多项式时间可解的具体问题集合, 定义为

\[P = \{L \in \{0,1\}^* : \text{存在一个算法}A\text{, 可以在多项式时间判定}L\}. \]

在多项式时间内, 这等价于

\[P = \{L \in \{0,1\}^* : \text{存在一个算法}A\text{, 可以在多项式时间接受}L\}. \]

定义一个验证算法\(A\)以具体问题实例\(x\)和一个证书二进制串\(y\)作为输入. 如果\(A(x,y) = 1\), 称\(A\)验证了\(x\). 由\(A\)验证的语言为\(L = \{x \in \{0,1\}^*: \exists y \in \{0,1\}^*, A(x,y) = 1\}\).

复杂类\(NP\)为在多项式时间可验证的具体问题集合. 语言\(L \in NP\), 当且仅当存在一个验证算法\(A\)和常数\(c\)满足

\[L = \{x \in \{0,1\}^*: \text{存在一个证书}y, |y| = O(|x|^c), A(x,y) = 1\}. \]

目前不知道\(NP\)类在补运算下是否封闭. 定义\(\text{co-}NP\)为\(\overline{L} \in NP\)的语言\(L\)集合. 这相当于不知道是否有\(NP = \text{co-}NP\). 可知\(P \subseteq NP \cap \text{co-}NP\), 但不知道是否有\(P = NP \cap \text{co-}NP\).

对两个语言\(L_1\)和\(L_2\), 如果存在一个多项式时间可计算的函数\(f\), 使得\(x \in L_1\)当且仅当\(f(x) \in L_2\), 则称\(L_1\)可在多项式时间归约到\(L_2\), 记为\(L_1 \le_p L_2\).

NP完全类集合\(NPC\)定义为: 语言\(L \in NPC\), 当且仅当:

  1. \(L \in NP\).
  2. \(\forall L' \in NP, L' \le_p L\).

如果语言\(L\)满足性质2但不满足性质1, 称\(L\)为NP难的.

NP完全问题及归约证明

电路可满足性问题(CIRCUIT-SAT)

电路可满足性问题是第一个NP完全问题. 问题实例为给定一个单输出的由与、或、非门构成的布尔组合电路, 判断它是否为可满足的.

对任意NP问题\(L \in NP\), 可以将其多项式时间归约到电路可满足性问题中\(L \le_p \text{CIRCUIT-SAT}\).

布尔公式可满足性问题(SAT)

给定\(n\)个布尔变量, 由\(m\)个单输入或两输入的布尔连接词(与、或、非、蕴含等)连接为一个布尔公式, 公式中可以有括号规定优先级. SAT问题判断是否有一组变量赋值使布尔公式结果为真.

SAT问题是NP完全的, 可证明\(\text{CIRCUIT-SAT} \le_p \text{SAT}\).

3-CNF可满足性(3-CNF-SAT)

布尔公式为合取范式(CNF), 且每个子句为三个不同的文字或. 判断是否有一组变量取值使得布尔公式取值.

3-CNF-SAT问题为NP完全问题, 可证明\(\text{SAT} \le_p \text{3-CNF-SAT}\).

团问题(CLIQUE)

无向图\(G = (V, E)\)中的团为一个顶点子集, 其中每对顶点间均有边. 团问题形式定义为\(\text{CLIQUE} = \{<G, k>: G \text{中有一个规模为} k \text{的团}\}\).

团问题为NP完全的, 可证明\(\text{3-CNF-SAT} \le_p \text{CLIQUE}\).

顶点覆盖问题(VERTEX-COVER)

无向图\(G = (V, E)\)中的一个顶点覆盖为顶点子集, 使得子集中顶点覆盖了\(E\)中每条边. 问题形式定义为\(\text{VERTEX-COVER} = \{<G, k>: G \text{中有一个规模为} k \text{的顶点覆盖}\}\).

顶点覆盖问题为NP完全的, 可证明\(\text{CLIQUE} \le_p \text{VERTEX-COVER}\).

汉密顿回路问题(HAM-CYCLE)

对无向图\(G = (V, E)\), 汉密顿回路为一条经过每个顶点恰好一次的回路, 判断\(G\)中是否存在汉密顿回路.

汉密顿回路问题为NP完全的, 可证明\(\text{VERTEX-COVER} \le_p \text{HAM-CYCLE}\).

旅行商问题(TSP)

一个无向完全图\(G = (V, E)\), 两顶点之间的边有权值\(c_{ij}\), 找到一个总权值最低的汉密顿回路. TSP判定问题的形式定义为\(\text{TSP} = \{<G, c, k>: G \text{为一个无向图}, c \text{为权值矩阵, 判断} G \text{中是否有一个总权值至多为} k \text{的汉密顿回路}\}\).

旅行商问题为NP完全的, 可证明\(\text{HAM-CYCLE} \le_p \text{TSP}\).

子集和问题(SUBSET-SUM)

一个有限集\(S \subset \mathbb{N}\), 和一个目标和\(t\), 判断是否有一个子集\(S' \subseteq S\)使得\(S'\)中元素和为\(t\).

子集和问题为NP完全的, 可证明\(\text{3-CNF-SAT} \le_p \text{SUBSET-SUM}\).

posted @ 2023-06-07 11:27  Nobody_sh  阅读(49)  评论(0)    收藏  举报