本文给出基于分段加加速度的qp优化问题构造过程和仿真结果。其中,加加速度是优化变量,代价函数和约束条件考虑了安全、舒适和任务完成度。
基于分段加加速度的qp优化问题构造
变量定义
- 离散时刻点:\(t_i\in [0, K]\),其中,\(K\in Z^+\),\(t_0\)代表当前时刻,\(t_1...t_K\)代表未来时刻。
- 相邻时刻的时间间隔:\(dt_i=t_{i+1}-t_{i}, i\in[0, K-1]\).
- \(t_i\)时刻的车辆状态:位置\(s_i\in R\),速度\(\dot s_i\in R\),加速度\(\ddot s_i\in R\),\(i\in[0, K]\).
- \(t_0\)到\(t_{K-1}\)时刻对应的车辆分段加加速度:\(\dddot s_i \in R, i\in[0, K-1]\).
备注:分段加加速度的含义是在每段\(dt_i\)内,运动的加加速度\(\dddot s_i\)不变。
状态量计算
分段加加速度运动中的加加速度有三重含义:分段积分过程中作为常量;控制问题中作为控制量;优化问题中作为优化变量。具体的\(s_i,\dot s_i, \ddot s_i, \dddot s_i\)和\(dt_i\)关系如下图
![]()
参考《Optimal Trajectory Generation for Autonomous Vehicles Under Centripetal Acceleration Constraints for In-lane Driving Scenarios》
图片中\(t_{i}\)和\(t_{i+1}\)时刻的状态转移关系如下
\[\ddot s_{i+1} = \ddot s_i + \dddot s_i * dt_i \label{scalar_acc_trans} \tag{1}
\]
\[\dot s_{i+1} = \dot s_i +\ddot s_i dt_i + \dfrac{1}{2}\dddot s_i dt^2_i \label{scalar_vel_trans} \tag{2}
\]
\[s_{i+1} = s_i + \dot s_i dt_i + \dfrac{1}{2}\ddot s_i dt^2_i + \dfrac{1}{6}\dddot s_i dt^3_i \label{scalar_dis_trans} \tag{3}
\]
为了更方便地代入到二次优化问题中,公式\(\eqref{scalar_acc_trans}-\eqref{scalar_dis_trans}\)需要转换成矩阵形式如下
\[\ddot S = \ddot S_0 + A*T*\dddot S \label{mat_acc_trans} \tag{4}
\]
\[\dot S = \dot S_0 + AT\ddot S_0 + (ATBT+\dfrac{1}{2}ATT)\dddot S \label{mat_vel_trans} \tag{5}
\]
\[S = S_0 + AT\dot S_0 + (ATBT+\dfrac{1}{2}ATT)\ddot S_0 + (ATBTBT+\dfrac{1}{2}ATBTT + \dfrac{1}{2}ATTBT + \dfrac{1}{6}ATTT)\dddot S \label{mat_dis_trans} \tag{6}
\]
其中,
\[\dddot S = [\dddot s_0, \dddot s_1,...,\dddot s_{K-2},\dddot s_{K-1}]^T \label{eq_mat_sddd} \tag{7}
\]
\[\ddot S = [\ddot s_1, \ddot s_2,...,\ddot s_{K-1},\ddot s_{K}]^T \tag{8}
\]
\[\dot S = [\dot s_1, \dot s_2,...,\dot s_{K-1},\dot s_{K}]^T \tag{9}
\]
\[S = [s_1, s_2,...,s_{K-1},s_{K}]^T \tag{10}
\]
\[\ddot S_0 = [\ddot s_0,...,\ddot s_0]^T \in R^K \tag{11}
\]
\[\dot S_0 = [\dot s_0, ...,\dot s_0]^T \in R^K \tag{12}
\]
\[S_0 = [s_0, ...,s_0]^T \in R^K \tag{13}
\]
\[A = \begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K} \label{eq_mat_A} \tag{14}
\]
\[B = \begin{bmatrix}
0 & 0 & \dots & 0\\
1 & 0 & \dots & 0\\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K} \label{eq_mat_B} \tag{15}
\]
\[T = \begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K} \label{eq_mat_T} \tag{16}
\]
代价函数和边界计算
为了运动的安全、舒适和匹配(完成任务),需要构造代价函数,如下
\[f(\dddot S) = f_1(S, S_{ref}) + f_2(\dot S, \dot S_{ref}) + f_3(\ddot S, \ddot S_{ref}) + f_4(\dddot S, \dddot S_{ref}) \label{total_cost} \tag{17}
\]
其中,
\[f_1(S, S_{ref}) = (S-S_{ref})^TW_1(S-S_{ref}) \label{dis_cost_simple} \tag{18}
\]
\[f_2(\dot S, \dot S_{ref}) = (\dot S-\dot S_{ref})^TW_2(\dot S- \dot S_{ref}) \label{vel_cost_simple} \tag{19}
\]
\[f_3(\ddot S, \ddot S_{ref}) = (\ddot S-\ddot S_{ref})^TW_3(\ddot S-\ddot S_{ref}) \label{acc_cost_simple} \tag{20}
\]
\[f_4(\dddot S, \dddot S_{ref}) = (\dddot S-\dddot S_{ref})^TW_4(\dddot S-\dddot S_{ref}) \label{jerk_cost_simple} \tag{21}
\]
前两项\(f_1\)和\(f_2\)对应匹配和安全,后两项\(f_3\)和\(f_4\)对应舒适。向量\(S_{ref}, \dot S_{ref}, \ddot S_{ref},\dddot S_{ref}\in R^{K \times 1}\)代表参考项,表示期望的位置、速度、加速度和加加速度。矩阵\(W_1,W_2,W_3,W_4\in R^{K\times K}\)代表权重,权重值越大,状态量越接近参考值。
函数\(f_1(S, S_{ref})\)展开合并如下
\[f_1(S, S_{ref}) = \dddot S^TC^TW_1C\dddot S + 2D^TW_1C\dddot S + D^TW_1D \label{dis_cost} \tag{22}
\]
函数\(f_2(\dot S, \dot S_{ref})\)展开合并如下
\[f_2(\dot S, \dot S_{ref}) = \dddot S^T E^T W_2 E \dddot S + 2F^T W_2 E \dddot S + F^T W_2 F \label{vel_cost} \tag{23}
\]
函数\(f_3(\ddot S, \ddot S_{ref})\)展开合并如下
\[f_3(\ddot S, \ddot S_{ref}) = \dddot S^T M^T W_3 M \dddot S + 2 N^T W_3 M \dddot S + N^T W_3 N \label{acc_cost} \tag{24}
\]
函数\(f_4(\dddot S, \dddot S_{ref})\)展开合并如下
\[f_4(\dddot S, \dddot S_{ref}) = \dddot S^T P^T W_4 P \dddot S + 2 Q^T W_4 P \dddot S + Q^T W_4 Q \label{jerk_cost} \tag{25}
\]
其中,\(C=ATBTBT+\dfrac{1}{2}ATBTT+\dfrac{1}{2}ATTBT+\dfrac{1}{6}ATTT\),
\(D = S_0 + AT\dot S_0 + (ATBT+\dfrac{1}{2}ATT)\ddot S_0 - S_{ref}\),
\(E = ATBT+\dfrac{1}{2}ATT\),
\(F = \dot S_0 + AT\ddot S_0 - \dot S_{ref}\),
\(M = AT\),
\(N = \ddot S_0 - \ddot S_{ref}\),
\(P = I\),
\(Q = O - \dddot S_{ref}\),
\(I\in R^{K \times K}\)代表单位矩阵,
\(O \in R^{K \times K}\) 代表零向量 。
除了代价函数,还需要对\(S, \dot S, \ddot S, \dddot S\)的边界进行约束,如下
\[S_{low} \leq S \leq S_{upp} \label{dis_ineq} \tag{26}
\]
\[\dot S_{low} \leq \dot S \leq \dot S_{upp} \label{vel_ineq} \tag{27}
\]
\[\ddot S_{low} \leq \ddot S \leq \ddot S_{upp} \label{acc_ineq} \tag{28}
\]
\[\dddot S_{low} \leq \dddot S \leq \dddot S_{upp} \label{jerk_ineq} \tag{29}
\]
其中,\(\eqref{dis_ineq}\)对应纵向避障,\(\eqref{vel_ineq}\)对应纵向速度约束(弯道限速、交通指示牌限速、横向加速度约束限速),\(\eqref{acc_ineq}\)和\(\eqref{jerk_ineq}\)对应纵向加速度和加加速度约束(舒适和能力上下限)。
QP二次型构造
基于代价函数和边界约束,构造二次型问题,如下
\[\begin{align}
& minimize \space f(\dddot S) = \dfrac{1}{2}\dddot S^T H \dddot S + U^T \dddot S \label{qp_cost} \tag{30} \\
& subject \space to \space \space g(\dddot S) = G \dddot S \leq L \label{qp_constraints} \tag{31}
\end{align}
\]
具体推导如下
首先,将\(\eqref{dis_cost}-\eqref{jerk_cost}\)代入\(\eqref{total_cost}\),合并同类项可得
\[\begin{align}
f(\dddot S) =
& \dddot S^T C^T W_1 C \dddot S + 2D^T W_1 C \dddot S D^T W_1 D + \tag{32} \\
& \dddot S^T E^T W_2 E \dddot S + 2F^T W_2 E \dddot S + F^T W_2 F+ \notag \\
& \dddot S^T M^T W_3 M \dddot S + 2 N^T W_3 M \dddot S + N^T W_3 N+ \notag \\
& \dddot S^T P^T W_4 P \dddot S + 2Q^T W_4 P Q + Q^T W_4 Q \notag \\
=
& \dddot S^T(C^T W_1 C + E^T W_2 E + M^T W_3 M + P^T W_4 P)\dddot S + \notag \\
& 2(D^T W_1 C + F^T W_2 E + N^T W_3 M + Q^T W_4 P) \dddot S + \notag \\
& D^T W_1 D + F^T W_2 F + N^T W_3 N + Q^T W_4 Q \notag
\end{align}
\]
对于二次型问题,代价函数的常数项对优化结果没有影响,所以可以舍去常数项,则\(H\)和\(U\)分别如下
\[H = 2(C^T W_1 C + E^T W_2 E + M^T W_3 M + P^T W_4 P) \tag{33}
\]
\[U = 2(D^T W_1 C + F^T W_2 E + N^T W_3 M + Q^T W_4 P)^T \tag{34}
\]
然后,将\(\eqref{mat_acc_trans}-\eqref{mat_dis_trans}\)代入\(\eqref{dis_ineq}-\eqref{jerk_ineq}\),合并同类项可得
\[\left[
\begin{matrix}
-C \\
C \\
-E \\
E \\
-M \\
M \\
-P \\
P
\end{matrix}
\right] \dddot S \leq
\left[
\begin{matrix}
-S_{low} + D + S_{ref}\\
S_{upp} - D - S_{ref} \\
-\dot S_{low} + F + \dot S_{ref} \\
\dot S_{upp} - F - \dot S_{ref} \\
-\ddot S_{low} + N + \ddot S_{ref} \\
\ddot S_{upp} - N - \ddot S_{ref} \\
-\dddot S_{low} + Q + \dddot S_{ref} \\
\dddot S_{upp} - Q - \dddot S_{ref} \\
\end{matrix}
\right] \tag{35}
\]
进而得到\(G\)和\(L\)如下
\[G = \left[
\begin{matrix}
-C \\
C \\
-E \\
E \\
-M \\
M \\
-P \\
P
\end{matrix}
\right] \tag{36}
\]
\[L =
\left[
\begin{matrix}
-S_{low} + D + S_{ref}\\
S_{upp} - D - S_{ref} \\
-\dot S_{low} + F + \dot S_{ref} \\
\dot S_{upp} - F - \dot S_{ref} \\
-\ddot S_{low} + N + \ddot S_{ref} \\
\ddot S_{upp} - N - \ddot S_{ref} \\
-\dddot S_{low} + Q + \dddot S_{ref} \\
\dddot S_{upp} - Q - \dddot S_{ref} \\
\end{matrix}
\right] \tag{37}
\]
至此,关于速度规划的QP问题\(\eqref{qp_cost}-\eqref{qp_constraints}\)已构造完成,将其填入数值优化工具包matlab,即可获得最有速度序列。
仿真结果
仿真代码链接:https://github.com/PeiyaoShen/motion_planning/tree/main/const_piece_jerk
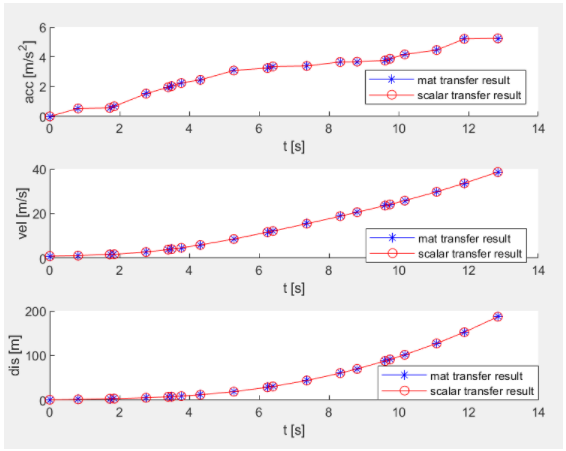
下图中的红色圆圈代表公式\(\eqref{scalar_acc_trans}-\eqref{scalar_dis_trans}\)的状态转移结果,蓝色星号代表公式\(\eqref{mat_acc_trans}-\eqref{mat_dis_trans}\)的状态转移结果。两者重叠说明了公式\(\eqref{mat_acc_trans}-\eqref{mat_dis_trans}\)的正确性。
![]()
下图是qp优化结果,可以看到通过增大距离项权重\(W_1\),左子图中opt更贴近ref,即距离优化结果更贴近距离参考。
![]()
附录
公式\(\eqref{mat_acc_trans}-\eqref{mat_dis_trans}\)的推导过程
公式\(\eqref{mat_acc_trans}\)的推导
由公式\(\eqref{scalar_acc_trans}\)显然可得公式\(\eqref{mat_acc_trans}\),公式\(\eqref{mat_acc_trans}\)中每项展开后如下
\[\begin{bmatrix}
\ddot s_1 \\
\ddot s_2 \\
\vdots \\
\ddot s_{K} \\
\end{bmatrix}_{K \times 1}
=
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1} \label{eq_acc_complicated} \tag{38}
\]
公式\(\eqref{mat_vel_trans}\)的推导
根据公式\(\eqref{scalar_vel_trans}\),可得
\[\begin{bmatrix}
\dot s_1 \\
\dot s_2 \\
\vdots \\
\dot s_{K} \\
\end{bmatrix}_{K \times 1}
=
\begin{bmatrix}
\dot s_0 \\
\dot s_0 \\
\vdots \\
\dot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\ddot s_0 \\
\ddot s_1 \\
\vdots \\
\ddot s_{K-1} \\
\end{bmatrix}_{K \times 1}
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1} \label{eq_explain1} \tag{39}
\]
上式中的每一行表示从0时刻开始用公式\(\eqref{scalar_vel_trans}\)做积分所得到的速度值。借助公式\(\eqref{eq_acc_complicated}\),公式\(\eqref{eq_explain1}\)中的向量\([\ddot s_0, \ddot s_1, ..., \ddot s_{K-1}]^T\)可表示为
\[\begin{bmatrix}
\ddot s_0 \\
\ddot s_1 \\
\ddot s_2 \\
\vdots \\
\ddot s_{K-1} \\
\end{bmatrix}_{K \times 1}
=
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1} \label{eq_explain2} \tag{40}
\]
向量\([\ddot s_0, \ddot s_1, ..., \ddot s_{K-1}]^T\)的第2~K-1行算式用公式\(\eqref{eq_acc_complicated}\)的第1~K-1表示,向量\([\ddot s_0, \ddot s_1, ..., \ddot s_{K-1}]^T\)的第1行用\(\ddot s_0 + 0\)表示。
将公式\(\eqref{eq_explain2}\)代入\(\eqref{eq_explain1}\)可得下式
\[\begin{bmatrix}
\dot s_1 \\
\dot s_2 \\
\vdots \\
\dot s_{K} \\
\end{bmatrix}_{K \times 1}
=
\begin{bmatrix}
\dot s_0 \\
\dot s_0 \\
\vdots \\
\dot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\left(
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1}
\right)
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1} \label{eq_explain3} \tag{41}
\]
对上式合并同类项,可得
\[\begin{bmatrix}
\dot s_1 \\
\dot s_2 \\
\vdots \\
\dot s_{K}
\end{bmatrix}_{K\times1}
=
\begin{bmatrix}
\dot s_0 \\
\dot s_0 \\
\vdots \\
\dot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\left(
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\right)
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1}
\label{eq_explain6} \tag{42}
\]
用\(\eqref{eq_mat_sddd}-\eqref{eq_mat_T}\)中的符号替代上式中对应的矩阵,即是公式\(\eqref{mat_vel_trans}\).
公式\(\eqref{mat_dis_trans}\)的推导
根据公式\(\eqref{scalar_dis_trans}\),可得
\[\begin{bmatrix}
s_1 \\
s_2 \\
\vdots \\
s_{K} \\
\end{bmatrix}_{K \times 1}
=
\begin{bmatrix}
s_0 \\
s_0 \\
\vdots \\
s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dot s_0 \\
\dot s_1 \\
\vdots \\
\dot s_{K-1} \\
\end{bmatrix}_{K \times 1}
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\ddot s_0 \\
\ddot s_1 \\
\vdots \\
\ddot s_{K-1}
\end{bmatrix}_{K \times 1}
+
\dfrac{1}{6}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1} \label{eq_explain4} \tag{43}
\]
上式中的每一行表示从0时刻开始用公式\(\eqref{scalar_dis_trans}\)做积分所得到的位置值。借助公式\(\eqref{eq_explain6}\),公式\(\eqref{eq_explain4}\)中的向量\([\dot s_0, \dot s_1, ..., \dot s_{K-1}]^T\)可表示为
\[\begin{bmatrix}
\dot s_0 \\
\dot s_1 \\
\vdots \\
\dot s_{K-1}
\end{bmatrix}_{K\times1}
=
\begin{bmatrix}
\dot s_0 \\
\dot s_0 \\
\vdots \\
\dot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\left(
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
+
\dfrac{1}{2}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\right)
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1}
\label{eq_explain7} \tag{44}
\]
向量\([\dot s_0, \dot s_1, ..., \dot s_{K-1}]^T\)的第2~K-1行算式用公式\(\eqref{eq_explain6}\)的第1~K-1表示,向量\([\dot s_0, \dot s_1, ..., \dot s_{K-1}]^T\)的第1行用\(\dot s_0 + 0\)表示。
将公式\(\eqref{eq_explain2}\)和\(\eqref{eq_explain7}\)代入\(\eqref{eq_explain4}\)可得下式
\[\begin{bmatrix}
s_1 \\
s_2 \\
\vdots \\
s_{K} \\
\end{bmatrix}_{K \times 1}
=
\begin{bmatrix}
s_0 \\
s_0 \\
\vdots \\
s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\left(
\begin{bmatrix}
\dot s_0 \\
\dot s_0 \\
\vdots \\
\dot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\left(
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
+
\dfrac{1}{2}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\right)
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1}
\right)
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\left(
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1}
\right)
+
\dfrac{1}{6}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K \times 1} \label{eq_explain8} \tag{45}
\]
对上式合并同类项,可得
\[\begin{bmatrix}
s_1 \\
s_2 \\
\vdots \\
s_{K} \\
\end{bmatrix}_{K \times 1}
=
\begin{bmatrix}
s_0 \\
s_0 \\
\vdots \\
s_{0}
\end{bmatrix}_{K \times 1}
+
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
\dot s_0 \\
\dot s_0 \\
\vdots \\
\dot s_{0}
\end{bmatrix}_{K \times 1}
+
\left(
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\right)
\begin{bmatrix}
\ddot s_0 \\
\ddot s_0 \\
\vdots \\
\ddot s_{0}
\end{bmatrix}_{K \times 1}
+
\left(
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
+
\dfrac{1}{2}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
0 & \dots & \dots & 0 \\
1 & 0 & \dots & 0 \\
\vdots & \ddots & \ddots & \vdots \\
1 & \dots & 1 & 0
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
+
\dfrac{1}{6}
\begin{bmatrix}
1 & 0 & \dots & 0 \\
1 & 1 & \ddots & \vdots \\
\vdots & \vdots & \ddots & 0 \\
1 & 1 & \dots & 1
\end{bmatrix}_{K \times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\begin{bmatrix}
dt_0 & 0 & \dots & 0 \\
0 & dt_1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & 0 \\
0 & \dots & 0 & dt_{K-1}
\end{bmatrix}_{K\times K}
\right)
\begin{bmatrix}
\dddot s_0 \\
\dddot s_1 \\
\vdots \\
\dddot s_{K-1}
\end{bmatrix}_{K\times 1}
\label{eq_explain9} \tag{46}
\]
用\(\eqref{eq_mat_sddd}-\eqref{eq_mat_T}\)中的符号替代上式中对应的矩阵,即是公式\(\eqref{mat_dis_trans}\).
至此公式\(\eqref{mat_acc_trans}-\eqref{mat_dis_trans}\)的推导过程描述完毕。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号