基于粒子群优化(PSO)算法与PID神经网络结合的系统控制算法
一、算法原理与架构设计
1. 系统架构
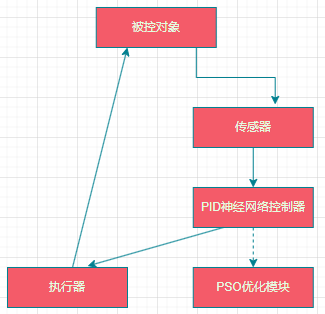
2. PID神经网络结构
- 输入层:接收误差信号 \(e(k)\)和误差变化率 \(Δe(k)\)
- 隐含层:包含比例元、积分元、微分元神经元
- 输出层:生成PID参数 \(K_p,K_i,K_d\)
3. PSO优化流程
-
粒子编码:将 \(K_p,K_i,K_d\) 编码为3维粒子位置
-
适应度函数:基于控制误差设计(如ITAE准则)
-
参数更新:
![]()
二、MATLAB代码
1. 环境配置
addpath(genpath('Neural Network Toolbox'));
addpath(genpath('Global Optimization Toolbox'));
2. 核心代码实现
%% 系统模型定义
sys = tf(400, [1,50,0]); % 被控对象传递函数
dsys = c2d(sys, 0.01, 'z'); % 离散化
%% PSO参数设置
nPop = 30; % 粒子数量
maxIter = 100; % 最大迭代次数
w = 0.729; % 惯性权重
c1 = 1.494; % 个体学习因子
c2 = 1.494; % 群体学习因子
%% PID神经网络初始化
net = feedforwardnet([5 3]); % 隐含层结构
net.trainParam.epochs = 100; % 训练次数
%% PSO优化过程
lb = [0.1, 0.01, 0.01]; % 参数下限
ub = [100, 10, 10]; % 参数上限
[gbest, fval] = particleswarm(@(x) fitnessFunc(x,net,sys),3,lb,ub);
%% 优化后PID参数
Kp = gbest(1); Ki = gbest(2); Kd = gbest(3);
%% 闭环控制仿真
pid = pidtune(sys, 'PID', [Kp Ki Kd]);
T = 0:0.01:10;
[y,t] = step(pid*sys, T);
plot(t,y); grid on;
3. 适应度函数
function error = fitnessFunc(x,net,sys)
% 解码参数
Kp = x(1); Ki = x(2); Kd = x(3);
% 构建PID控制器
pid = pidtune(sys, 'PID', [Kp Ki Kd]);
% 闭环仿真
[y,t] = step(pid*sys, 0:0.01:10);
% 计算ITAE指标
error = trapz(t, t.*abs(y - 1));
end
三、优化
1. 参数空间约束
-
工程经验约束:根据系统增益和延迟特性限定参数范围
% 开环增益约束(Rule.1) Kp_max = 1.5*sys.OpenLoopGain; -
动态比例约束:根据系统延迟调整Ki/Kd比例
tau = 0.5; % 延迟时间 Ki_max = Kp*tau/0.1; % Rule.2
2. 收敛性改进
-
自适应惯性权重:
w = w_max - (w_max - w_min)*(iter/maxIter)^2; -
动态学习因子:
c1 = 2.5 - 0.5*(iter/maxIter); c2 = 1.5 + 0.5*(iter/maxIter);
3. 多目标优化
% 多目标适应度函数
fitness = @(x) [ITAE(x), ISE(x)]; % 多目标向量
options = optimoptions('particleswarm','SwarmSize',50,'Display','iter');
[gbest,fval] = particleswarm(fitness,3,lb,ub,options);
参考代码 基于pso算法优化的PID神经网络的系统控制算法 www.youwenfan.com/contentcnk/78835.html
四、注意事项
- 参数初始化:建议使用拉丁超立方采样
- 边界处理:采用反射边界策略
- 早停机制:设置适应度变化阈值(如<1e-6)
- 实时性保障:控制周期需>10倍计算时间


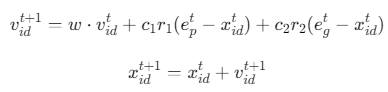

 浙公网安备 33010602011771号
浙公网安备 33010602011771号