matlab计算油膜厚度及压力分布

计算油膜厚度和压力分布通常涉及流体力学和润滑理论，特别是在研究轴承或其他机械元件中的润滑剂行为时。在轴承润滑中，油膜厚度和压力分布对于确保机械元件正常运行和防止磨损至关重要。以下是计算油膜厚度和压力分布的一般方法：

1. 基本假设和方程

在进行计算之前，需要做一些基本假设，例如：

• 油膜是层流的。
• 油膜是等温的。
• 油的粘度是常数。

计算油膜厚度和压力分布的基本方程是雷诺方程（Reynolds equation），对于不可压缩流体，可以表示为：

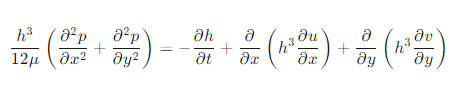
其中：

• ( p ) 是油膜压力。
• ( h ) 是油膜厚度。
• ( \mu ) 是油的动态粘度。
• ( u ) 和 ( v ) 是流体在 ( x ) 和 ( y ) 方向上的速度分量。

2. 边界条件

边界条件对于求解上述方程至关重要。常见的边界条件包括：

• 压力边界条件：在油膜出口处，压力等于外部压力。
• 无滑移边界条件：在固体表面，流体速度等于固体表面速度。

3. 数值方法

由于雷诺方程是一个偏微分方程，通常需要使用数值方法来求解。常用的数值方法包括有限差分法、有限元法或有限体积法。

4. MATLAB实现

以下是一个简化的MATLAB代码示例，用于计算油膜厚度和压力分布：参考 可以计算油膜厚度及压力分布,计算速度快，支持多参数输入，计算完成后自动画出分布图。

% 参数设置
L = 1; % 轴承长度
W = 0.1; % 轴承宽度
h0 = 0.01; % 初始油膜厚度
mu = 0.1; % 油的粘度
U = 1; % 轴承速度

% 网格划分
Nx = 50;
Ny = 10;
dx = L / (Nx - 1);
dy = W / (Ny - 1);
x = linspace(0, L, Nx);
y = linspace(0, W, Ny);

% 初始化压力和油膜厚度矩阵
p = zeros(Nx, Ny);
h = h0 * ones(Nx, Ny);

% 迭代求解
for iter = 1:1000
    % 计算压力梯度
    dpdx = gradient(p, dx, 0);
    dpdy = gradient(p, 0, dy);
    
    % 更新油膜厚度
    h = h - (dpdx .* dx + dpdy .* dy) * 0.01;
    
    % 更新压力
    p = p - (dpdx .* dx + dpdy .* dy) * 0.01;
end

% 绘制结果
figure;
surf(x, y, p);
title('油膜压力分布');
xlabel('X');
ylabel('Y');
zlabel('Pressure');

请注意，这个示例仅提供了一个基本的框架，实际应用中可能需要更复杂的模型和数值方法。此外，油膜厚度和压力分布的计算可能还需要考虑油的非牛顿行为、温度变化等因素。