动态规划DP

---

前言：

因为在练习算法题时遇到了经典的背包问题，而解决这个问题的最优方法是动态规划

为了更多的了解动态规划，结合网上资料和个人理解系统地整理了一份资料

可能对于部分人来说学习一个方法只要知道怎么用就行，而不去管这个方法的概念原理等，但是对于动态规划，最主要的就是其概念和思路，所以建议仔细地了解一下概念

---

什么是动态规划？

动态规划是一种方法：把原来的问题分解为 相对简单的子问题 从而通过求解子问题来求解原问题的方法，是一种用来解决一类 最优化问题 的算法思想。

动态规划有两个写法：

• 递归 —— 重叠子问题
• 递推 —— 最优子结构

重叠子问题：动态规划会将每个求解过的子问题的解 记录 下来，这样当下一次碰到同样的子问题时，就可以 直接使用 之前记录的结果，而不是重复计算。

最优子结构：动态规划将一个复杂的问题 分解 成若干个子问题，通过 综合 子问题的最优解来得到原问题的最优解。

重叠子问题：

记录子问题的解，来避免下次遇到相同的子问题时的重复计算。

以斐波那契数列为例：

已知 F₀ = 1, F₁ = 1, F₂ = 2, F₃ = 3, 求 F₁₀₀ 的值

计算斐波那契数列的状态转移方程为：F(n) = F(n-1) + F(n-2)

这里我们直接用 C语言 写出代码

#include<stdio.h>

void F(int n)
{
    if(n == 0 || n == 1) return 1;
    else return F(n-1) + F(n-2);
}

int main()
{
    int n = 100;
    answer = F(n);
    print("%d", answer);
    return 0;
}

可以通过计算得到代码的 时间复杂度为 O(2ⁿ) ,“多看一眼都会爆炸~~”

我们通过图来分析一下递归的过程：

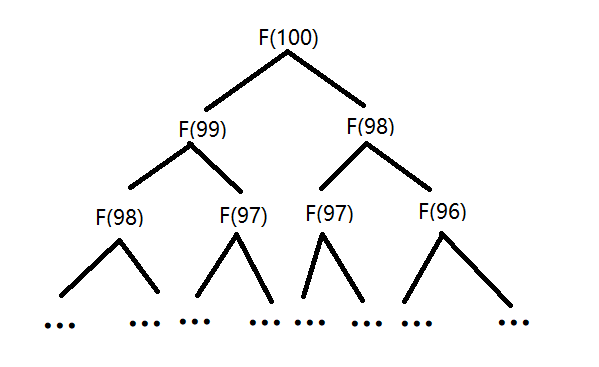
从图上我们可以了解到一个很重要的信息：

几乎每个数字都被 重复计算 ，图上可见的 F(98), F(97) 就已经被计算了两次，如果我们求的 n 不是100，是更大的数，例如求 F_1000000 ，这样大量的重复计算会大大增加时间上的消耗

为了 避免重复计算 ，我们可以 记录已经计算过的结果 ，在下次计算时直接返回这个结果

具体代码如下：

#include<stdio.h>

int dp[100] = {-1}; // 用数组 dp 记录计算过的数字，先初始化数组

void F(int n)
{
    if(n == 0 || n == 1) return 1;
    if(dp[n] != -1) return dp[n];
	else
    {
		dp[n] = F(n-1) + F(n-2);	//记录
		return dp[n];
    }
}

int main()
{
    int n = 100;
    answer = F(n);
    print("%d", answer);
    return 0;
}

通过上述方法可以将时间复杂度从 O(2ⁿ) 降至 O(n)

这就是俗称 “带备忘录的递归解法（自顶向下）”

最优子结构：

如果一个问题的最优解可以由其子问题的最优解有效地构造出来，那么称这个问题拥有 最优子结构 ，最优子结构保证了动态规划中原问题的最优解可以由子问题的最优解推导而来。

以青蛙跳台阶为例：

有一只青蛙想跳台阶，青蛙一次可以跳1级台阶或者2级台阶，求青蛙跳到第100级台阶时一共有多少中跳法

青蛙跳到第一级台阶只有一种跳法即跳1级（最优答案）

青蛙跳到第二级台阶有两种跳法即，直接跳2级到第二级台阶或先跳1级到第一级台阶然后再跳1级到第二级台阶（最优答案）

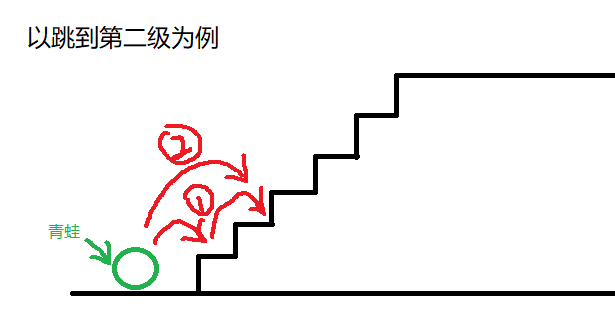
如果想跳跳到第三级台阶，分析一下，青蛙如果要跳到第三级台阶 只有两种跳法 ，从第一级跳2级到第三级台阶，或第二级跳1级台阶到第三级(因为青蛙只能跳1级或者2级)，则如果想跳到第三级只需要把 **跳到第一级台阶的跳法和跳到第二级台阶的跳法加起来 **即可

可得：f[3] = f[2] + f[1] 推出状态转移方程：f[n] = f[n-1] + f[n-2]

同样用 C语言 写出代码：

#include<stdio.h>

int main()
{
    int f[100] = {0};
    for(int i = 3; i <= 100; i++)
    {
        f[i] = f[i-1] + f[i-2];
    }
    print("%d", f[100]);
    return 0;
}

可以直接看出时间复杂度为 O(n)

从最下面算到最上面，即从 f(3) 算到 f(100) ，并且从最下面开始算出来的结果都是最优解，不断向上算出最优解，俗称 “自底向上的动态规划”

动态规划解题：

什么时候使用动态规划：

如果要求一个问题的 最优解（通常是最大值或者最小值或次数），而且该问题能够 分解成若干个子问题 ，并且小问题之间也存在重叠的子问题，则考虑采用动态规划。

比如一些经典场景，最大子序列和、零钱兑换、最长递增子序列、背包问题、航线问题等等

解题思路：

1. 穷举分析

   分析所有可能出现的情况

2. 确定边界

   根据分析情况找到边界，如青蛙跳台阶的边界就是跳第一个台阶的跳法和跳第二个台阶的跳法

3. 状态转移方程

   通过分析出来的情况，得出状态转移方程（如 f[n] = f[n-1] + f[n-2]）

总结：

动态规划 的计算方式有 ”自顶向下“ 和 ”自底向上“ 两种，都是从边界开始向上得到目标问题的解。也就是说，它总是会考虑 **所有子问题 **，并选择继承能得到最优结果的那个，对暂时没有被继承的子问题，由于重叠子问题的存在，后期可能会再次考虑它们，因此还有机会成为全局最优的一部分，不需要放弃。

网上有个比较流行的例子：

A ： "1+1+1+1+1+1+1+1 =？"

A ： "上面等式的值是多少"

B ： 计算 "8"

A : 在上面等式的左边写上 "1+" 呢？

A : "此时等式的值为多少"

B : 很快得出答案 "9"

A : "你怎么这么快就知道答案了"

A : "只要在8的基础上加1就行了"

A : "所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"

把这个例子放在最后而不是开头是希望不要把动态规划想复杂化了，了解动态规划的具体后想简单一点并且更好的运用

01背包：

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 v_i，价值是 w_i。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 v_i ,w_i 用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤10000
0<v_i,w_i≤1000

输入样例:

4 5
1 2
2 4
3 4
4 5

输出样例：

8

解决思路：

这里直接提供解决方法，具体实现过程可以自行思考

用一个2维数组来代表背包中已经装的物品以及背包的容积还有总价值

V[i][j] i 代表前 i 个物品， j 代表背包的容积，V[i][j] 代表此时背包物品 最佳组合 的价值

01背包指的是第 i 个物品只有选和不选两种情况

在面对第 i 个物品时，有两种可能：

• 包的容量比该商品体积小，装不下，此时的价值与前i-1个的价值是一样的，即V(i,j)=V(i-1,j)；
• 还有足够的容量可以装该商品，但装了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，即V[i,j]=max(V[i-1,j]，V[i-1,j-v(i)]+w(i))

=>通过这个可能可以得出关系式：

• j<w(i) V[i,j]=V[i-1,j]
• j>=w(i) V[i,j]=max(V[i-1,j]，V[i-1,j-v(i)]+w(i))

这里具体说明一下 为什么会用这种方法来求解 ：

如果要递推到 V[i,j] 这一个状态有几种途经

1. 第i件商品没有装进去

   没有装进去即 V[i,j] = V[i-1,j]

2. 是第i件商品装进去了

   装进去了，我们要根据装入之前的状态来计算（最优），而装入之前的 最优 状态为 V[i-1,j-v(i)] ,这个 最优 理解可以这样想，我们要使得第 i 件物品装入背包时 刚好装满 ，就选择没有装入第 i 件物品且背包容量刚好少 v(i) 的情况，即 V[i-1,j-v(i)]

V[i,j] 的状态只有这两种情况，然后将这两种情况的背包价值进行对比，选择价值最大 的结果填入 V[i,j]

初始化的表如图：

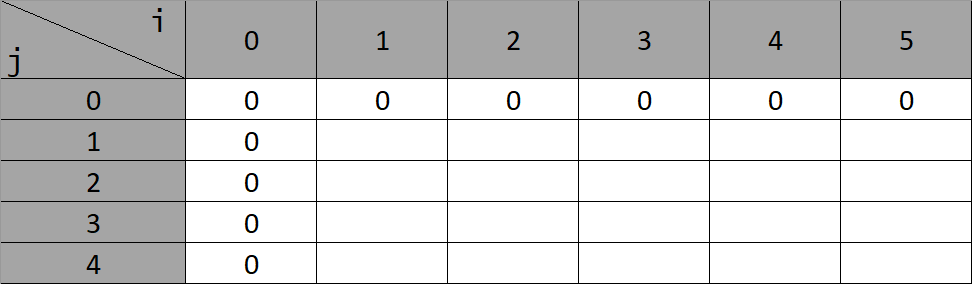
按所定义的方法填入后的表如图：

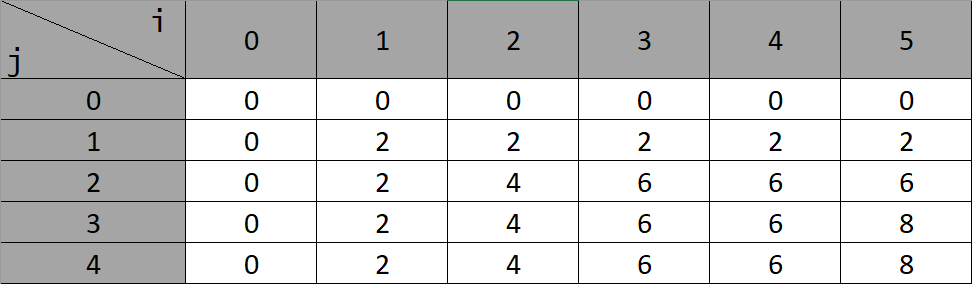
实现代码：

using namespace std;

const int N = 1005;
int n, m, v[N], w[N];
int f[N][N];


int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

	for (int i = 1; i <= n; i++)
		for (int j = 0; j <= m; j++)
		{	
            if(j < v[i])
				f[i][j] = f[i - 1][j];
			if (j >= v[i])
				f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
		}
	int res = 0;
	for (int i = 0; i <= m; i++) res = max(res, f[n][i]);
	cout << res << endl;
	return 0;
}