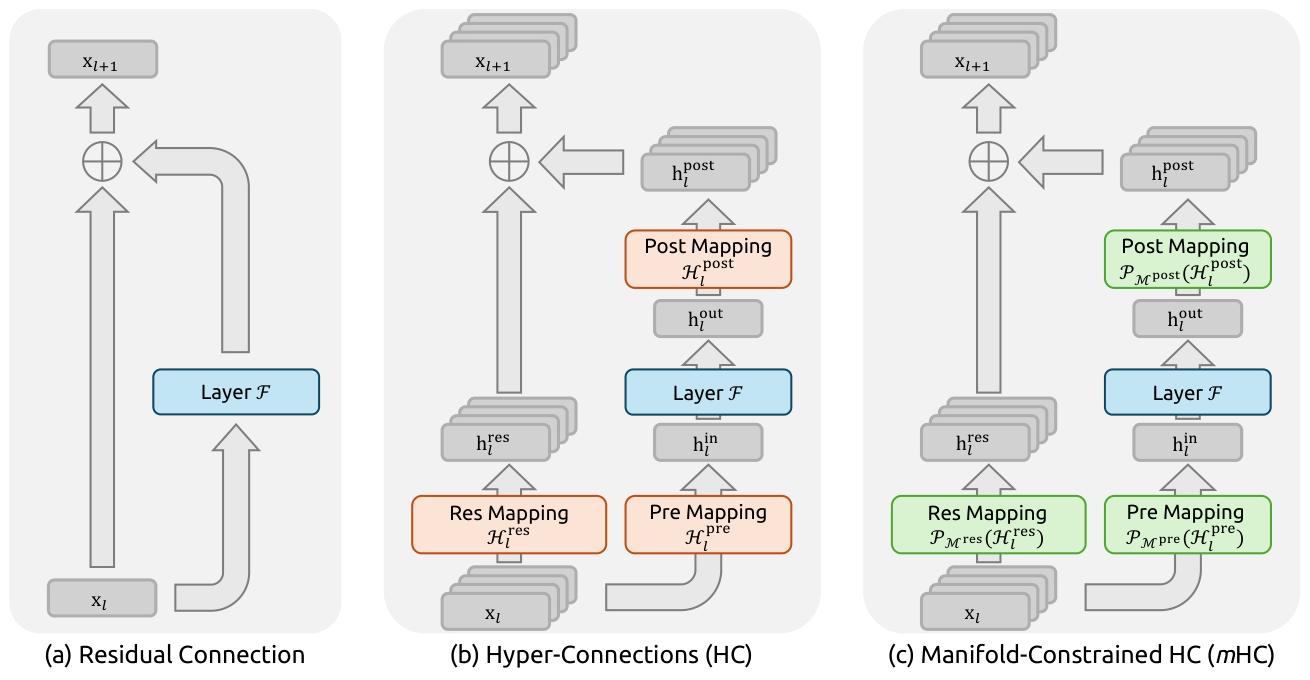
流形约束超连接（mHC）：Manifold-Constrained Hyper-Connections

Deepseek这篇论文核心是给深度学习模型的“残差连接”做了个优化升级，解决了原有方案的稳定性和效率问题：

先搞懂背景：什么是“残差连接”？

深度学习模型（比如大语言模型、图像识别模型）里，“残差连接”是个基础操作——就像给信号开了条“绿色通道”，让浅层的信息能直接传到深层，不用绕远路。这样能避免模型训练时出现“信号消失”或“信号爆炸”，让深层模型能稳定训练。

原来的残差连接很简单：深层输出 = 浅层输入 + 深层计算结果。后来有人提出了“超连接（HC）”，把这条“绿色通道”拓宽了（比如原来1条流，现在变成4条并行流），还加了些可学习的连接规则，想让信息传递更灵活，提升模型性能。

但“超连接（HC）”有两大问题：

1. 训练不稳定：原来的残差连接能保证“信号强度不变”（比如浅层信号传到深层还是原来的量级），但HC的连接规则是“无约束”的——多条流的信号混在一起时，容易出现有的信号越传越强（爆炸）、有的越传越弱（消失），模型训练到后期就会“崩掉”（比如损失值突然飙升）。
2. 效率低：通道拓宽后，模型要处理更多数据，内存读取、设备间通信的成本都涨了，训练速度变慢，还特别占显存。

这篇论文的解决方案：流形约束超连接（mHC）

简单说就是给HC的“无约束连接”加了个“规矩”，再优化了底层运行逻辑，既保留HC的性能优势，又解决了它的毛病。

1. 核心规矩：给连接加“流形约束”

论文把HC里的连接规则（一个矩阵），强行限制在一个叫“双随机矩阵”的“框架（流形）”里。这个框架有个关键特点：

• 矩阵的每行、每列加起来都等于1，而且所有元素都是非负数；
• 这样一来，多条流的信号混在一起时，总强度能保持不变（不会爆炸也不会消失），就像把信号“平均分配”后再传递，稳定性直接拉满；
• 而且多个这样的矩阵叠在一起用，依然能保持这个特性，深层模型也能稳定训练。

为了实现这个约束，论文用了一个叫“Sinkhorn-Knopp”的算法，相当于给连接规则做了个“标准化”，让它必须遵守上面的规矩。

2. 配套优化：解决效率问题

光稳定还不够，得让模型跑得不慢、不费资源：

• 合并计算步骤：把多个零散的计算操作整合在一起，减少内存读取次数（比如原来要读3次数据，现在1次搞定）；
• 选择性重计算：训练时不保存所有中间结果，需要时再临时计算，省显存；
• 优化通信逻辑：多设备并行训练时，让数据传输和计算能同时进行，减少等待时间。

最后看效果：

• 稳定性：原来的HC训练到12000步左右就会崩，mHC能一直稳定训练，梯度和损失值都很平稳；
• 性能：在8个下游任务（比如数学推理、阅读理解、常识问答）上，mHC比原来的HC和基础模型都强，尤其是推理类任务提升明显；
• 效率：虽然加了约束和优化，但训练时只多了6.7%的时间开销，几乎不影响速度，还能支持更大规模的模型训练（比如270亿参数的模型）。

总结一下：

这篇论文就是给深度学习模型的“信息绿色通道”做了俩改进：

1. 给通道的连接规则定了个“规矩”，避免信号乱飘导致训练崩溃；
2. 优化了通道的运行逻辑，让它又快又省资源。

最终实现了“更稳、更强、更快”的目标，还能适配更大规模的模型，给后续大模型的架构设计提供了新思路。

---

mHC（流形约束超连接）的核心公式围绕“残差映射的流形约束”“映射参数计算”和“单层传播逻辑”展开，以下是关键公式的完整呈现、通俗解释及逻辑关联，全程避开复杂术语堆砌：

一、核心公式汇总（按逻辑顺序）

1. 单层传播公式（mHC的核心运行逻辑）

继承HC的多流残差框架，新增流形约束后的最终传播规则：
\( x_{l+1} = \mathcal{P}_{\mathcal{M}^{res}}(\mathcal{H}_{l}^{res}) \cdot x_{l} + \mathcal{H}_{l}^{post\top} \cdot \mathcal{F}\left(\mathcal{H}_{l}^{pre} \cdot x_{l}, \mathcal{W}_{l}\right) \tag{核心传播式} \)

2. 流形约束定义（给残差映射加“规矩”）

将残差映射 \(\mathcal{H}_{l}^{res}\) 投影到“双随机矩阵流形” \(\mathcal{M}^{res}\) 的约束条件：
\( \mathcal{P}_{\mathcal{M}^{res}}(\mathcal{H}_{l}^{res}) := \left\{ \mathcal{H}_{l}^{res} \in \mathbb{R}^{n \times n} \mid \mathcal{H}_{l}^{res} \cdot 1_n = 1_n,\ 1_n^\top \cdot \mathcal{H}_{l}^{res} = 1_n^\top,\ \mathcal{H}_{l}^{res} \geq 0 \right\} \tag{约束条件式} \)

3. 映射参数计算（怎么得到符合约束的映射矩阵）

先通过输入特征计算原始映射，再通过激活/算法施加约束：
\( \begin{cases} \vec{x}_l' = \text{RMSNorm}(\vec{x}_l) \\ \tilde{\mathcal{H}}_{l}^{pre} = \alpha_{l}^{pre} \cdot (\vec{x}_l' \cdot \varphi_{l}^{pre}) + b_{l}^{pre} \\ \tilde{\mathcal{H}}_{l}^{post} = \alpha_{l}^{post} \cdot (\vec{x}_l' \cdot \varphi_{l}^{post}) + b_{l}^{post} \\ \tilde{\mathcal{H}}_{l}^{res} = \alpha_{l}^{res} \cdot \text{mat}(\vec{x}_l' \cdot \varphi_{l}^{res}) + b_{l}^{res} \end{cases} \tag{原始映射计算式} \)
\( \begin{cases} \mathcal{H}_{l}^{pre} = \sigma(\tilde{\mathcal{H}}_{l}^{pre}) \\ \mathcal{H}_{l}^{post} = 2\sigma(\tilde{\mathcal{H}}_{l}^{post}) \\ \mathcal{H}_{l}^{res} = \text{Sinkhorn-Knopp}(\tilde{\mathcal{H}}_{l}^{res}) \end{cases} \tag{约束施加式} \)

二、公式通俗解释（逐个拆解，用“通道”类比）

先明确核心前提：mHC把原来的“单条残差通道”拓宽成 \(n\) 条并行通道（比如 \(n=4\)），\(\mathcal{H}_{l}^{pre}\)（输入映射）、\(\mathcal{H}_{l}^{post}\)（输出映射）、\(\mathcal{H}_{l}^{res}\)（残差映射）是控制这 \(n\) 条通道“信息进出、内部混合”的规则。

1. 核心传播公式：mHC的“信息传递逻辑”

• 符号含义：
  • \(x_l\)：第 \(l\) 层的输入（\(n \times C\) 维度，可理解为“\(n\) 条通道，每条通道有 \(C\) 个特征”）；
  • \(x_{l+1}\)：第 \(l\) 层的输出（和输入维度一致，保证通道结构不变）；
  • \(\mathcal{P}_{\mathcal{M}^{res}}(\mathcal{H}_{l}^{res})\)：被约束后的残差映射（核心改进点，原来HC的 \(\mathcal{H}_{l}^{res}\) 无约束）；
  • \(\mathcal{F}(\cdot)\)：当前层的核心计算（比如Transformer的注意力+FFN，和原残差连接一致）；
  • \(\mathcal{H}_{l}^{pre}\)：输入映射（把 \(n\) 条通道的特征“汇总”成1条，给 \(\mathcal{F}\) 计算）；
  • \(\mathcal{H}_{l}^{post}\)：输出映射（把 \(\mathcal{F}\) 的计算结果“拆分”回 \(n\) 条通道，和残差信息合并）。
• 通俗理解：
  第 \(l\) 层的输出 = （约束后的残差映射 × 输入通道信息） + （输出映射 × 核心计算结果）
  相当于：\(n\) 条通道的原始信息，先按“规矩”混合传递，再加上核心计算的新信息，最终形成下一层的输入——既保留多通道的灵活性，又不打乱信息强度。

2. 约束条件公式：给残差映射定“规矩”

• 符号含义：
  • \(1_n\)：全1向量（长度为 \(n\)，比如 \(n=4\) 时就是 \([1,1,1,1]\)）；
  • \(\mathcal{H}_{l}^{res} \cdot 1_n = 1_n\)：残差映射的“每行加起来等于1”；
  • \(1_n^\top \cdot \mathcal{H}_{l}^{res} = 1_n^\top\)：残差映射的“每列加起来等于1”；
  • \(\mathcal{H}_{l}^{res} \geq 0\)：残差映射的所有元素都是非负数。
• 通俗理解：
  原来HC的残差映射是“随心所欲”的（比如某条通道的信息被放大100倍，另一条被缩小到0），而mHC给它加了3个限制：
  1. 每条通道的信息“分配比例”总和为1（比如通道1的信息分给下一层4条通道的比例是 \(0.3,0.2,0.4,0.1\)，加起来=1）；
  2. 每列加起来为1（保证下一层每条通道收到的信息总和不超标）；
  3. 没有负向分配（不会出现“抵消信息”的情况）。
     这就像给通道信息传递加了“流量控制器”，避免有的通道信息爆炸、有的消失。

3. 映射参数计算：怎么得到“守规矩”的映射矩阵

• 第一步：计算原始映射（原始映射计算式）

  • \(\vec{x}_l\)：把输入 \(x_l\)（\(n \times C\)）拉成1维向量（方便统一计算）；
  • \(\text{RMSNorm}\)：归一化操作（让输入特征的量级稳定，避免计算混乱）；
  • \(\varphi_{l}^{pre}/\varphi_{l}^{post}/\varphi_{l}^{res}\)：可学习的权重矩阵（模型自己学“怎么汇总/拆分/混合通道信息”）；
  • \(\alpha\) 和 \(b\)：缩放系数和偏置（微调映射的强度，让模型更灵活）；
  • \(\text{mat}(\cdot)\)：把1维向量重塑成 \(n \times n\) 矩阵（因为残差映射是控制 \(n\) 条通道的混合，需要矩阵形式）。

• 第二步：施加约束（约束施加式）

  • \(\sigma(\cdot)\)：Sigmoid函数（把原始输入映射/输出映射的结果压缩到0~1之间，保证“分配比例”合理）；
  • \(2\sigma(\cdot)\)：把输出映射的范围扩大到0~2（给输出信息多一点调节空间，不影响稳定性）；
  • \(\text{Sinkhorn-Knopp}(\cdot)\)：核心算法（把原始残差映射转换成“双随机矩阵”）。
  • 通俗理解：
    先通过输入特征算出“初步的通道控制规则”，再通过Sigmoid和Sinkhorn-Knopp算法“修正”这些规则，让它们满足前面说的约束条件——相当于先画个草稿，再按规矩修改成合规的最终方案。

三、核心逻辑总结

mHC的公式本质是“先拓宽通道（继承HC），再给通道加约束（核心创新），最后高效计算约束后的映射（工程优化）”：

1. 用“多通道”提升信息传递灵活性（保留HC的优势）；
2. 用“双随机矩阵约束”解决通道信息乱飘的问题（解决HC的不稳定性）；
3. 用Sigmoid和Sinkhorn-Knopp算法实现约束（让规则可学习、可落地）；
4. 最终通过核心传播公式，实现“稳定且灵活”的信息传递，让大模型能规模化训练且性能更好。

---

Sinkhorn-Knopp 算法：通俗解释与核心作用

Sinkhorn-Knopp 算法是 mHC 实现“残差映射流形约束”的核心工具，本质是一种 快速将任意非负矩阵转换成“双随机矩阵”的迭代算法——简单说，就是给矩阵加“规矩”（行和、列和都等于1，元素非负）的“标准化工具”，完全适配 mHC 对残差映射的约束需求。

一、先明确核心目标：什么是“双随机矩阵”？

算法的最终输出必须满足 3 个条件（和 mHC 的约束要求完全对齐）：

1. 所有元素都是非负数（≥0）；
2. 每行的元素加起来等于 1（行和=1）；
3. 每列的元素加起来等于 1（列和=1）。

举个例子（n=4，对应 4 条残差流）：
符合要求的双随机矩阵（行和、列和都=1）：

[0.2, 0.3, 0.4, 0.1]  # 行和=1
[0.3, 0.2, 0.2, 0.3]  # 行和=1
[0.2, 0.3, 0.1, 0.4]  # 行和=1
[0.3, 0.2, 0.3, 0.2]  # 行和=1
列和：1.0  1.0  1.0  1.0  # 每列加起来也=1

而 mHC 中未经约束的原始残差映射 \(\tilde{\mathcal{H}}_{l}^{res}\) 可能是“杂乱无章”的（比如行和=3.2、列和=0.5，元素有正有负），Sinkhorn-Knopp 算法就是把这种“乱矩阵”改成上面的“规矩矩阵”。

二、算法核心步骤：3 步迭代，简单粗暴

算法的逻辑特别直观，就像“反复调整行和列的比例”，直到满足要求，全程只有 3 个核心步骤（迭代执行）：

前提：先把矩阵“转正”

输入的原始残差映射 \(\tilde{\mathcal{H}}_{l}^{res}\) 可能有负数（会导致信息抵消），所以第一步先做“指数操作”：
\(M^{(0)} = \exp(\tilde{\mathcal{H}}_{l}^{res})\)

• \(\exp(\cdot)\) 是指数函数（e 的 x 次方），不管输入是正还是负，输出都是正数（≥0）；
• 这一步直接满足“元素非负”的约束，同时保留原始映射的信息分布（不会打乱通道混合的大致趋势）。

迭代：交替归一化行和列（核心操作）

从 \(M^{(0)}\) 开始，反复执行“行归一化→列归一化”，直到行和、列和都接近 1（迭代次数足够时收敛）：

1. 列归一化（\(T_c\)）：把矩阵每一列的所有元素，都除以这一列的总和，让每列的和变成 1；
2. 行归一化（\(T_r\)）：把经过列归一化的矩阵，再对每一行做同样操作，让每行的和变成 1；
3. 重复第 1-2 步，直到行和、列和都稳定在 1 左右（论文中选了 20 次迭代，兼顾效果和速度）。

输出：得到双随机矩阵

迭代停止后，最终的矩阵 \(M^{(t_{max})}\) 就是满足约束的残差映射 \(\mathcal{H}_{l}^{res}\)，可以直接用到 mHC 的核心传播公式中。

三、通俗类比：给矩阵做“比例校准”

把残差映射矩阵想象成“n 条输入通道向 n 条输出通道分配信息的比例表”：

• 原始矩阵（\(\tilde{\mathcal{H}}_{l}^{res}\)）：分配比例混乱（比如输入通道 1 给输出通道 1 分配 5.2，给输出通道 2 分配 -0.3，总和也不等于 1）；
• 指数操作：先把所有分配比例改成正数（比如 -0.3 变成 \(\exp(-0.3)≈0.74\)），避免“负向抵消”；
• 交替归一化：就像“调整天平”——先让每列的总比例=1（保证每条输出通道收到的总信息不超标），再让每行的总比例=1（保证每条输入通道的信息全部分配完，不浪费），反复调几次，比例就完全均衡了。

四、为什么 mHC 非要用这个算法？

1. 适配性强：刚好能产出 mHC 需要的“双随机矩阵”，完美解决 HC 残差映射无约束的问题；
2. 计算高效：迭代次数少（论文只用 20 次），不会给模型增加太多计算负担（mHC 整体额外开销仅 6.7%）；
3. 保信息：只是调整“分配比例”，不会改变原始映射的核心信息（比如哪条通道的信息更重要），兼顾稳定性和模型表达能力。

总结

Sinkhorn-Knopp 算法就是 mHC 的“规则执行者”——它把原本“随心所欲”的残差映射矩阵，通过“转正→交替归一化”的简单迭代，变成“行和列和都=1、元素非负”的双随机矩阵，从而给残差流的信息传递加了“流量控制器”，避免信息爆炸或消失，让大模型能稳定规模化训练。