匀速贝塞尔曲线运动

就是沿着贝塞尔曲线匀速运动，相同时间走相同的曲线距离。

 

贝塞尔曲线公式

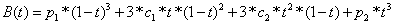，其中p₁为起点，p₂为终点，c₁为控制点1，c₂为控制点2，变量t的范围为[0, 1]。

注意：这边的变量用t不是时间

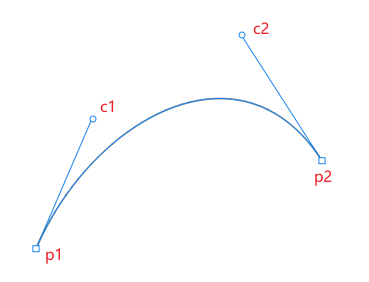
public static Vector3 GetBezierPoint(Vector3 p1, Vector3 c1, Vector3 c2, Vector3 p2, float t)
{
    float rest = (1f - t);
    // p1*(1-t)^3 + 3*c1*t*(1-t)^2 + 3 *c2*t^2*(1-t) * p2*t^3
    Vector3 result = p1 * rest * rest * rest + 3 * c1 * t * rest * rest + 3f * c2 * t * t * rest + p2 * t * t * t;
    return result;
}

 

上面公式的得到贝塞尔曲线上的一个点，那能计算出从p1以速度v=10沿着曲线运动1s后的点坐标么？

显然不能，这边还缺一个根据曲线长度计算出t的公式。有了t，只要代入函数B(t)就能算出点坐标了

 

根据曲线长度计算t的推导

1) 求出曲线长度公式

  1-a) 先把贝塞尔曲线公式展开成A*t³ + B*t² + C*t + D的形式 

    

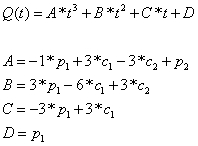
public static void BezierExpand(Vector3 p1, Vector3 c1, Vector3 c2, Vector3 p2, out Vector3 A, out Vector3 B, out Vector3 C, out Vector3 D)
{
    A = -1 * p1 + 3 * c1 - 3 * c2 + p2;
    B = 3 * p1 - 6 * c1 + 3 * c2;
    C = -3 * p1 + 3 * c1;
    D = p1;
}

 

  1-b) 对函数Q(t)求导，得到的导函数Q'(t)可以用于求Q(t)在t处的变化率。（不知道怎么求导的，找关键字：幂函数求导或常见函数求导）

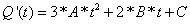    ，导数Q'(t)的结果是一个向量（即两个点相减） 

 

  1-c) 利用微积分思想得到曲线长度公式

    就是将曲线切分成超级多份，这样每一份就非常的小，可以近似的当做线段处理，然后把这些线段的长度相加，就是曲线长度。而导数做的就是计算每一份的大小，所以曲线长度公式：

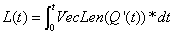    ，因为Q'(x)的结果是一个向量，VecLen表示求向量的长度。

 

  1-d) L(t)是一个积分公式，求积分的方法很多，有：基本积分法，换元积分法，分部积分法，数值积分法等。

    这边的话使用数值积分法中的Gauss-Legendre求积公式来求积分：

    

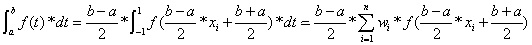
    其中n表示积分点数量，n与w_i, x_i的取值可以通过查表获得，都是预计算好的（Gaussian Quadrature Weights and Abscissae），n取得越大精度越高，但计算量也相应变大，这边的话用10；

    a对应变量t的下限0，b对应变量t；f(t)对应VecLen(Q'(x))，所以最终曲线长度公式：

    

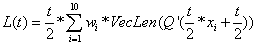
// 曲线公式一阶导数, 对应Q'(t)
public Vector3 GetPointDer(float t)
{
    return 3f * A * t * t + 2f * B * t + C;
}

// 获取曲线长度, 对应L(t)
public float GetArcLength(float t)
{
    var halfT = t / 2f;

    float sum = 0f;
    foreach (var wx in gaussWX)
    {
        var w_i = wx[0];
        var x_i = wx[1];
        sum += w_i * GetPointDer(halfT * x_i + halfT).magnitude;
    }
    sum *= halfT;
    return sum;
}

 

2) 根据曲线长度，求贝塞尔曲线公式的变量t的值

  比如：曲线长度为5时，求出t的值，怎么求？

    直接代入上面的公式，然后解出方程即可：

   

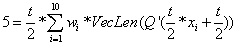
  但是会发现上面的方程还挺复杂的，还又有累加，又有导数的，解这种复杂的方程，可以使用牛顿迭代法，公式为：

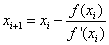    ，其中x_i+1表示本次迭代后的值，x_i表示上次迭代的值，f(x)对应：L(t)-曲线长度

//用[0, 1]方式表示的曲线长度
public float T2NormalS(float t)
{
    return GetArcLength(t) / arcLength;
}

//曲线长度函数导数/曲线长度
public float T2NormalSDer(float t)
{
    return GetPointDer(t).magnitude / arcLength;
}

//根据曲线长度获取贝塞尔曲线公式的变量t
public float S2T(float normalS)
{
    const int NEWTON_SEGMENT = 4; //迭代次数

    normalS = Mathf.Clamp01(normalS);
    float t = normalS;
    for (int i = 0; i < NEWTON_SEGMENT; i++)
    {
        t = t - (T2NormalS(t) - normalS) / T2NormalSDer(t);
    }
    return t;
}

//根据距离获取贝塞尔曲线上的点
public Vector3 GetPointByNormalS(float normalS)
{
    float t = S2T(normalS);
    return GetPoint(t);
}

 

其他

//获取曲线的切线
public static Vector3 GetBezierTangent(Vector3 p1, Vector3 c1, Vector3 c2, Vector3 p2, float t)
{
    float rest = 1 - t;
    float sqr_t = t * t;
    float sqr_rest = rest * rest;

    // 3*A*t^2 + 2*B*t + C
    //A, B, C代入后:
    // 3*t^2*(-p1 + 3*c1 - 3*c2 + p2) = 3*t^2*p1 + -9*t^2*c1 + 9*t^2*c2 - 3*t^2*p2
    // 2*t*(3*p1 - 6*c1 + 3*c2) = 6*t*p1 - 12*t*c1 + 6*t*c2
    // -3*p1 + 3*c1
    //合并下:
    // (-3*t^2 + 6*t - 3)*p1 = -3*(t^2 -2*t + 1)*p1 = -3*(t-1)^2*p1
    // (9*t^2 - 12*t + 3)*c1 = 3*(3*t^2 - 4*t + 1)*c1 = 3*((1-t)^2 - 2*t*(1-t))*c1
    // (-9*t^2 + 6*t)*c2 = 3*(-3*t^2 + 2*t)*c2 = 3*(2*t*(1-t) - t^2)*c2
    // 3*t^2*p2

    Vector3 p = p1 * -3 * sqr_rest;
    p = p + c1 * 3 * (sqr_rest - 2 * t * rest);
    p = p + c2 * 3 * (2 * t * rest - sqr_t);
    p = p + p2 * 3 * sqr_t;

    return p; //p.GetNormalized();
}

 

参考

Unity3D 参数曲线 实现曲线上的匀速运动 - 知乎

牛顿迭代法（Newton's method） - 知乎

牛顿迭代法求解一元高阶方程_一元高次方程解法-CSDN博客

轻松理解牛顿迭代法且用其求平方根_newton 迭代法 求平方根-CSDN博客

方程的根和解的区别，方程：含有未知数的等式。使等式成立的未知数的值称为“解”或“根”

泰勒展开式（常见）_泰勒公式常用展开式-CSDN博客