Vector3常用方法

向量普通乘

(x1, y1, z1)*(x2, y2, z2)=(x1*x2, y1*y2, z1*z2)

普通乘这个式子就是让分量相乘，没有为啥是这么算。shader中的Blend的颜色乘 DstColor*SrcColor + Zero*DstColor也是类似

 

Vector3.Dot(v1, v2)

a) 向量点乘 v1●v2

b1) 计算公式1: 

b2) 计算公式2:

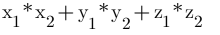
c) 用途:

c1) 计算v1在v2上的投影长度(v2为单位向量时)；计算v2在v1上的投影长度(v1为单位向量时)。

比如：角色在相机观看方向上的距离 Vector3.Dot(playerPos, cameraForwardDir)

c2) 可以通过上面的公式, 计算向量夹角cos值

c3) 要求的值，与向量夹角的cos值成正比时，就可以考虑用单位向量的点乘来算。比如： 光照中，漫反射光线强度与表面法线和光源方向的夹角的cos值成正比（夹角越大，漫反射强度越弱）

 

Vector3.Angle(v1, v2)

a) 求两个向量的夹角, 范围为[0, 180]（ 反余弦函数(arccos)的结果范围[0, 180]）

b) 可以从点乘公式得出

 

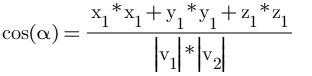
示例1：v1(0, 0, 4), v2(3, 0, -3), 两个向量的角度为135度

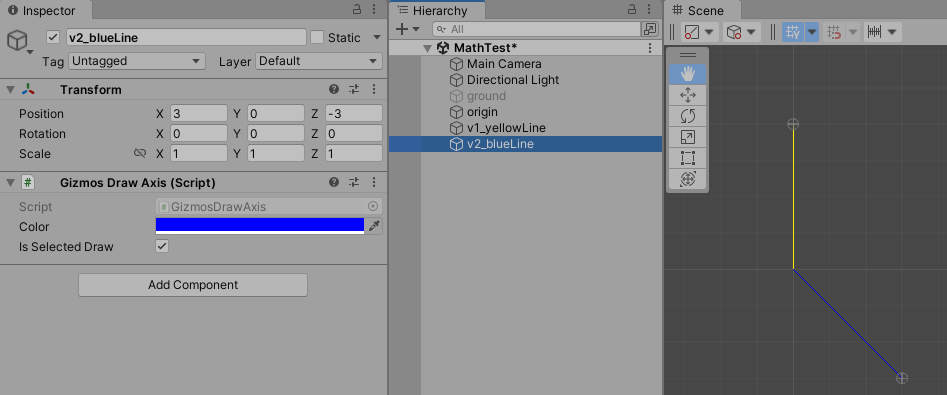
示例2：v1(0, 0, 4), v2(3, 0, -3), 两个向量的角度为135度

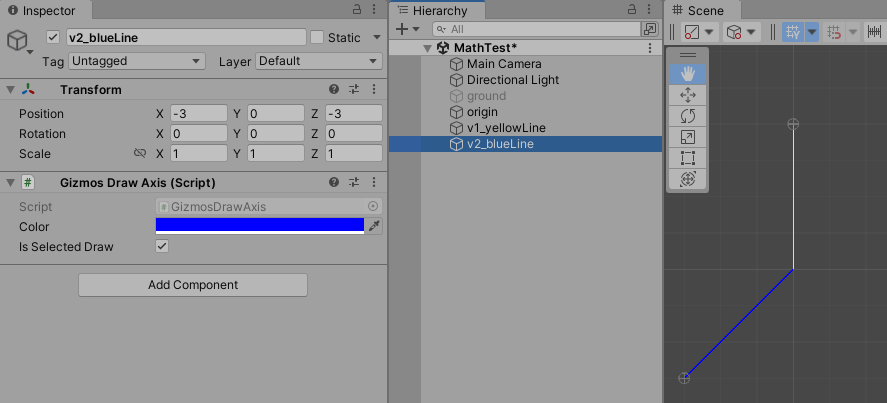
c) Vector3.Angle不会超过180度，也不会为负值

var v1 = new Vector3(1, 0, 0);

var v2 = new Vector3(-1, 1, 0);

Debug.Log($"{Vector3.Angle(v1, v2)}"); //135度

 

var v3 = new Vector3(-1, -1, 0);

Debug.Log($"{Vector3.Angle(v1, v3)}"); //135度

 

var v4 = new Vector3(1, -1, 0);

Debug.Log($"{Vector3.Angle(v1, v4)}"); //45度

 

Vector3.Cross(v1, v2)

a) 向量叉乘 v1×v2

b) 用途: 可以得到一个垂直于向量v1, v2的向量v3; 然后又可以对v1, v3做叉乘, 得到一个垂直于v1, v3的向量v4（v1, v3, v4相互垂直，就类似x轴，y轴，z轴那样了）

c) 公式: (y1*z2 - z1*y2, x2*z1 - x1*z2, x1*y2 - y1*x2)

d) z轴为0时(二维向量)的公式:  (0, 0, x1*y2 - y1*x2)或 (0, 0, |v1|*|v2|*sin_a)。

注意：有的教程中，二维向量的教程直接写成了: v1×v2 = x1*y2 - y1*x2 = |v1|*|v2|*sin_a, 这样很容易造成误导，认为叉乘的结构是一个值(标量)，这是不对的。

e) 如果是2维向量，可以用于判断向量是否平行或共线(此时叉乘结果为0)。

f) 如果是2维向量：

f-1) 叉乘结果>0，v1逆时针旋转到v2的角度在180度内，因为sin在(0, 180)区间结果>0

f-2) 叉乘结果<0，v1顺时针旋转到v2的角度在180度内，因为sin在(180, 360)区间结果<0

f-3) 叉乘结果=0，v1和v2的角度为0度或180度，sin(0)和sin(180)结果均为0，即：两向量平行或共线

v1(0, 0, 4), v2(3, 0, -3), 叉乘得到的向量v3是红色那根线

using UnityEngine;

public class MathTest : MonoBehaviour
{

    public Transform tf1;
    public Transform tf2;

    void Update()
    {
        if (Input.GetKey(KeyCode.Alpha1))
        {
            var v1 = tf1.position;
            var v2 = tf2.position;
            Debug.DrawLine(v1, Vector3.zero, Color.blue);
            Debug.DrawLine(v2, Vector3.zero, Color.yellow);

            var v3 = Vector3.Cross(v1, v2);
            Debug.DrawLine(v3, Vector3.zero, Color.red);
        }
    }
}

 

Vector3.Magnitude

a) 向量长度, 即|v1|=根号(x1*x1 + y1*y1 + z1*z1)

 

Vectro3.SqrMagnitude

a) 向量长度的平方, 即|v1|=x1*x1 + y1*y1 + z1*z1

b) 用途, 减少一次开根号的运算, 对于运算量大的情况, 通过不开根号做相关运算可以在一定程度上优化性能

 

Vector3.Distance(v1, v2)

a) 两个向量的距离，公式: 根号(sqrt(x1-x2) + sqrt(y1-y2) + sqrt(z1-z2))

using UnityEngine;

public class MathTest : MonoBehaviour
{

    public Transform tf1;
    public Transform tf2;

    void Update()
    {
        if (Input.GetKey(KeyCode.Alpha1))
        {
            var v1 = tf1.position;
            var v2 = tf2.position;
            Debug.DrawLine(v1, Vector3.zero, Color.blue);
            Debug.DrawLine(v2, Vector3.zero, Color.yellow);

            var dis = Vector3.Distance(v1, v2);
            Debug.DrawLine(v1, v2, Color.red);
        }
    }
}

 

Vector3.Normalize

a) 求单位向量

 

 

Vector3.Lerp(v1, v2, t)

a) 线性插值。对于位置用这个插值函数

Vectro3.Slerp(v1, v2, t)

b) 球形插值。对于角度或转向这种操作, 用这个插值函数

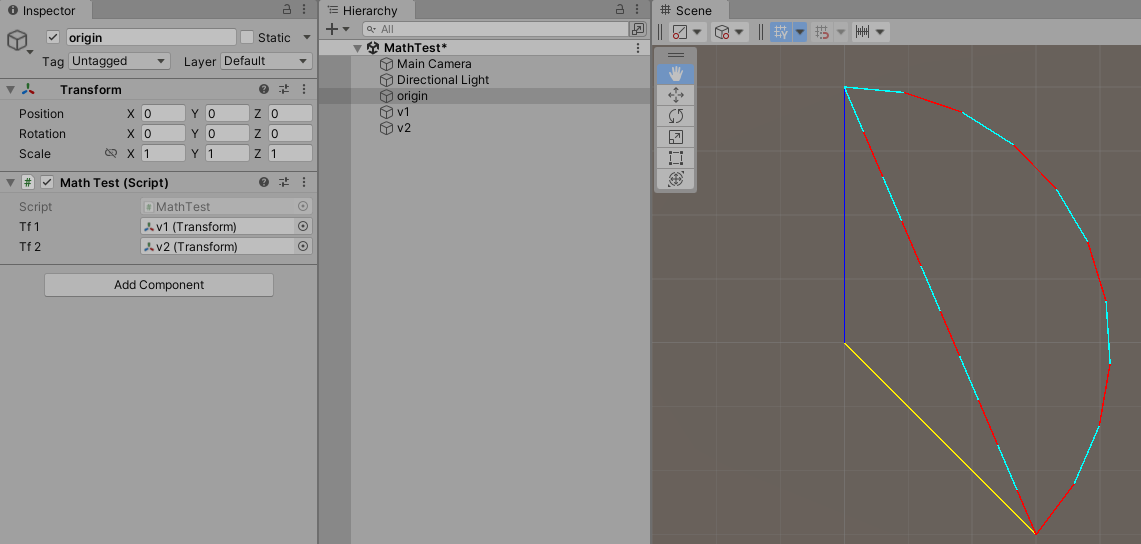
using UnityEngine;

public class MathTest : MonoBehaviour
{

    public Transform tf1;
    public Transform tf2;

    void Update()
    {
        if (Input.GetKey(KeyCode.Alpha1))
        {
            var v1 = tf1.position;
            var v2 = tf2.position;
            Debug.DrawLine(v1, Vector3.zero, Color.blue);
            Debug.DrawLine(v2, Vector3.zero, Color.yellow);

            var lastPos = v1;
            for (var i = 1; i <= 10; ++i)
            {
                var v3 = Vector3.Lerp(v1, v2, 0.1f * i);
                if (i % 2 == 0)
                    Debug.DrawLine(v3, lastPos, Color.red);
                else
                    Debug.DrawLine(v3, lastPos, Color.cyan);
                lastPos = v3;
            }

            lastPos = v1;
            for (var i = 1; i <= 10; ++i)
            {
                var v3 = Vector3.Slerp(v1, v2, 0.1f * i);
                if (i % 2 == 0)
                    Debug.DrawLine(v3, lastPos, Color.red);
                else
                    Debug.DrawLine(v3, lastPos, Color.cyan);
                lastPos = v3;
            }

        }
    }
}

 

关于基向量i, j, k

一般就是对应x, y, z轴的3个基向量，i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1)

所以看到这样的写法要认识：(a, b, c) = ai + bj + ck, 其中a, b, c为常数