【机器学习】信息熵、条件熵、相对熵、交叉熵

信息熵：由信息量的概念引出信息熵，首先要知道信息量的公式的由来(4点推导出)，某个事件的信息量就是 这个事件发生的负对数。而信息熵是跟所有可能性有关系的。每个可能事件的发生都有个概率。信息熵就是平均而言，发生一个时间我们可以得到的信息量的大小。所以从数学上看，信息熵其实是信息量的期望（公式详见正文）。

条件熵：

相对熵：

交叉熵

 

 

 

1、信息熵

信息是不是可以量化？起码直觉上而言是可以的，不然怎么可能我们觉得有些人说的废话特别多，“没什么信息量”，有些人一语中的，一句话就传达了很大的信息量。

为什么有的信息量大有的信息量小？有些事情本来不是很确定，例如明天股票是涨还是跌。如果你告诉我明天NBA决赛开始了，这两者似乎没啥关系啊，所以你的信息对明天股票是涨是跌带来的信息量很少。但是假如NBA决赛一开始，大家都不关注股票了没人坐庄股票有99%的概率会跌，那你这句话信息量就很大，因为本来不确定的事情变得十分确定。

而有些事情本来就很确定了，例如太阳从东边升起，你再告诉我一百遍太阳从东边升起，你的话还是丝毫没有信息量的，因为这事情不能更确定了。

所以说信息量的大小跟事情不确定性的变化有关。

那么，不确定性的变化跟什么有关呢？
一，跟事情的可能结果的数量有关；二，跟概率有关。
先说一。
例如我们讨论太阳从哪升起。本来就只有一个结果，我们早就知道，那么无论谁传递任何信息都是没有信息量的。
当可能结果数量比较大时，我们得到的新信息才有潜力拥有大信息量。

二，单看可能结果数量不够，还要看初始的概率分布。例如一开始我就知道小明在电影院的有15*15个座位的A厅看电影。小明可以坐的位置有225个，可能结果数量算多了。可是假如我们一开始就知道小明坐在第一排的最左边的可能是99%，坐其它位置的可能性微乎其微，那么在大多数情况下，你再告诉我小明的什么信息也没有多大用，因为我们几乎确定小明坐第一排的最左边了。

那么，怎么衡量不确定性的变化的大小呢？怎么定义呢？
这个问题不好回答，但是假设我们已经知道这个量已经存在了，不妨就叫做信息量，那么你觉得信息量起码该满足些什么特点呢？

 

（1）起码不是个负数吧，不然说句话还偷走信息呢~

（2）起码信息量和信息量之间可以相加吧！假如你告诉我的第一句话的信息量是3，在第一句话的基础上又告诉我一句话，额外信息量是4，那么两句话信息量加起来应该等于7吧！难道还能是5是9？

（3）刚刚已经提过，信息量跟概率有关系，但我们应该会觉得，信息量是连续依赖于概率的吧！就是说，某一个概率变化了0.0000001，那么这个信息量不应该变化很大。

（4）刚刚也提过，信息量大小跟可能结果数量有关。假如每一个可能的结果出现的概率一样，那么对于可能结果数量多的那个事件，新信息有更大的潜力具有更大的信息量，因为初始状态下不确定性更大。

那有什么函数能满足上面四个条件呢？负的对数函数，也就是-log(x) 底数取大于1的数保证这个函数是非负的就行。前面再随便乘个正常数也行。
a. 为什么不是正的？因为假如是正的，由于x是小于等于1的数，log(x)就小于等于0了。第(1)个特点满足。
b. 咱们再来验证一下其他特点。(3)是最容易的。假如x是一个概率，那么log(x)是连续依赖于x的。done
c. (4)呢？假如有n个可能结果，那么出现任意一个的概率是1/n，而-log(1/n)是n的增函数，没问题。
d。最后验证(4)。由于-log(xy) = -log(x) -log(y)，所以也是对的。学数学的同学注意，这里的y可以是给定x的条件概率，当然也可以独立于x。

By the way，这个函数是唯一的(除了还可以多乘上任意一个常数)，有时间可以自己证明一下，或者查书。

ok，所以我们知道一个事件的信息量就是这个事件发生的概率的负对数。

最后终于能回到信息熵。信息熵是跟所有可能性有关系的。每个可能事件的发生都有个概率。信息熵就是平均而言发生一个事件我们得到的信息量大小。所以数学上，信息熵其实是信息量的期望。即：
                                                                                  

熵最早是由热力学定义的一个函数，是普朗克来中国讲学的时候引入的。英文是“entropy”这个字，中文词汇中没有相关的字眼。当时是一个有名的姓胡的学者作为普朗克的翻译。因为这个熵“S”是定义为热量Q与温度的比值，所以当时他翻译是立刻创造出熵这个字，从火，从商。

 

2、条件熵

条件熵 𝐻(𝑌|𝑋) 表示在已知随机变量 𝑋 的条件下随机变量 𝑌 的不确定性。条件熵 𝐻(𝑌|𝑋) 定义为 𝑋 给定条件下， 𝑌 的条件概率分布的熵对  𝑋 的数学期望：

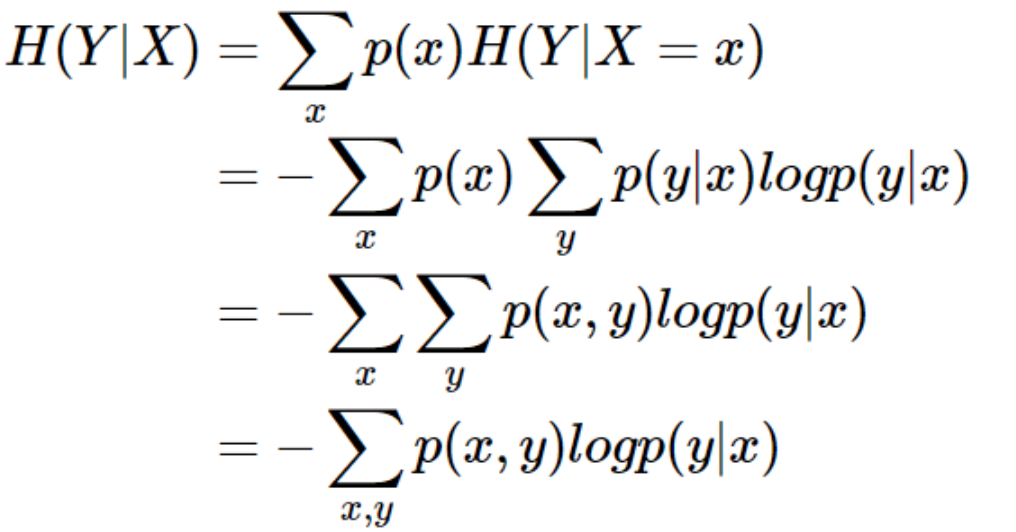
 条件熵 𝐻(𝑌|𝑋) 相当于联合熵 𝐻(𝑋,𝑌) 减去单独的熵 𝐻(𝑋)，即 𝐻(𝑌|𝑋)=𝐻(𝑋,𝑌)−𝐻(𝑋)，证明如下：

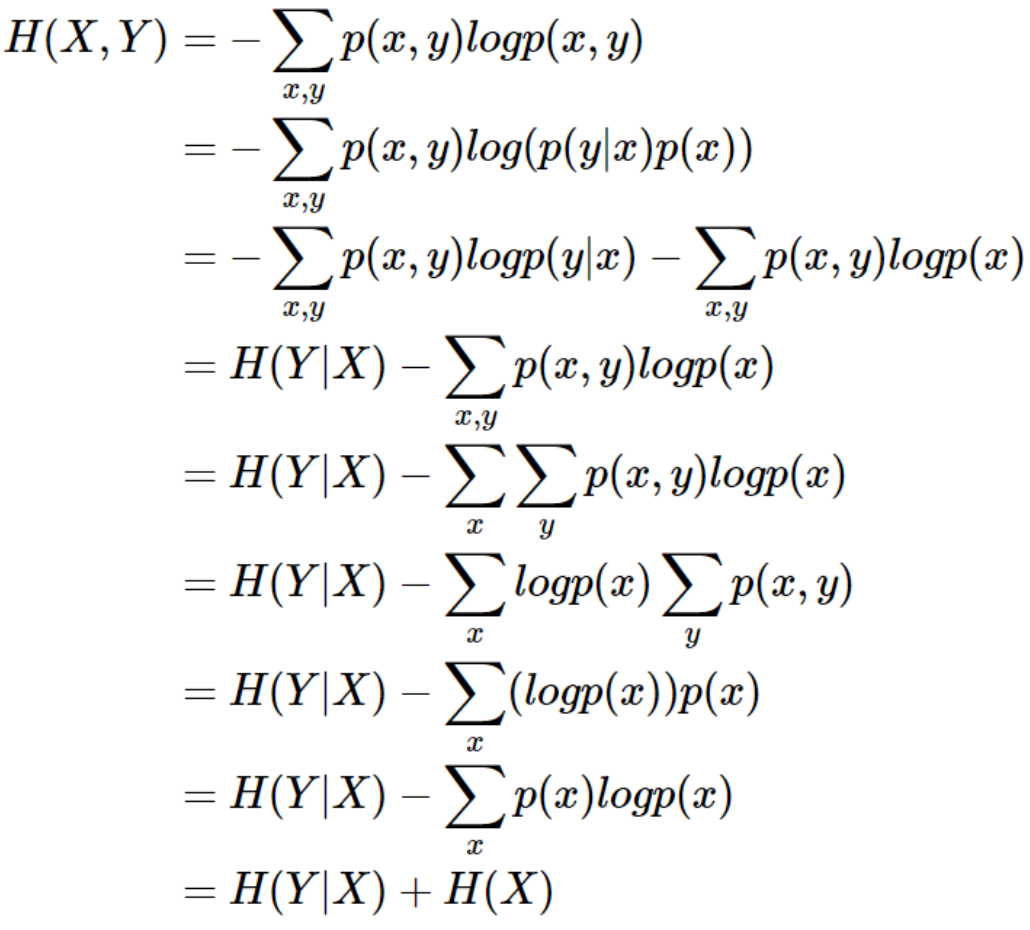
举个例子，比如环境温度是低还是高，和我穿短袖还是外套这两个事件可以组成联合概率分布 𝐻(𝑋,𝑌) ，因为两个事件加起来的信息量肯定是大于单一事件的信息量的。

假设 𝐻(𝑋) 对应着今天环境温度的信息量，由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的，所以在已知今天环境温度的情况下，我穿什么衣服的信息量

或者说不确定性是被减少了。当已知 𝐻(𝑋)这个信息量的时候，𝐻(𝑋,𝑌) 剩下的信息量就是条件熵：

𝐻(𝑌|𝑋)=𝐻(𝑋,𝑌)−𝐻(𝑋)

因此，可以这样理解，描述 𝑋 和 𝑌 所需的信息是描述 𝑋 自己所需的信息,加上给定  𝑋  的条件下具体化  𝑌  所需的额外信息。

 

3、相对熵

Kullback-Leibler Divergence，即K-L散度，是一种量化两种概率分布P和Q之间差异的方式，又叫相对熵。在概率学和统计学上，我们经常会使用一种更简单的、近似的分布来替代观察数据或太复杂的分布。K-L散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息量。

我们从下面这个问题出发思考K-L散度。

假设我们是一群太空科学家，经过遥远的旅行，来到了一颗新发现的星球。在这个星球上，生存着一种长有牙齿的蠕虫，引起了我们的研究兴趣。我们发现这种蠕虫生有10颗牙齿，但是因为不注意口腔卫生，又喜欢嚼东西，许多蠕虫会掉牙。收集大量样本之后，我们得到关于蠕虫牙齿数量的经验分布，如下图所示：

 

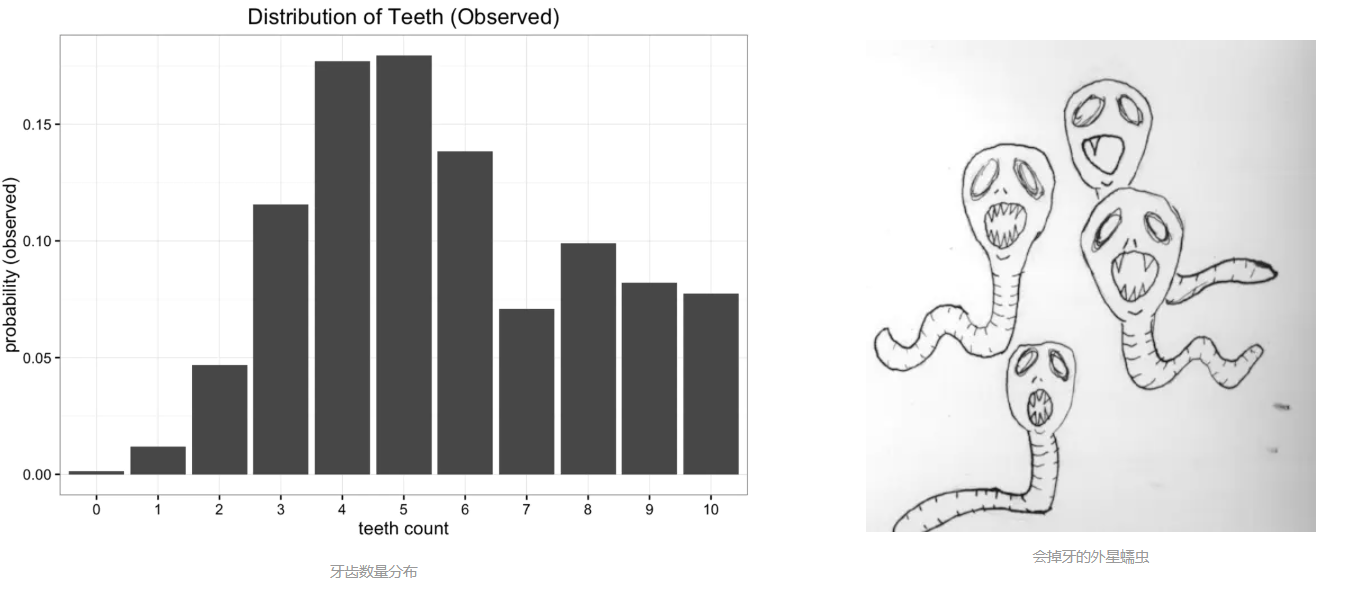
这些数据很有价值，但是也有点问题。我们距离地球🌍太远了，把这些概率分布数据发送回地球过于昂贵。还好我们是一群聪明的科学家，用一个只有一两个参数的简单模型来近似原始数据会减小数据传送量。最简单的近似模型是均分布，因为蠕虫牙齿不会超过10颗，所以有11个可能值，那蠕虫的牙齿数量概率都为 1/11。分布图如下：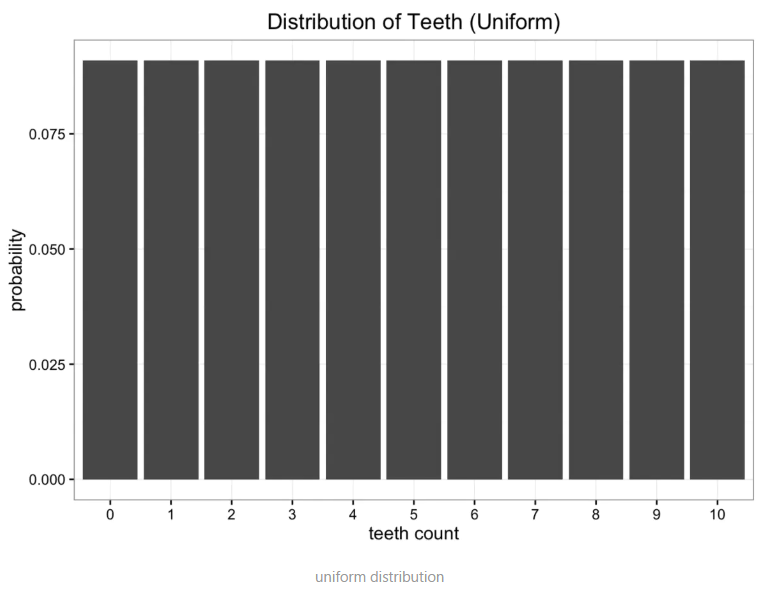

显然我们的原始数据并非均分布的，但也不是我们已知的分布，至少不是常见的分布。作为备选，我们想到的另一种简单模型是二项式分布binomial distribution。蠕虫嘴里面共有n=10个牙槽，每个牙槽出现牙齿与否为独立事件，且概率均为p。则蠕虫牙齿数量即为期望值E[x]=n*p，真实期望值即为观察数据的平均值，比如说5.7，则p=0.57，得到如下图所示的二项式分布：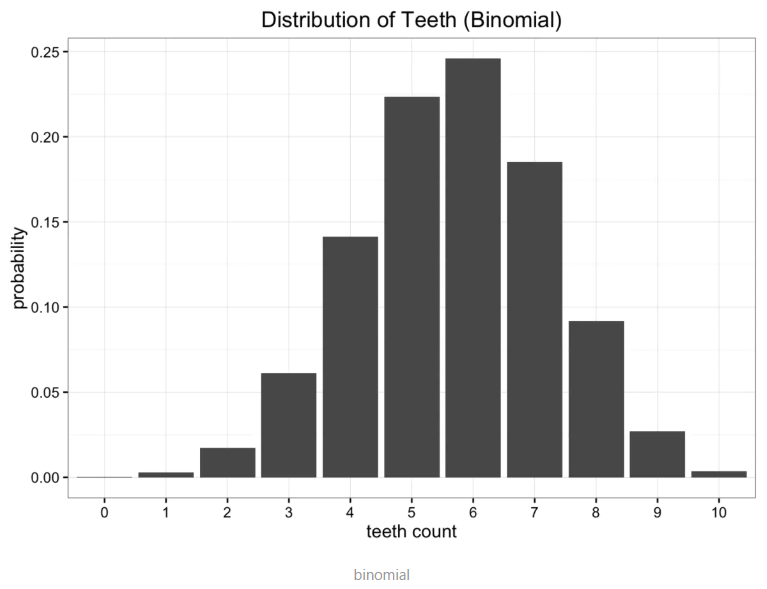

 

对比一下原始数据，可以看出均分布和二项分布都不能完全描述原始分布。

 

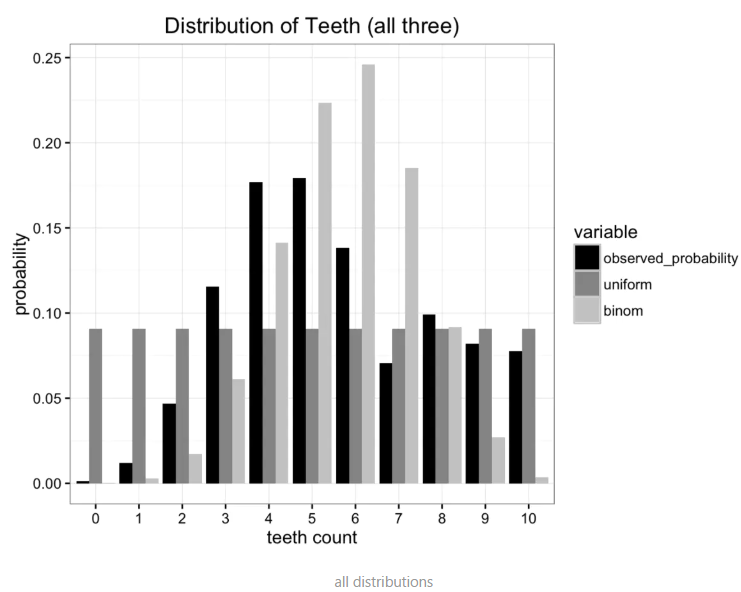
可是，我们不禁要问，哪一种分布更加接近原始分布呢？
已经有许多度量误差的方式存在，但是我们所要考虑的是减小发送的信息量。上面讨论的均分布和二项式分布都把问题规约到只需要两个参数，牙齿数量和概率值（均分布只需要牙齿数量即可）。那么哪个分布保留了更多的原始数据分布的信息呢？这个时候就需要K-L散度登场了。

数据的熵

K-L散度源于信息论。信息论主要研究如何量化数据中的信息。最重要的信息度量单位是熵Entropy，一般用H表示。分布的熵的公式如下：

 

上面对数没有确定底数，可以是2、e或10，等等。如果我们使用以2为底的对数计算H值的话，可以把这个值H 看作是编码信息所需要的最少二进制位个数bits。上面空间蠕虫的例子中，信息指的是根据观察所得的经验分布给出的蠕虫牙齿数量。计算可以得到原始数据概率分布的熵值为3.12 bits。这个值只是告诉我们编码蠕虫牙齿数量概率的信息需要的二进制位bit的位数。

可是熵值并没有给出压缩数据到最小熵值的方法，即如何编码数据才能达到最优（存储空间最优）。优化信息编码是一个非常有意思的主题，但并不是理解K-L散度所必须的。熵的主要作用是告诉我们（1）最优编码信息方案的理论下界（存储空间），以及（2）度量数据的信息量的一种方式。理解了熵，我们就知道有多少信息蕴含在数据之中，现在我们就可以计算当我们用一个带参数的概率分布来近似替代原始数据分布的时候，到底损失了多少信息。请继续看下节内容。↓↓↓

K-L散度度量信息损失

只需要稍加修改熵H的计算公式就能得到K-L散度的计算公式。设p为观察得到的概率分布，q为另一分布来近似p，则p、q的K-L散度为：

 

显然，根据上面的公式，K-L散度其实是数据的原始分布p和近似分布q之间的对数差值的期望。如果继续用2为底的对数计算，则K-L散度值表示信息损失的二进制位数。下面公式以期望表达K-L散度：

 

一般，K-L散度以下面的书写方式更常见：

 

注：log a - log b = log (a/b)

OK，现在我们知道当用一个分布来近似另一个分布时如何计算信息损失量了。接下来，让我们重新回到最开始的蠕虫牙齿数量概率分布的问题。

对比两种分布

首先是用均分布来近似原始分布的K-L散度：

 

接下来计算用二项式分布近似原始分布的K-L散度：

 

通过上面的计算可以看出，使用均分布近似原始分布的信息损失要比用二项式分布近似小。所以，如果要从均分布和二项式分布中选择一个的话，均分布更好些。

散度并非距离

很自然地，一些同学把K-L散度看作是不同分布之间距离的度量。这是不对的，因为从K-L散度的计算公式就可以看出它不符合对称性（距离度量应该满足对称性）。如果用我们上面观察的数据分布来近似二项式分布，得到如下结果：

 

所以，Dkl (Observed || Binomial) != Dkl (Binomial || Observed)。
也就是说，用p近似q和用q近似p，二者所损失的信息并不是一样的。

使用K-L散度优化模型

前面使用的二项式分布的参数是概率 p=0.57，是原始数据的均值。p的值域在 [0, 1] 之间，我们要选择一个p值，建立二项式分布，目的是最小化近似误差，即K-L散度。那么0.57是最优的吗？
下图是原始数据分布和二项式分布的K-L散度变化随二项式分布参数p变化情况：

二项分布K-L值变化曲线

通过上面的曲线图可以看出，K-L散度值在圆点处最小，即p=0.57。所以我们之前的二项式分布模型已经是最优的二项式模型了。注意，我已经说了，是而像是模型，这里只限定在二项式模型范围内。

前面只考虑了均分布模型和二项式分布模型，接下来我们考虑另外一种模型来近似原始数据。首先把原始数据分成两部分，1）0-5颗牙齿的概率和 2）6-10颗牙齿的概率。概率值如下：

 

 

即，一只蠕虫的牙齿数量x=i的概率为p/5; x=j的概率为(1-p) / 6，i=0,1,2,3,4,5; j=6,7,8,9,10。
Aha，我们自己建立了一个新的（奇怪的）模型来近似原始的分布，模型只有一个参数p，像前面那样优化二项式分布的时候所做的一样，让我们画出K-L散度值随p变化的情况：

当p=0.47时，K-L值取最小值0.338。似曾相识吗？对，这个值和使用均分布的K-L散度值是一样的（这并不能说明什么）！下面我们继续画出这个奇怪模型的概率分布图，看起来确实和均分布的概率分布图相似：

我们自己都说了，这是个奇怪的模型，在K-L值相同的情况下，更倾向于使用更常见的、更简单的均分布模型。

回头看，我们在这一小节中使用K-L散度作为目标方程，分别找到了二项式分布模型的参数p=0.57和上面这个随手建立的模型的参数p=0.47。是的，这就是本节的重点：使用K-L散度作为目标方程来优化模型。当然，本节中的模型都只有一个参数，也可以拓展到有更多参数的高维模型中。

 

 4、交叉熵(Cross entropy)