双指针
双指针算法并不是一个具体的、单一的算法吗，而是一种算法思想和技巧。它通过在数据结构上维护两个指针，并让它们按照一定的规则进行移动，从而在一次遍历中解决问题。
核心目标：双指针的主要目标是优化时间复杂度。通过巧妙地移动两个指针，它能将许多问题中朴素解法的复杂度降低到 \(O(n)\)。它通过减少不必要的、重复的计算来实现这一点。
双指针主要有三种常见的应用模式，理解了这三种模式，就能掌握其精髓。
模式一：对撞指针
这是最经典的一种模式，通常用于已排序的数组。
- 指针设置：一个指针
left指向数组的开头，另一个指针right指向数组的末尾。 - 移动规则：两个指针根据特定条件，相向移动（
left向右，right向左），直到它们相遇或交错。 - 典型应用：在有序数组中查找满足特定条件的两个数。
问题：给定一个已按升序排列的整数数组 numbers，从中找出两个数满足相加之和等于目标数 target。
pair<int, int> twoSumSorted(const vector<int> &numbers, int target) {
if (numbers.size() < 2) return {-1, -1};
// 1. 初始化对撞指针
int left = 0, right = numbers.size() - 1;
// 2. 指针相向移动，直到相遇
while (left < right) {
int sum = numbers[left] + numbers[right];
if (sum == target) {
// 找到了，返回结果
return {left, right};
} else if (sum < target) {
// 和太小，说明左边的数太小了，需要增大，所以 left 右移
left++;
} else { // sum > target
// 和太大，说明右边的数太大了，需要减小，所以 right 左移
right--;
}
}
return {-1, -1}; // 没有找到
}
模式二：快慢指针
这种模式通常用于链表结构中。
- 指针设置：两个指针
slow和fast都从链表的头开始。 - 移动规则：
slow指针每次移动一步，fast指针每次移动两步。 - 典型应用：
- 判断链表是否有环：如果有环，
fast指针最终会从后面“追上”slow指针。 - 寻找链表的中点：当
fast指针到达链表末尾时，slow指针正好位于中点。
- 判断链表是否有环：如果有环，
模式三：滑动窗口
这种模式通常用于寻找数组或字符串中满足特定条件的连续子区间。
- 指针设置：两个指针
left和right都从起点开始，它们共同形成一个“窗口”[left, right]。 - 移动规则：
right指针不断向右移动，以扩大窗口。- 当窗口内的元素满足（或不再满足）某个条件时，
left指针向右移动，以收缩窗口。 - 在整个过程中，记录并更新最优解。
- 典型应用：寻找和为定值的最短子数组、无重复字符的最长子串等。
问题：给定一个含有 n 个正整数的数组 nums 和一个正整数 target。找出该数组中满足其和 >= target 的长度最小的连续子数组。
int minSubArrayLen(int target, vector<int> &nums) {
if (nums.empty()) return 0;
// 1. 初始化滑动窗口指针和辅助变量
int left = 0, currentSum = 0;
int minLength = 0; // 用 0 表示暂时还未找到
// 2. right 指针遍历数组，扩大窗口
for (int right = 0; right < nums.size(); right++) {
currentSum += nums[right];
// 3. 当窗口内的和满足条件时，收缩窗口
while (currentSum >= target) {
// 更新最小长度
if (minLength == 0) minLength = right - left + 1;
else minLength = min(minLength, right - left + 1);
// 收缩窗口：将 left 指针处的元素移出窗口，并移动 left
currentSum -= nums[left];
left++;
}
}
// 如果 minLength 没有被更新过，说明没有找到满足条件的子数组
return minLength;
}
习题：P1102 A-B 数对
解题思路
可以将等式 \(A-B=C\) 变形为 \(B=A-C\)。这样，问题就转化成了：对于数列中的每一个数 \(A\)，去寻找有多少个等于 \(A-C\) 的数 \(B\)。将对每一个 \(A\) 找到的 \(B\) 的数量累加起来，就是最终的答案。
核心算法：排序 + 双指针，为了高效地查找，首先应该对整个数列进行排序。排序是这个解法的关键，它带来了好处，让所有相同的数字都聚集在一起，方便一次性统计它们的数量。
维护两个指针：left 和 right。
- 遍历排序后的数组，对于当前的数
a[i]，把它看作 \(A\)，计算出目标值b = a[i] - c。 - 接下来，移动
left和right指针来找到数组中等于b的数字区间：while (left < n && a[left] < b) left++;这个循环会移动left指针，直到它指向第一个大于或等于b的元素。while (right < n && a[right] <= b) right++;这个循环会移动right指针，直到它指向第一个严格大于b的元素。
- 经过这两步，所有在
[left, right)区间内的元素（即从a[left]到a[right-1]）就是数组中所有等于b的数。这个区间的长度right - left就是b的数量。 - 将这个答案累加到最终答案中。
这个算法最核心的优化在于，当外层循环的 i 不断增大时，由于数组 a 是排好序的，a[i] 也是递增的。因此，计算出的目标 b = a[i] - c 同样是单调不减的。这意味着，在为下一个 a[i] 寻找目标值时，left 和 right 指针不需要从头开始，只需要从上一次停留的位置继续向后移动即可。整个算法中，外层循环遍历一次数组（\(O(n)\)），left 和 right 指针也各自最多只会完整地遍历一次数组（\(O(n)\)）。因此，查找部分的总时间复杂度是 \(O(n)\)。算法的瓶颈在于初始的排序，所以总时间复杂度为 \(O(n \log n)\)。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
using ll = long long;
int main()
{
int n, c; scanf("%d%d", &n, &c);
vector<int> a(n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
sort(a.begin(), a.end());
int left = 0, right = 0;
ll ans = 0;
for (int i = 1; i < n; i++) {
// A = a[i]
int b = a[i] - c;
while (left < n && a[left] < b) left++;
while (right < n && a[right] <= b) right++;
// a[left] 是第一个 >= b 的元素，a[right] 是第一个 > b 的元素
ans += right - left;
}
printf("%lld\n", ans);
return 0;
}
习题：P1638 逛画展
解题思路
这是一个典型的“滑动窗口”问题，非常适合解决在序列中寻找满足特定条件的最短/最长连续子序列的问题。
- 定义“窗口”：用两个指针 \(i,j\) 来定义一个“窗口”，也就是一个连续的区间 \([i,j-1]\)，\(i\) 是窗口的左边界，\(j\) 是窗口的右边界的下一个位置。
- 维护窗口状态
- \(cnt\) 数组：用来统计当前窗口内，每位画家的画作出现了多少次。例如 \(cnt_5\) 就是编号为 \(5\) 的画家的画在窗口内的数量。
- \(tot\) 变量：用来记录当前窗口内包含了多少位不同的画家。
- 算法流程
- 外层循环（固定左边界 \(i\)）：用一个
for循环，让左指针 \(i\) 从 \(1\) 遍历到 \(n\)。在每一轮循环中，都尝试模拟寻找以 \(i\) 为起点的最短有效区间。 - 内层循环（扩展右边界 \(j\)）
- 在固定了左边界 \(i\) 之后，用一个
while循环不断地将右指针 \(j\) 向右移动，将新的画作 \(a_j\) “装入”窗口。 - 每当装入一幅画 \(a_j\)，就在 \(cnt\) 数组中将其对应的画家计数加一。
- 如果这位画家的计数值从 \(0\) 变成了 \(1\)，说明窗口里多了一位之前没有的画家，就将 \(tot\)（不同画家总数）加一。
- 这个
while循环会一直执行，直到窗口内包含了所有 \(m\) 位画家（即 \(tot\) 等于 \(m\)），或者右指针 \(j\) 已经超出了所有画作的范围。
- 在固定了左边界 \(i\) 之后，用一个
- 更新答案
- 当
while循环结束后，如果 \(tot\) 等于 \(m\)，说明找到了一个从 \(i\) 开始的、包含了所有画家的有效区间 \([i,j-1]\)。 - 此时，检查这个区间长度 \((j-1)-i+1\) 是否比已经记录的最小长度 \(y-x+1\) 更短。
- 如果更短，就更新答案。因为 \(i\) 是从左到右依次递增的，所以第一次找到最短长度时，其起始位置 \(x\) 必然是最小的，符合题目要求。
- 当
- 滑动窗口（收缩左边界 \(i\)）
- 在为当前 \(i\) 找到解并更新答案后，
for循环将进入下一次迭代，\(i\) 会变成 \(i+1\)。 - 在移动 \(i\) 之前，需要将旧的左边界元素 \(a_i\) 从窗口中“移除”。
- 具体操作是：将 \(a_i\) 对应画家的计数 \(cnt_{a_i}\) 减一。
- 如果减一后，这位画家的计数值变成了 \(0\)，说明窗口内不再有这位画家的作品了，就将 \(tot\)（不同画家总数）减一。
- 在为当前 \(i\) 找到解并更新答案后，
- 外层循环（固定左边界 \(i\)）：用一个
这个过程就像一个窗口在画作序列上从左到右滑动。通过不断地扩展右边界和收缩左边界，可以在 \(O(n)\) 的线性时间复杂度内，高效地找到问题的最优解。
参考代码
#include <cstdio>
#include <vector>
using namespace std;
int main()
{
int n, m; scanf("%d%d", &n, &m);
vector<int> a(n + 1), cnt(m + 1);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
int x = 1, y = n, tot = 0, j = 1;
for (int i = 1; i <= n; i++) {
while (j <= n && tot < m) {
cnt[a[j]]++;
if (cnt[a[j]] == 1) tot++;
j++;
}
if (j > n && tot < m) break;
if (j - i < y - x + 1) {
x = i; y = j - 1;
}
cnt[a[i]]--;
if (cnt[a[i]] == 0) tot--;
}
printf("%d %d\n", x, y);
return 0;
}
习题：P3143 [USACO16OPEN] Diamond Collector S
解题思路
一、问题简化与预处理
首先，直接在无序的钻石中找会很困难。一个关键的预处理步骤是对所有钻石按大小进行排序。
排序后，一个重要的性质就出现了：任何一个满足条件的展示柜，其包含的钻石在排序后的数组中必然是一个连续的子数组。
为什么？因为如果一个柜子里有钻石 \(a_i\) 和 \(a_j\)（假设 \(i \lt j\)），那么根据条件，\(a_j - a_i \le K\)。对于任何在它们之间的钻石 \(a_k \ (i \lt k \lt j)\)，必然满足 \(a_i \le a_k \le a_j\)，所以 \(a_k - a_i \le a_j - a_i \le K\)。这意味着，如果首尾钻石满足条件，那么它们之间的所有钻石也都满足条件。
现在问题转化为：在排序后的数组中，找到两个不重叠的连续子数组，每个子数组都满足最大减最小小于等于 \(K\) 的条件，并且它们的总长度最长。
二、预处理思想
直接寻找两个不重叠的子数组仍然很复杂。可以换个思路，固定一个“分割点”，然后看分割点左边能找到的最优子数组和右边能找到的最优子数组。
为了实现这一点，需要预处理两个数组：
- \(pre_i\)：表示在原数组的前缀 \([1 \dots i]\) 中，能够找到的满足条件的最长连续子数组的长度。
- \(suf_i\)：表示在原数组的后缀 \([i \dots n]\) 中，能够找到的满足条件的最长连续子数组的长度。
三、计算 \(pre_i\)（从左到右）
\(pre_i\) 的计算可以通过一次遍历和双指针来完成。
- 遍历 \(i\) 从 \(1\) 到 \(n\)。
- 对于每个 \(i\)，想找到以 \(a_i\) 作为最大值的那个满足条件的连续子数组有多长。
- 用一个左指针 \(p\)，它指向这个数组子数组的起始位置。当 \(i\) 向右移动时，\(p\) 也只会向右移动，不会后退。
- 对于当前的 \(a_i\)，移动 \(p\) 直到 \(a_i - a_p \le K\)。此时，子数组 \([p \dots i]\) 就是以 \(a_i\) 为结尾的最长合法子数组，其长度为 \(i - p + 1\)。
- \(pre_i\) 的值，应该是到目前为止（即在前缀 \([1 \dots i]\) 中）所有找到的合法子数组长度的最大值。所以，\(pre_i = \max (pre_{i-1}, i-p+1)\)。
四、计算 \(suf_i\)（从右到左）
\(suf_i\) 的计算与 \(pre_i\) 完全对称，只是方向相反。
- 遍历 \(i\) 从 \(n\) 到 \(1\)。
- 对于每个 \(i\)，想找到以 \(a_i\) 作为最小值的那个满足条件的连续子数组有多长。
- 用一个右指针 \(p\)，从 \(n\) 开始向左移动。
- 对于当前的 \(a_i\)，移动 \(p\) 直到 \(a_p - a_i \le K\)。此时，子数组 \([i \dots p]\) 就是以 \(a_i\) 为起点的最长合法子数组，其长度为 \(p-i+1\)。
- \(suf_i = \max (suf_{i+1}, p-i+1)\)。
五、合并结果
当有了 \(pre\) 和 \(suf\) 两个数组后，就可以轻松地计算最终答案了。可以遍历所有可能的“分割点”，假设在位置 \(i\) 和 \(i+1\) 之间分割数组。
- 左边的部分是 \([1 \dots i]\)，在这个前缀中，能找到的最优解（最长的合法子数组）的长度已经记录在 \(pre_i\) 中了。
- 右边的部分是 \([i+1 \dots n]\)，在这个后缀中，能找到的最优解的长度已经记录在 \(suf_{i+1}\) 中了。
由于这两个部分不重叠，可以把它们的解加起来。遍历所有可能的分割点 \(i\)，计算 \(pre_i + suf_{i+1}\)，并取其中的最大值，就是最终的答案。
时间复杂度瓶颈在于排序，为 \(O(n \log n)\)，后续的两次双指针遍历和一次合并都是 \(O(n)\)，所以总复杂度是 \(O(n \log n)\)。
参考代码
#include <cstdio>
#include <algorithm>
using std::sort;
using std::max;
const int N = 50005;
int a[N], pre[N], suf[N];
int main()
{
int n, k;
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
sort(a + 1, a + n + 1);
int p = 1;
pre[1] = 1;
for (int i = 2; i <= n; i++) {
while (p < i && a[p] < a[i] - k) p++;
pre[i] = max(pre[i - 1], i - p + 1);
}
p = n; pre[n] = 1;
for (int i = n - 1; i >= 1; i--) {
while (p > i && a[p] > a[i] + k) p--;
suf[i] = max(suf[i + 1], p - i + 1);
}
int ans = 0;
for (int i = 1; i < n; i++) ans = max(ans, pre[i] + suf[i + 1]);
printf("%d\n", ans);
return 0;
}
习题：ARC154B New Place
解题思路
题目要求通过将 \(S\) 的首字符移动到任意位置，将其变为 \(T\)，并求最少操作次数。这个操作可以看作：选择 \(S\) 的一个前缀，然后将这个前缀中的所有字符逐一重新插入到 \(S\) 剩下的后缀中。目标是最小化这个前缀的长度，也就是最小化操作次数。
最小化需要移动的前缀，等价于最大化不需要移动的后缀。不移动的字符，它们之间的相对顺序是保持不变的。例如，如果 S = "abac"，决定不移动后缀 "bac"，那么在最终形成的字符串 \(T\) 中，'b'、'a'、'c' 这三个字符必须以 ...b...a...c... 的顺序出现。换句话说，保留的 \(S\) 的后缀，必须是目标字符串 \(T\) 的一个子序列。
因此，问题就转换成了：寻找 \(S\) 的一个最长后缀，这个后缀同时也是 \(T\) 的一个子系列。假设这个最长后缀是 S[k...N-1]，它的长度是 \(N-k\)。这意味着 \(S\) 的前 \(k\) 个字符 S[0...k-1] 是必须移动的，所以，最少操作次数就是 \(k\)。
如何寻找最长后缀？可以从后往前遍历 \(S\) 和 \(T\)，使用两个指针，\(i\) 指向 \(S\) 的末尾，\(j\) 指向 \(T\) 的末尾，尝试将 \(S\) 的后缀与 \(T\) 的后缀进行匹配。当 \(S_i\) 和 \(T_j\) 相等时，说明为 \(S\) 的后缀找到了一个匹配字符，于是将两个指针都向前移动，继续匹配下一个字符。当 \(S_i\) 和 \(T_j\) 不相等时，说明 \(T_j\) 不能作为 \(S_i\) 的匹配项。但 \(S_i\) 可能与 \(T\) 中更靠前的某个字符匹配，所以只把 \(j\) 向前移动，继续在 \(T\) 中为 \(S_i\) 寻找匹配。一直向前匹配，直到 \(i\) 遍历完 \(S\) 所有希望保留的字符。当 \(S_i\) 在 \(T_{0 \dots j}\) 中找不到匹配时，就意味着后缀 \(S_{i \dots N-1}\) 无法构成 \(T\) 的子序列。此时，能构成的最长子序列就是 \(S_{i+1 \dots N-1}\)，必须移动的字符是 \(S_{0 \dots i}\)，共 \(i+1\) 个。
操作只能重排字符，不能增删字符。所以，如果 \(S\) 和 \(T\) 中各类字符的数量本就不相等，那么无论如何操作 \(S\) 都不可能变成 \(T\)，这种情况需要输出 \(-1\)。
参考代码
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int main()
{
int n;
string s, t;
cin >> n >> s >> t;
// --- 步骤 1: 检查字符计数是否相同 ---
vector<int> cnt_s(26, 0);
for (char ch : s) {
cnt_s[ch - 'a']++;
}
vector<int> cnt_t(26, 0);
for (char ch : t) {
cnt_t[ch - 'a']++;
}
// 如果字符集不同, 则不可能通过重排得到, 输出-1
if (cnt_s != cnt_t) {
cout << "-1\n";
return 0;
}
// --- 步骤 2 & 3: 双指针从后往前寻找最长可匹配后缀 ---
int j = n - 1; // 指向 T 的当前待匹配字符位置
// i 指向 S 的当前待匹配字符位置
for (int i = n - 1; i >= 0; i--) {
// 在 T 中为 s[i] 寻找匹配项。只要 T[j] 不是 s[i], 就不断前移 j
while (j >= 0 && s[i] != t[j]) {
j--;
}
// --- 步骤 4: 判断是否找到匹配 ---
// 如果 j < 0, 说明在 T 的剩余部分中找不到 s[i]。
// 这意味着 S 的后缀 S[i...n-1] 无法构成 T 的子序列。
// 最长的可匹配后缀是 S[i+1...n-1]。
// 因此, 必须移动的前缀是 S[0...i], 长度为 i + 1。
if (j < 0) {
cout << i + 1 << "\n";
return 0;
}
// 找到了匹配 s[i] == t[j], 消耗掉 t[j], 将 j 前移, 准备为 s[i-1] 寻找匹配。
j--;
}
// --- 步骤 5: S == T 的情况 ---
// 如果循环正常结束, 说明 S 的整个字符串 (从 n-1 到 0) 都能在 T 中找到匹配。
// 这意味着 S 是 T 的一个子序列。由于长度和字符集都相同, 所以 S 必须等于 T。
// 操作次数为 0。
cout << 0 << "\n";
return 0;
}
习题：P6465 [传智杯 #2 决赛] 课程安排
解题思路
一个一个地枚举所有子数组再进行判断，时间复杂度为 \(O(n^2)\)，对于 \(n = 5 \times 10^5\) 的数据规模来说太慢了，需要一个更高效的算法。
如果固定子数组的右端点，问题就是动态计算此时有多少个合法的左端点。通过一次从左向右的遍历，考察每一个课程作为“结束课程”的所有可能性，并累加合法的方案数。
为了使一个课程安排（即一个连续子数组）合法，它必须同时满足三个条件：
- 长度限制：课程数量不少于 \(l\) 且至少为 \(2\)。
- 内部合法性：课程安排内部不能有相邻的相同课程。
- 首尾合法性：开始的课程和结束的课程不能是同一门。
可以通过一个滑动窗口机制，将这三个条件的检查融合在线性扫描中。
- 维护一个绝对合法的起点：维护一个动态的左边界，这个边界代表了对于当前考察的右端点而言，任何合法的课程安排都必须至少从这个边界开始。这个边界的作用是保证内部合法性。当扫描过程中遇到一对相邻的相同课程时（\(c_i = c_{i-1}\)），就意味着任何包含这对课程的安排都是不合法的。因此，这个绝对合法的起点必须立即向前推进到当前位置，因为所有之前的起点都失效了。
- 确定候选左端点区间：对于每一个被考察的右端点 \(i\)，结合绝对合法的起点和长度限制，可以确定一个候选左端点的连续区间。
- 左边界由绝对合法的起点决定。
- 右边界由长度限制决定。
- 筛选与计数：在确定了候选左端点区间后，已经满足了前两个条件，现在只需处理首尾合法性。
- 需要从候选区间中，排除掉那些与当前右端点课程 \(c_i\) 相同的左端点。
- 维护一个计数器数组 \(cnt\)，动态地记录候选区间内每种课程的数量。
- 因此，对于右端点 \(i\)，新增的合法方案数就等于 \((候选左端点的总数) - (候选左端点中与 c_i 相同的课程数)\)。
这样整个算法通过一次遍历，维护一个动态变化的候选左端点窗口，实现 \(O(n)\) 的时间复杂度。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 500005;
int c[N], cnt[N];
int main()
{
int t; scanf("%d", &t);
while (t--) {
int n, l; scanf("%d%d", &n, &l);
if (l == 1) l = 2;
for (int i = 1; i <= n; i++) {
scanf("%d", &c[i]); cnt[i] = 0;
}
int j = 1;
LL ans = 0;
for (int i = 1; i <= n; i++) {
if (j <= i - l + 1) {
cnt[c[i - l + 1]]++;
}
if (i > 1 && c[i] == c[i - 1]) {
while (j <= i - l + 1) {
cnt[c[j]]--; j++;
}
j = i;
} else if (j <= i - l + 1) {
// [j, i-l+1] 为候选左端点区间
ans += (i - l + 1) - j + 1 - cnt[c[i]];
}
}
printf("%lld\n", ans);
}
return 0;
}
习题：P6739 [BalticOI 2014] Three Friends (Day1)
解题思路
一、基础分析与约束
首先，分析操作过程，可以立刻得到一个强约束：\(U\) 的长度 \(n\) 必须是奇数。如果是偶数，可以直接输出 NOT IMPOSSIBLE。
如果 \(n\) 是奇数，那么可以推断出原始字符串 \(S\) 的长度 \(m = \lfloor n/2 \rfloor\)。
二、核心思路：假设插入位置
既然知道了 \(S\) 的长度 \(m\)，那么 \(U\) 就是由两个 \(S\) 和一个额外字符构成的。这个额外字符被插入的位置是解题的关键。
这个插入的字符，要么是在 \(T\) 的前半部分（第一个 \(S\)），要么是在后半部分（第二个 \(S\)）。无法直接确定它的位置，所以采用假设并验证的策略。
假设一：插入的字符在前一半
- 假设：\(U\) 的前 \(m+1\) 个字符，是由 \(S\) 和一个插入字符构成的。而 \(U\) 的后 \(m\) 个字符，就是完整的、未经修改的 \(S\)。
- 验证
- 基于这个假设，可以提取出候选的 \(S\)。这个 \(S\) 就是 \(U\) 的后半部分，即从 \(U\) 的第 \(m+2\) 个字符开始，取 \(m\) 个字符。
- 接下来，需要验证这个假设是否成立。即，\(U\) 的前半部分（\(U_{1 \dots m+1}\)）是否真的可以由提取出的 \(S\) 加上一个字符得到。
- 这等价于检查：\(U\) 的前半部分去掉一个字符后，是否能与 \(U\) 的后半部分完全匹配。
- 一个高效的验证方法是：用两个指针，一个指向 \(U\) 的开头，一个指向 \(U\) 的后半部分的开头。同时向后移动，如果遇到不匹配的字符，就跳过 \(U\) 前半部分的那个字符一次，然后继续比较。如果最终能完全匹配，说明这个假设是成立的。
假设二：插入的字符在后一半
- 假设：\(U\) 的前 \(m\) 个字符是完整的 \(S\)，\(U\) 的后 \(m+1\) 个字符，是由 \(S\) 和一个插入字符构成的。
- 验证
- 提取候选的 \(S\)：这次，\(S\) 就是 \(U\) 的前半部分，即 \(U_{1 \dots m}\)。
- 验证：检查 \(U\) 的后半部分（\(U_{m+1 \dots n}\)）去掉一个字符后，是否能与 \(U\) 的前半部分完全匹配，验证方法同上。
三、结果判定
在分别对两种假设进行验证后，会得到两个是否成立的结果。根据这两个值，可以做出最终的判定：
- 如果假设一和假设二都不成立，说明不存在任何合法的 \(S\) 能生成 \(U\)，输出
NOT IMPOSSIBLE。 - 如果只有一个成立，找到了唯一的可能性，因此也找到了唯一的 \(S\)，直接输出对应的 \(S\) 即可。
- 如果假设一成立，\(S\) 是 \(U\) 的后半部分。
- 如果假设二成立，\(S\) 是 \(U\) 的前半部分。
- 如果假设一和假设二都成立，说明存在两种不同的方式来解释 \(U\) 的构成，可能对应两个不同的 \(S\)。
- \(S_1\) 来自假设一（\(U\) 的后半部分），\(S_2\) 来自假设二（\(U\) 的前半部分）。
- 需要判断 \(S_1\) 和 \(S_2\) 是否是同一个字符串。
- 如果 \(S_1 = S_2\)，那么虽然有两种解释方式，但它们都指向了同一个原始字符串 \(S\)。因此解是唯一的，输出这个 \(S\)。
- 如果 \(S_1 \ne S_2\)，说明存在两个不同的 \(S\) 都能生成 \(U\)。此时解不唯一，输出
NOT UNIQUE。
参考代码
#include <cstdio>
const int N = 2000005;
char u[N];
int main()
{
int n; scanf("%d%s", &n, u + 1);
if (n % 2 == 0) {
printf("NOT POSSIBLE\n"); return 0;
}
int m = n / 2;
// 假设插入字符在前面一半
int p = m + 2; bool f1 = false;
for (int i = 1; i <= m + 1; i++) {
if (p <= n && u[i] == u[p]) p++;
}
if (p > n) f1 = true;
// 假设插入字符在后面一半
p = 1; bool f2 = false;
for (int i = m + 1; i <= n; i++) {
if (p <= m && u[i] == u[p]) p++;
}
// 前len个字符和后len个字符是否相等
bool f3 = true;
for (int i = 1; i <= m; i++) {
if (u[i] != u[m + 1 + i]) {
f3 = false; break;
}
}
if (p > m) f2 = true;
if (!f1 && !f2) printf("NOT POSSIBLE\n");
else if (f1 && f2 && !f3) printf("NOT UNIQUE\n");
else {
int ans = f1 ? m + 2 : 1;
for (int i = ans; i < ans + m; i++) printf("%c", u[i]);
printf("\n");
}
return 0;
}
习题：P8858 折线
解题思路
显然 \(1\) 个折点是不可能的，至少需要 \(2\) 个折点，而 \(2\) 个折点对应一种非常简单的情况，用一条水平线或竖直线恰好平分 \(n\) 个点，以竖直平分的情况为例，这等价于问是否存在一条竖直线 \(X = k\)（\(k\) 可以不是整数）能平分点集？
可以从 \(1\) 到 \(n\) 枚举 \(x\) 坐标，如果到 \(x = i\) 时恰好有了 \(n/2\) 个点（这可以通过前缀和预处理计算），那么就可以在 \(i\) 和 \(i+1\) 之间画一条竖直线，实现平分。水平线的情况同理。
任何一种检查成功，答案就是 \(2\)，程序结束。
这种构造方案实际上利用了中位数的思想，基于这个思想，可以发现，存在一种 \(4\) 个折点的保底方案，可以实现任意情况的平分。假设对 \(n\) 个点按 \(x\) 坐标升序排序，\(x\) 相等时按 \(y\) 升序。则必然可以构造出一种穿过第 \(n/2\) 个点和第 \(n/2+1\) 个点的折线平分方案，如图所示。
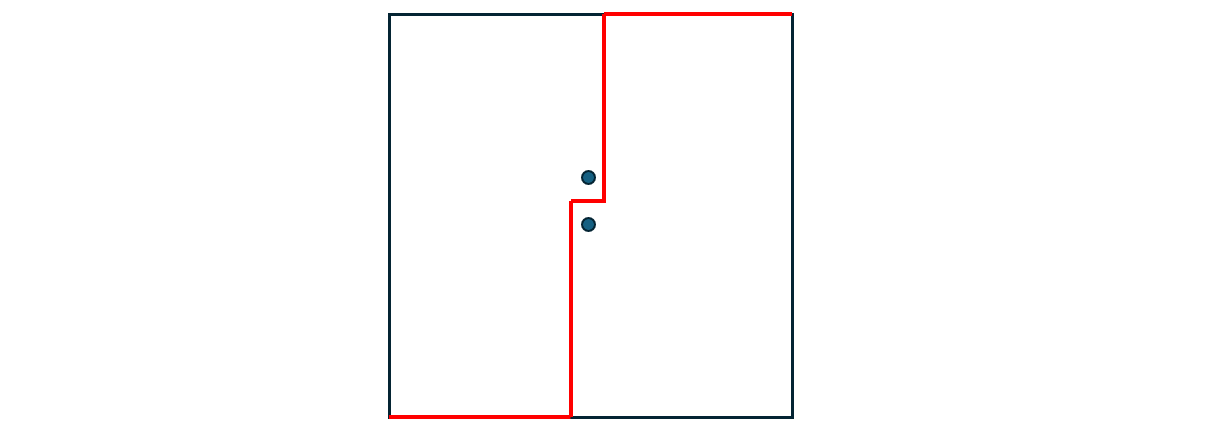
于是问题就转化为了判断是否存在 \(3\) 折点平分方案。而画图可知，三折点平分方案实际上只有两种形状，如图所示：
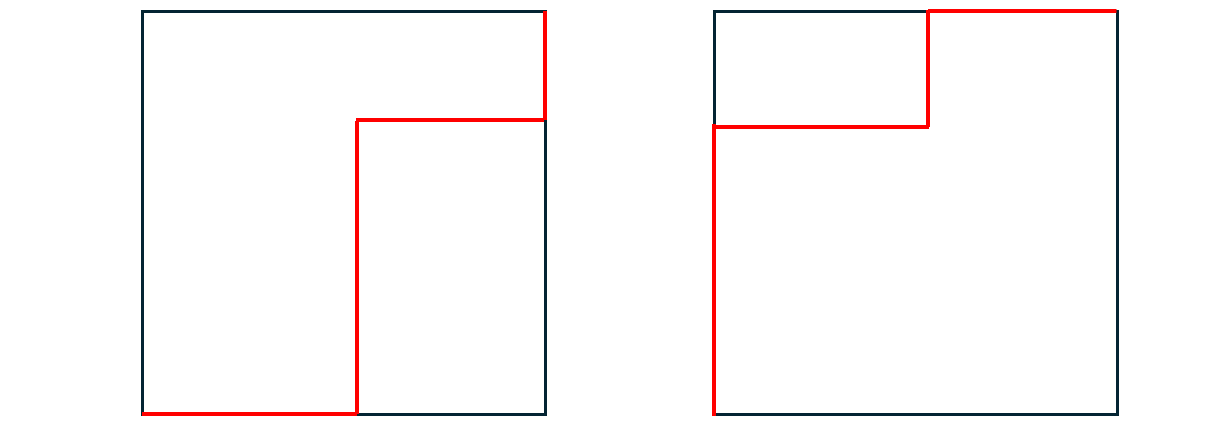
这个问题等价于寻找是否存在一块“左上角”或“右下角”的区域包含恰好 \(n/2\) 个点。
以“右下角”为例分析，假设这块区域最左上角包含的点是 \((x,y)\)，这等于需要快速统计满足 \(x_i \ge x\) 且 \(y_i \le y\) 的点的数量。
让 \(i\) 从 \(n\) 向 \(1\) 扫描，模拟 \(x=i\) 这条竖直线，对于每个 \(i\)，相当于通过找一条水平线 \(y=h\)，使得右下角围起来的点的数量恰好是 \(n/2\)。用一个指针 \(h\) 来寻找这条水平线。随着 \(i\) 的减小，会带来一些新的节点，于是可以下调 \(h\)，使得右下角的点数接近 \(n/2\)。在 \(i\) 的每一轮迭代中，利用双指针调整 \(h\)，检查是否存在某个时刻，使得右下角的点数恰好为 \(n/2\)。
左上角的情况同理。
如何在任何一种检查中得到了解，答案就是 \(3\)，程序结束。
参考代码
#include <cstdio>
#include <vector>
const int N = 500005;
int sumx[N], sumy[N], cnt[N];
std::vector<int> px[N];
void solve() {
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
sumx[i] = sumy[i] = 0;
px[i].clear();
}
for (int i = 1; i <= n; i++) {
int x, y;
scanf("%d%d", &x, &y);
sumx[x]++; sumy[y]++;
px[x].push_back(y);
}
for (int i = 1; i <= n; i++) {
sumx[i] += sumx[i - 1]; sumy[i] += sumy[i - 1];
if (sumx[i] * 2 == n || sumy[i] * 2 == n) {
printf("2\n"); return;
}
}
// 右下角
int tot = 0, h = n;
for (int i = 1; i <= n; i++) cnt[i] = 0;
for (int i = n; i >= 1; i--) {
for (int val : px[i]) {
if (val <= h) {
cnt[val]++; tot++;
}
}
while (h > 0 && tot - cnt[h] >= n / 2) {
tot -= cnt[h]; h--;
}
if (tot * 2 == n) {
printf("3\n"); return;
}
}
// 左上角
tot = 0; h = 1;
for (int i = 1; i <= n; i++) cnt[i] = 0;
for (int i = 1; i <= n; i++) {
for (int val : px[i]) {
if (val >= h) {
cnt[val]++; tot++;
}
}
while (h <= n && tot - cnt[h] >= n / 2) {
tot -= cnt[h]; h++;
}
if (tot * 2 == n) {
printf("3\n"); return;
}
}
printf("4\n");
}
int main()
{
int t; scanf("%d", &t);
for (int i = 1; i <= t; i++) solve();
return 0;
}
习题：CF965D Single-use Stones
解题思路
首先，需要理解限制青蛙数量的关键因素是什么。把河上任意一个连续的、长度为 \(l\) 的区域想象成一个“关卡”或“传送带”，任何一只想要成功过河的青蛙，都必须经过这个区域，并且必须使用该区域内的一块石头作为落脚点。
考虑反证法，假如存在一只青蛙可以过河但避开 \([x-l+1, x]\) 这个区间的石头，那么相当于它至少也从 \(x-l+2\) 位置跳到了 \(x+1\) 位置，这样它的跳跃能力就超出了限制 \(l\)，因此是不可能的。
由于每块石头都是一次性的，一个区域内石头的总数就决定了能通过此“关卡”的青蛙的数量的上限。整个渡河过程是由一系列这样的“关卡”组成的，那么能够成功渡过整条河的青蛙总数，就取决于所有“关卡”中容量最小的那一个。
因此，原问题就转化为了一个更清晰的数学问题：在从 \(1\) 到 \(w-1\) 的石头序列中，找出所有长度为 \(l\) 的连续子序列，并计算哪个子序列的石头总数最少。这个最少的石头数，就是答案。
参考代码
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
int main()
{
int w, l; scanf("%d%d", &w, &l);
vector<int> a(w);
int sum = 0, ans = -1;
for (int i = 1; i < w; i++) {
scanf("%d", &a[i]);
sum += a[i];
if (i >= l) {
if (ans == -1) ans = sum;
else ans = min(ans, sum);
sum -= a[i - l + 1];
}
}
printf("%d\n", ans);
return 0;
}
习题：P8775 [蓝桥杯 2022 省 A] 青蛙过河
解题思路
首先进行一个模型转换：让一只青蛙来回往返 \(2x\) 趟等价于让 \(2x\) 只青蛙同时一趟过去，于是就有了类似于前面那题的分析方式。
区别是：本题相当于求这个“窗口”的长度，使得每个窗口内的高度和都大于等于 \(2x\)。
可以枚举每个左端点 \(i\)，用另一个指针 \(j\) 去滑动得到区间和刚刚好够 \(2x\) 的位置，则这些窗口中的最大长度就是青蛙需要的最低跳跃能力。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n, x; scanf("%d%d", &n, &x);
x *= 2;
vector<int> h(n);
for (int i = 1; i < n; i++) {
scanf("%d", &h[i]);
}
int ans = 0, j = 1, sum = 0;
for (int i = 1; i < n; i++) {
while (j < n && sum < x) {
sum += h[j]; j++;
}
if (j == n && sum < x) ans = max(ans, j - i + 1);
else ans = max(ans, j - i);
sum -= h[i];
}
printf("%d\n", ans);
return 0;
}
习题：P1650 田忌赛马
解题思路
首先，一个至关重要的步骤是将双方的马按速度从小到大排序，这样后面就能够方便地比较双方的“最快马”和“最慢马”，为后续的贪心决策提供了清晰的局面。
排序后，可以使用四个指针分别指向田忌和齐王当前最慢和最快的马，从而动态地做出决策。
在每一轮比赛中，都根据这四匹马的情况，按照以下优先级顺序做出最优的贪心选择。
- 上策（用最差的马赢）：比较双方最慢的马，如果田忌的最慢马能赢齐王的最慢马，就直接赢下这一局，为更强的马保存实力。所以，立即进行这场比赛。
- 中策（用最好的马赢）：如果上策不成立，再比较双方最快的马。如果田忌的最快马能赢齐王的最快马，这说明最快马一定能带来一场胜利。（这里可能有个疑问是如果不止一匹马能赢齐王的最快马还是否需要出动田忌的最快马？实际上这种情况下就算先用最快马赢齐王的最快马，那匹田忌第二快的马依然能赢齐王剩下的马，所以不会影响后续的胜负）
- 下策（战略性牺牲）：如果上面两种必胜的情况都不存在，为了最大化整体利益，必须做出一个“牺牲”来尽可能减少损失。最佳策略是，用田忌最慢的马去对阵齐王最快的马，这是一场必输的比赛，但它的战略意义在于“消耗”掉了对方最强的马，从而为田忌其他（相对较好）的马在后续比赛中创造了战胜对方较弱马的机会，这是一种经典的“弃子保帅”策略。
参考代码
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 2005;
int a[N], b[N]; // a：田忌的马速，b：齐王的马速
int main()
{
int n;
scanf("%d", &n); // 读取马的数量
// 读取田忌和齐王的马速
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) scanf("%d", &b[i]);
// 1. 排序
// 将双方的马按速度从小到大排序，这是贪心策略的基础
sort(a + 1, a + n + 1);
sort(b + 1, b + n + 1);
int ans = 0; // 记录田忌的净胜场次（赢+1，输-1，平+0）
// 2. 双指针贪心决策
int p1 = 1, q1 = n; // p1，q1：指向田忌最慢和最快的马
int p2 = 1, q2 = n; // p2，q2：指向齐王最慢和最快的马
for (int i = 1; i <= n; i++) { // 进行 n 轮比赛
if (a[p1] > b[p2]) { // 决策 1（上策）：用田忌最慢的马去赢齐王最慢的马
p1++; p2++; // 消耗双方最慢的马
ans++; // 净胜场+1
} else if (a[q1] > b[q2]) { // 决策 2（中策）：用田忌最快的马去赢齐王最快的马
q1--; q2--; // 消耗双方最快的马
ans++; // 净胜场+1
} else { // 决策 3（下策）：两种稳赢策略都不可行，进行战略性牺牲
// 用田忌最慢的马 a[p1] 去对阵齐王最快的马 b[q2]
// 这是为了用最小的代价消耗掉对方的最强战力
if (a[p1] < b[q2]) {
ans--; // 净胜场-1（输一场）
}
// 如果 a[p1] == b[q2]，则是平局，ans 不变
p1++; // 消耗田忌最慢的马
q2--; // 消耗齐王最快的马
}
}
printf("%d\n", ans * 200); // 每净胜一场得200银币
return 0;
}
习题：P1493 分梨子
解题思路
首先来分析这个核心的约束条件：\(C_1 (A_i - A_0) + C_2 (B_i - B_0) \le C_3\)，其中 \(A_0\) 和 \(B_0\) 是所选子集中，\(A\) 属性和 \(B\) 属性的最小值。这个公式可以变形为：\(C_1 A_i + C_2 B_i \le C_1 A_0 + C_2 B_0 + C_3\)。
定义一个梨子的“特征值” \(F_i = C_1 A_i + C_2 B_i\)，那么约束条件就变成了：对于所有被选中的梨子 \(i\)，都必须满足 \(F_i \le C_1 A_0 + C_2 B_0 + C_3\)。
这个条件说明，一个梨子集合是否合法，完全由这个集合中 \(A\) 属性最小的梨子（称之为梨子 a）和 \(B\) 属性最小的梨子（称之为梨子 b）共同决定。一旦梨子 a 和梨子 b 确定了，\(A_0\) 和 \(B_0\) 就确定了，那么筛选的上限 \(G = C_1 A_0 + C_2 B_0 + C_3\) 也随之确定。所有满足 \(F_i \le G\) 的梨子都可以被圈进来。
但是，这里有一个循环定义的陷阱：选出的集合决定了 \(A_0\) 和 \(B_0\)，而 \(A_0\) 和 \(B_0\) 又反过来决定了哪些梨子可以被选。
为了打破这个循环，可以采用枚举的思想。既然集合的性质由 \(A_0\) 和 \(B_0\) 决定，那就尝试去固定这两个基准值。
一个集合的 \(A_0\) 必然是该集合中某个梨子的 \(A\) 值，\(B_0\) 也必然是该集合中某个梨子的 \(B\) 值。所以，可以做出一个大胆但有效的简化：枚举每一个梨子 \(i\) 作为决定 \(A_0\) 的那个梨子，即假设 \(A_0 = A_i\)。
当固定了 \(A_0\) 后，所有 \(A\) 值小于 \(A_0\) 的梨子都不能被选择，只在 \(A_j \ge A_0\) 的梨子中进行挑选。这时还需要确定 \(B_0\)，此时可以再次枚举所有满足 \(A_j \ge A_0\) 的梨子 \(j\)，让它来临时决定 \(B_0\)，即 \(B_0 = B_j\)。
这样，对于固定的 \(A_0\) 和临时的 \(B_0\)，就得到了一个筛选上限 \(G = C_1 A_0 + C_2 B_0 + C_3\)。任务就变成了：在所有满足 \(A_k \ge A_0\) 的梨子中，统计有多少个梨子 \(k\) 满足 \(F_k \le G\)。
这个“统计”过程如果每次都暴力做，效率很低，这里可以用双指针思想来优化。
将所有梨子按 \(B\) 属性从小到大排序，这有助于固定 \(A_0\) 后，有序地枚举 \(B_0\)。
在固定了 \(A_0\) 的情况下，按排序后的顺序遍历每个梨子，这样就相当于是按 \(B_0\) 递增的顺序进行的。对于每一个 \((A_0, B_0)\) 组合，计算出筛选的上限 \(G = C_1 A_0 + C_2 B_0 + C_3\)。现在，需要在所有满足 \(A_k \ge A_0\) 的梨子中，统计有多少个满足 \(F_k \le G\)。
注意到当 \(B_0\) 增大时，\(G\) 也会增大。这意味着如果有一个按 \(F\) 值排序的梨子顺序，用一个指针控制边界，则这个指针不需要回退。因此时间复杂度可以做到 \(O(n^2)\)。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 2005;
int sum[MAXN], n, f[MAXN];
bool ok[MAXN];
struct Pear {
LL a, b, f;
};
Pear p[MAXN];
bool cmp_b(const Pear& a, const Pear& b) {
return a.b < b.b;
}
bool cmp_f(int i, int j) {
return p[i].f < p[j].f;
}
int main()
{
LL c1, c2, c3;
scanf("%d%lld%lld%lld", &n, &c1, &c2, &c3);
for (int i = 1; i <= n; i++) {
scanf("%lld%lld", &p[i].a, &p[i].b);
p[i].f = c1 * p[i].a + c2 * p[i].b;
}
sort(p + 1, p + n + 1, cmp_b);
for (int i = 1; i <= n; i++) f[i] = i;
sort(f + 1, f + n + 1, cmp_f); // 索引排序
int ans = 0;
for (int i = 1; i <= n; i++) {
LL a0 = p[i].a; // 固定 A0
int cnt = 0;
// 标记所有 A 属性不小于 A0 的梨子为可选
for (int j = 1; j <= n; j++) ok[j] = p[j].a >= a0;
int k = 1; // k 是指向按 F 值排序的索引数组的指针，用于双指针优化
// 内层循环：枚举每个梨子j，假设它的B属性是选定集合的B0
// 由于已经按B值排序，所以这个循环实际上是按B0递增的顺序进行的
for (int j = 1; j <= n; j++)
if (p[j].a >= a0) { // 只考虑那些A属性不小于A0的梨子作为B0的决定者
LL b0 = p[j].b; // 固定B0
LL g = c1 * a0 + c2 * b0 + c3; // 计算筛选上限
// 双指针核心：移动k，将所有满足F值条件的梨子纳入统计
// 因为B0递增，G也递增，所以k指针永不回退
while (k <= n && p[f[k]].f <= g) {
cnt += ok[f[k]]; // 如果这个梨子是可选的（A值满足条件），则计数器增加
ok[f[k]] = false; // 标记为已处理，防止重复计数
k++;
}
ans = max(ans, cnt);
// 在进入下一次内层循环前，处理梨子j本身
// 梨子j在这次循环中是决定B0的基准，但在下次循环中它将成为一个普通的被筛选梨子
if (ok[j]) ok[j] = false; // 如果它之前是可选的（即还没被k指针处理），现在标记为已处理
else cnt--; // 如果是已经计数过的梨子，则需要移除它，这样才能让B0过渡到下一个梨子
}
}
printf("%d\n", ans);
return 0;
}
浙公网安备 33010602011771号