哈希表

哈希表（Hash Table）—— 核心思想与原理

哈希表是一种追求极致速度的数据结构，它的核心目标是实现近乎常数时间复杂度 \(O(1)\) 的插入、删除和查找操作。

一、基本思想：像一个智能储物柜

想象一个智能储物柜，存东西时不需要自己找空柜子，而是直接告诉系统身份标识（键 Key），系统通过一个“神奇算法”（哈希函数 Hash Function）瞬间计算出应该使用的柜子编号（数组索引），然后直接去那个柜子存取物品。

• 键（Key）：要存储或查找的数据的唯一标识。
• 哈希函数（Hash Function）：一个“魔法”函数，它能接收一个键，并将其转换成一个固定范围内的整数（数组索引）。一个好的哈希函数应该快速且均匀（将不同的键散布到数组各处）。
• 数组（Array / Bucket Array）：实际存储数据的容器，也叫“桶”。

二、核心问题：哈希冲突（Hash Collision）

理想情况下，每个键都对应一个独一无二的柜子。但现实是，不同的键（比如两个不同的单词）经过哈希函数计算后，可能会得到相同的数组索引。这种情况就叫做哈希冲突。

三、解决冲突

解决冲突最经典的方法是拉链法。

• 思想：不再让数组的每个位置只存一个元素，而是让每个位置都挂一个链表。
• 过程：
  1. 当一个新元素要插入时，通过哈希函数计算出索引 \(i\)。
  2. 直接将这个新元素添加到 \(i\) 位置上挂着的那个链表的末尾。
  3. 当查找一个元素时，先通过哈希函数找到索引 \(i\)，然后遍历这个位置的链表，直到找到目标元素。

总结：哈希表通过空间换时间，利用哈希函数实现快速定位，并通过拉链法等方式解决冲突，从而在平均情况下达到了 \(O(1)\) 的惊人性能。

除了拉链法，开放地址法也是一种解决冲突的经典策略。它的核心思想是，当发生哈希冲突时，不在当前位置挂上一个链表，而是在哈希表内部寻找下一个可用的空位置来存放元素。

• 思想：如果通过哈希函数计算出的柜子已被占用，就按照一套预定的规则去寻找下一个、再下一个……直到找到一个空柜子为止。所有元素都必须存放在哈希表这个主数组内。
• 过程：这个寻找下一个空位的过程被称为探测。根据探测规则的不同，开放地址法又分为几种具体实现：
  • 线性探测：如果位置 \(k\) 被占用，就依次检查 \(k+1, k+2, k+3, \dots\)
  • 平方探测：跳跃式地检查 \(k+1^2, k+2^2, k+3^2, \dots\)
  • 双重哈希：使用第二个哈希函数来确定每次探测地固定步长。

与拉链法相比，开放地址法将所有数据都保存在数据中，因此缓存性能更好，也无需存储额外的指针。但它的缺点是容易产生“聚集”现象（即冲突的元素堆在一起），并且在数据删除时处理起来更为复杂。

无论是拉链法还是开放地址法，哈希表的性能都受到一个关键指标的影响，那就是装载因子。它衡量了哈希表的“拥挤”程度。

• 定义：装载因子 \(\alpha\) 的计算公式是 \(\alpha = 哈希表中已存入的元素数量 / 哈希表的总槽位数\)。

简单来说，它表示哈希表在多大程度上被填满了。这个指标对于不同冲突解决方法的影响有着天壤之别。

• 在拉链法中：装载因子可以大于或等于 1。例如，当 \(\alpha = 2\) 时，它仅仅意味着每个槽位平均挂了 2 个元素。虽然链表变长会导致查找时间增加，但性能的下降是平缓的、可预测的。
• 在开放地址法中：装载因子是决定性能的生命线，它必须严格小于 1。因为所有元素都存储在住数组中，一旦装载因子过高（例如超过 0.8）时，就需要进行扩容——即创建一个更大的数组，并将所有元素重新计算哈希值后放入新数组中。这是一个成本较高的操作，但它确保了哈希表在后续使用中能够继续提供高效的性能。

---

选择题：广度优先搜索时，一定需要用到的数据结构是？

• A. 栈
• B. 二叉树
• C. 队列
• D. 哈希表

答案

C。

BFS 的特点是逐层扩展或辐射式的搜索。它必须处理完同一层的所有状态，然后才能进入下一层。

为了实现“逐层扩展”，算法需要一个能够记录“待访问”节点的列表，并且这个列表必须遵循先发现，先访问的原则。这正是一种先进先出的数据结构。

队列是一种先进先出的数据结构，完美契合 BFS 的需求。

栈是一种后进先出的数据结构。如果使用栈，算法会优先访问最新发现的状态，从而深度到某个分支，直到无法再深入才回溯。这实现的是深度优先搜索，而不是广度优先搜索。

二叉树是一种被遍历的对象，而不是用来实现遍历算法的辅助工具。BFS 算法可以应用在二叉树上，但二叉树本身不是实现 BFS 所需的数据结构。

在实现 BFS 时，通常需要一个数据结构来记录哪些节点已经被访问过，以避免重复访问和陷入死循环。哈希表（或布尔数组）因其高效的查询效率而常被用来实现这个“已访问集合”。但是，它并不是驱动 BFS 算法“逐层”搜索的核心。这个核心角色是由队列扮演的。虽然哈希表很有用，但并非“一定需要”（例如，可以用其他方式记录访问状态），而没有队列就无法实现 BFS 的核心逻辑。

---

选择题：在设计一个哈希表时，为了减少冲突，需要使用适当的哈希函数和冲突解决策略。已知某哈希表中有 \(n\) 个键值对，表的装载因子为 \(\alpha \ (0 \lt \alpha \le 1)\)。在使用开放地址法解决冲突的过程中，最坏情况下查找一个元素的时间复杂度为？

• A. \(O(1)\)
• B. \(O(\log n)\)
• C. \(O(1/(1 - \alpha))\)
• D. \(O(n)\)

答案

D。这个问题问的是最坏情况下的时间复杂度，需要考虑最不利的元素分布情况。

1. 开放地址法的核心：当发生冲突时，算法会探测哈希表中的其他槽位，直到找到目标元素或一个空槽位（表示查找失败）。
2. 最坏情况的构建：想象一个极端情况，由于哈希函数和插入顺序的“不幸”组合，导致所有 \(n\) 个插入的键形成了一个连续的探测序列（或称为“聚集”）。
   • 例如，在使用线性探测时，可能所有 \(n\) 个元素恰好被连续地存放在了索引为 \(k, k+1, k+2, \dots, k+n-1\) 的位置。
3. 查找过程：现在，假设要查找一个元素。
   • 情况一（查找成功）：要查找的元素恰好是这个聚集中的最后一个元素。算法必须从这个聚集的起点开始，逐一探测，直到检查完所有 \(n\) 个元素，才最终找到它。
   • 情况二（查找失败）：要查找一个不存在的元素，而它的哈希值恰好是这个聚集的起始位置。算法必须完整探测完整个聚集中的所有 \(n\) 个元素，直到最终遇到一个空槽位，才能断定该元素不存在。

在这两种最坏情况下，查找操作都需要检查 \(n\) 个元素。因此，时间复杂度与哈希表中的元素数量 \(n\) 成正比。

---

选择题：给定地址区间为 0~9 的哈希表，哈希函数为 h(x) = x % 10，采用线性探查的冲突解决策略（对于出现冲突情况，会往后探查第一个空的地址存储；若地址 9 冲突了则从地址 0 重新开始探查）。哈希表初始为空表，依次存储 71, 23, 73, 99, 44, 79, 89 后，请问 89 存储在哈希表哪个地址中？

• A. 9
• B. 0
• C. 1
• D. 2

答案

D

---

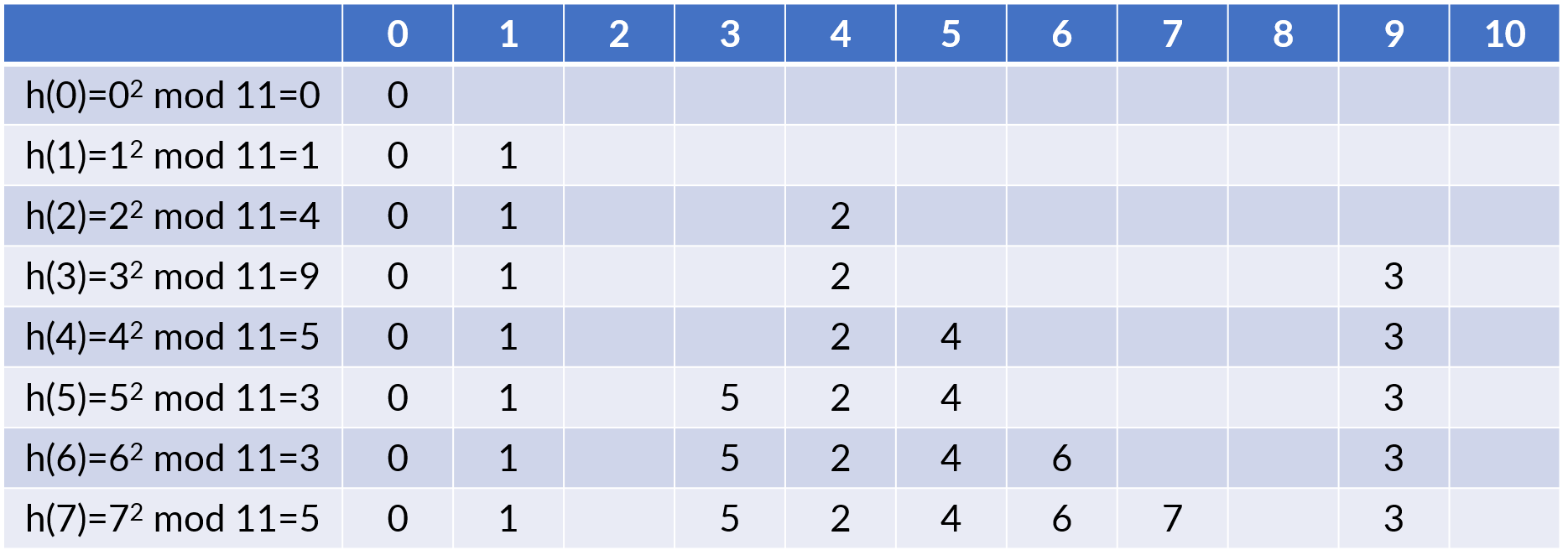
选择题：现有一个地址区间为 0~10 的哈希表，对于出现冲突情况，会往后找第一个空的地址存储（到 10 冲突了就从 0 开始往后），现在要依次存储 0,1,2,3,4,5,6,7，哈希函数为 \(h(x) = x^2 \bmod 11\)。请问 7 存储在哈希表哪个地址中？

• A. 5
• B. 6
• C. 7
• D. 8

答案

C。

---

选择题：将 2,7,10,18 分别存储到某个地址区间为 0~10 的哈希表中，如果哈希函数是哪个选项，将不会产生冲突，其中 \(a \bmod b\) 表示 a 除以 b 的余数。

• A. \(x^2 \bmod 11\)
• B. \(2x \bmod 11\)
• C. \(x \bmod 11\)
• D. \(\left\lfloor \dfrac{x}{2} \right\rfloor \bmod 11\)，其中 \(\left\lfloor \dfrac{x}{2} \right\rfloor\) 表示 \(\dfrac{x}{2}\) 下取整

答案

D。

需要将待存储的四个数分别代入四个选项给出的哈希函数中，计算它们的哈希地址。如果对于一个函数，所有关键字计算出的地址都不相同，那么这个函数就不会产生冲突。

A、B、C 选项 h(7) 和 h(18) 计算出来都是相等的，只有 D 选项的哈希函数不会产生冲突。

---

C++ 中的 unordered 家族容器

C++ 标准库提供了四个基于哈希表实现的容器，它们都具有 \(O(1)\) 的时间复杂度，且内部元素都是无序的。

一、unordered_set —— 高效的“不重复元素集合”

• 特点：存储唯一的元素（键）。
• 用途：快速判断一个元素是否存在、高效地去除序列中的重复元素。

void unordered_set_demo() {
    cout << "--- 1. std::unordered_set Demo (Unique Keys) ---\n";
    unordered_set<string> s;
    s.insert("apple"); 
    s.insert("banana");
    s.insert("apple"); // 重复插入，无效
    cout << "Set size: " << s.size() << "\n"; // 输出: 2
    if (s.count("banana")) { // .count() 返回 0 或 1
        cout << "'banana' exists.\n";
    }
    s.erase("apple"); 
    cout << "After erasing 'apple', size is: " << s.size() << "\n"; // 输出：1
}

二、unordered_multiset —— 高效的“可重复元素集合”

• 特点：允许存储重复的元素（键）。
• 用途：统计每个元素出现的次数，或者存储一个允许重复的“袋子”。

void unordered_multiset_demo() {
    cout << "--- 2. std::unordered_multiset Demo (Duplicate Keys Allowed) ---\n";
    unordered_multiset<string> ms;
    ms.insert("apple");
    ms.insert("banana");
    ms.insert("apple"); // 重复插入，有效
    cout << "Multiset size: " << ms.size() << "\n"; // 输出: 3
    cout << "Count of 'apple': " << ms.count("apple") << "\n"; // 输出: 2
    ms.erase("apple"); // 注意：这会删除所有 "apple"
    cout << "After erasing all 'apple', size is: " << ms.size() << "\n"; // 输出：1
}

三、unordered_map —— 高效的“键值对字典”

• 特点：存储唯一的键和与之关联的值（Key-Value Pair）。
• 用途：建立从键到值的映射关系，如字典、词频统计、缓存等。

void unordered_map_demo() {
    cout << "\n--- 3. std::unordered_map Demo (Unique Key-Value Pairs) ---\n";
    unordered_map<string, int> m;
    // 使用 [] 运算符插入或更新
    m["Alice"] = 95;
    m["Bob"] = 88;
    m["Alice"] = 98; // 更新 Alice 的分数
    cout << "Alice's score: " << m["Alice"] << "\n"; // 输出: 98
    cout << "Map size: " << m.size() << "\n"; // 输出: 2
    // 遍历
    for (const auto& p : m) {
        cout << p.first << ": " << p.second << "\n"; 
    }
}

四、unordered_multimap —— 高效的“可重复键值对字典”

• 特点：允许存储重复的键，每个键可以关联多个不同的值。
• 用途：建立一对多的映射关系，如一个单词有多个释义、一个人有多个电话号码。
• 注意：由于键可重复，multimap 没有 [] 操作符。

void unordered_multimap_demo() {
    cout << "4. unordered_multimap Demo (Duplicate Key-Value Pairs Allowed)\n";
    unordered_multimap<string, string> mm;
    mm.insert({"word", "a unit of language"});
    mm.insert({"word", "a promise of language"});
    mm.insert({"book", "a written or printed work"});
    cout << "Content of key 'word': " << mm.count("word") << "\n"; // 输出: 2
    // 查找所有键为 "word" 的条目
    auto range = mm.equal_range("word");
    cout << ("Definitions for 'word': \n");
    for (auto it = range.first; it != range.second; it++) {
        cout << "  - " << it->second << "\n";
    }
}

一句话总结：

• set 只存键，map 存键值对。
• set 和 map 的键是唯一的，multiset 和 multimap 的键可以重复。

当需要极快的查找速度，并且不关心元素顺序时，unordered 家族就是首选。根据需求（是否需要值、是否允许键重复）来选择合适的容器。

#include <iostream>
#include <string>
#include <unordered_set>
#include <unordered_map>
using namespace std;
// 主函数调用上面的所有示例
int main()
{
    unordered_set_demo();
    unordered_multiset_demo();
    unordered_map_demo();
    unordered_multimap_demo();
    return 0;
}

---

习题

P1571 眼红的Medusa

解题思路

这个问题要求找出两个获奖名单中都出现的人员编号，即求两个集合的交集。同时，输出的顺序必须遵循第一个名单（科技创新奖）中的出现顺序。

将 \(n\) 个科技创新奖获得者的编号，按顺序读入一个普通的数组。使用数组的目的是为了完整保留它们的原始输入顺序，因为题目对输出顺序有要求。

创建一个 unordered_set 容器，然后，读取 \(m\) 个特殊贡献奖获得者的编号，并将每一个编号都插入到这个哈希集合中。哈希集合的特点是，它能够以极高的效率判断某个元素是否存在于集合中。

从头到尾遍历一开始存储的数组，对于数组中的每一个编号，都去哈希集合中查询它是否存在。如果查询结果为“存在”，就说明这个编号同时也出现在第二个名单里，即为同时获得两个奖项的人。此时，立即将这个编号输出。

因为是严格按照第一个名单的顺序进行遍历和判断的，所以一旦找到一个共同的编号，就立即输出。这天然地保证了最终输出的编号顺序与在第一个名单中的顺序完全一致，满足了题目要求。

参考代码

#include <cstdio>
#include <unordered_set>
using namespace std;
const int N = 100005;
// 数组 a 用于存储科技创新奖的名单，关键作用是保持原始输入顺序
int a[N]; 
int main()
{
    int n, m; 
    scanf("%d%d", &n, &m); // 读取两个名单的人数

    // 步骤1: 读取科技创新奖名单到数组 a
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }

    // 步骤2: 使用哈希集合存储特殊贡献奖名单
    // unordered_set 提供近乎 O(1) 的平均时间复杂度的查找操作，是本题的关键
    unordered_set<int> s;
    for (int i = 1; i <= m; i++) {
        int x; 
        scanf("%d", &x); // 读取编号
        s.insert(x);     // 将编号插入到哈希集合中，用于快速查找
    }

    // 步骤3: 遍历科技创新奖名单，查找同时获奖的人
    // 严格按照 a 数组的顺序遍历，这就保证了输出顺序的正确性
    for (int i = 1; i <= n; i++) {
        // s.count(a[i]) 会在哈希集合中查找 a[i] 是否存在。
        // 如果存在，count返回1；否则返回0。
        if (s.count(a[i])) {
            // 如果存在，说明此人获得了两个奖项，按题目要求输出
            printf("%d ", a[i]);
        }
    }
    
    return 0;
}