图论基础
图是若干个顶点和若干条边构成的数据结构，顶点是实际对象的抽象，边是对象之间关系的抽象。可以将图形式化表示为二元组 \(G = (V,E)\)，其中，\(V\) 是顶点集，表征数据元素；\(E\) 是边集，表征数据元素之间的关系。信息学竞赛中一般使用 \(n\) 表示图中结点的数量，使用 \(m\) 表示图中边的数量。
图可以分为无向图（undirected graph）、有向图（directed graph）、混合图（mixed graph）。无向图的边集 \(E\) 中的每个元素是一个无序二元组 \((u,v)\)，称作无向边（undirected edge），简称边（edge），其中 \(u\) 和 \(v\) 称为端点（endpoint）。有向图的边集 \(E\) 中的每个元素是一个有序二元组 \((u,v)\)，称作有向边（directed edge）或弧（arc），其中 \(u\) 称为弧尾，\(v\) 称为弧头。混合图中的边集既有无向边也有有向边。
在无向图中，若任意两个顶点之间都存在边，则该无向图称为完全无向图。\(n\) 个顶点的无向完全图，一共有 \(n(n-1)/2\) 条边。在有向图中，若任意两个顶点 \(x,y\)，既存在 \(x\) 到 \(y\) 的弧，也存在 \(y\) 到 \(x\) 的弧，则该有向图称为有向完全图。\(n\) 个顶点的有向完全图，一共有 \(n(n-1)\) 条弧。
选择题：设有一个 10 个顶点的完全图，每两个顶点之间都有一条边。有多少个长度为 4 的环？
- A. 120
- B. 210
- C. 630
- D. 5040
答案
C。这是一个组合数学问题。可以分两步来解决。
第一步：选择构成环的 4 个顶点
一个长度为 4 的环需要 4 个不同的顶点。首先需要从 10 个顶点中选出 4 个。这是一个组合问题，因为选择顶点的顺序无关紧要。
选择 4 个顶点的方式数等于 \(C_{10}^4 = \dfrac{10!}{4!(10-4)!} = \dfrac{10!}{4!6!} = \dfrac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1} = 210\)
所以，有 210 种不同的方式来选择 4 个顶点。
第二步：用选出的 4 个顶点构成环
假设已经选出了 4 个顶点，比如 {A,B,C,D}。因为这是一个完全图，所以这 4 个顶点中的任意两个之间都有一条边。
现在的问题是，用这 4 个顶点能构成多少个不同的长度为 4 的环？
固定一个顶点作为起点，比如 A。从 A 出发，可以选择 B、C、D 中的任意一个作为下一个顶点（3 个选择）。
- 假设选择了 B。
- 从 B 出发，不能回到 A（否则会形成长度为 2 的环），所以可以在 C 和 D 中选择一个（2 个选择）。
- 假设选择了 C。
- 从 C 出发，只能去 D（1 个选择）。
- 最后从 D 回到 A，形成环 A-B-C-D-A。
这样看来，似乎有 \(3 \times 2 \times 1 = 6\) 种排列方式。但是，环 A-B-C-D-A 和环 A-D-C-B-A 是同一个环，只是遍历方向相反。所以需要将结果除以 2，\(6 / 2 = 3\)。
因此，对于任意选定的 4 个顶点，都可以构成 3 个不同的环，这 3 个环分别是：A-B-C-D-A，A-B-D-C-A，A-C-B-D-A。
第三步：计算总数
将第一步和第二步的结果相乘，总环数等于 630。
所以，在一个 10 个顶点的完全图中，共有 630 个长度为 4 的环。
选择题：G 是一个非连通无向图（没有重边和自环），共有 28 条边，则该图至少有多少个顶点？
- A. 10
- B. 9
- C. 11
- D. 8
答案
B。
为了让顶点数最少，应该让图的“密度”尽可能大，即在固定的顶点上尽可能多地连边。
一个有 \(n\) 个顶点的简单图，最多的边数存在于完全图 \(K_n\) 中，其边数为 \(n(n-1)/2\)。
假设图是连通的，找需要多少顶点才能容纳 28 条边。对于 \(n=8\)，一个完全图 \(K_8\) 的边数为 \(8 \times 7 / 2 = 28\)。一个有 8 个点、28 条边的简单图是完全图 \(K_8\)，而 \(K_8\) 是一个连通图。这与题目要求的“非连通”矛盾，所以顶点数必须大于 8。再 \(K_8\) 的基础上补一个孤点即可，因此最少 9 个点。
选择题：G 是一个非连通简单无向图（没有自环和重边），共有 36 条边，则该图至少有多少个点？
- A. 8
- B. 9
- C. 10
- D. 11
答案
C。
在无向图中，若点 \(u\) 与点 \(v\) 存在边 \((u,v)\)，则顶点 \(v\) 和顶点 \(u\) 互称为邻接点。在有向图中，若点 \(u\) 与点 \(v\) 之间存在一条点 \(u\) 指向点 \(v\) 的一条弧 \((u,v)\)，则称顶点 \(u\) 邻接到顶点 \(v\)，顶点 \(v\) 邻接自顶点 \(u\)。
与顶点相关联的边的数目或者弧的数目称为该顶点的度。在无向图中，顶点的度就是其关联的边的数目。在有向图中，由于与顶点关联的弧具有方向性，因此要区分顶点的入度和出度。入度指以该顶点为弧头的弧的数目，而出度指以该顶点为弧尾的弧的数目，入度与出度之和是该顶点的度。
答案
6 号结点，度为 4
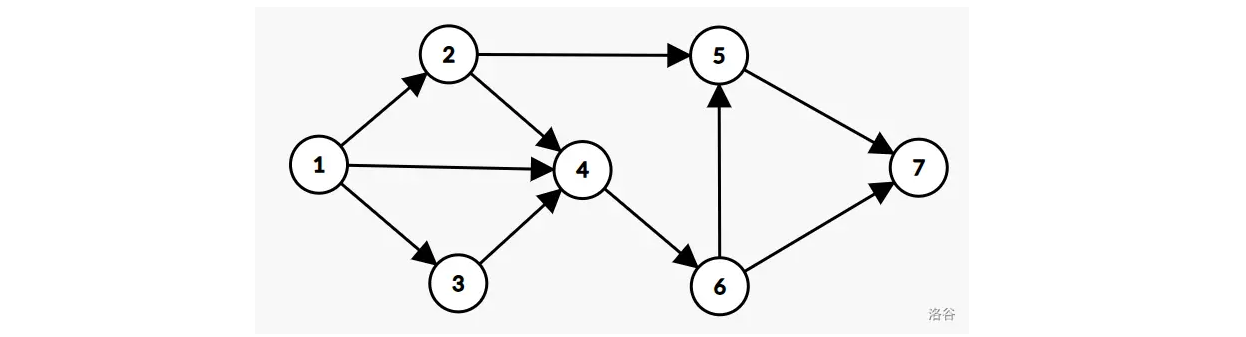
选择题：如图是一张包含 7 个顶点的有向图，如果要删除其中一些边，使得从节点 1 到节点 7 没有可行路径，且删除的边数最少，请问总共有多少种可行的删除边的集合？
- A. 1
- B. 2
- C. 3
- D. 4
答案
D。删除边 \((2,5)\) 和 \((4,6)\)；删除边 \((1,2)\) 和 \((4,6)\)；删除边 \((4,6)\) 和 \((5,7)\)；删除边 \((5,7)\) 和 \((6,7)\)。
选择题：假设 \(n\) 是图的顶点的个数，\(m\) 是图的边的个数，为求解某一问题有下面四种不同时间复杂度的算法。对于 \(m = \Theta (n)\) 的稀疏图而言，下面的四个选项，哪一项的渐近时间复杂度最小？
- A. \(O(m \sqrt{\log n} \cdot \log \log n)\)
- B. \(O(n^2 + m)\)
- C. \(O(\dfrac{n^2}{\log m} + m \log n)\)
- D. \(O(m + n \log n)\)
答案
稀疏图意味着时间复杂度式子里的 \(m\) 可以统一替换成 \(n\) 来处理。当 \(n\) 趋近于无穷时，\(\log \log n\) 的增长速度显然小于 \(\sqrt{\log n}\)，因此 A 选项不会超过 \(n \log n\)，所以答案选 A。
邻接矩阵
邻接矩阵是图的一种存储方式，用一个二维数组存放图中的全部边，以数组中的下标对应顶点。邻接矩阵中的矩阵元素 \(A_{i,j}\) 存放了顶点 \(i\) 和顶点 \(j\) 之间的关系。若图是无向图，则 \(A_{i,j}\) 和 \(A_{j,i}\) 同时存放顶点 \(i\) 与顶点 \(j\) 之间的边，若图是有向图，则 \(A_{i,j}\) 存放顶点 \(i\) 到顶点 \(j\) 的有向边。
对于无权图，邻接矩阵元素 \(A_{i,j}\) 定义为：
对于带权图，邻接矩阵元素 \(A_{i,j}\) 定义为：
邻接矩阵存储具有以下特征：
- 无向图的邻接矩阵是对称矩阵，有向图的邻接矩阵是非对称矩阵
- 对于无向图，其邻接矩阵第 \(i\) 行（或第 \(i\) 列）非零元素的个数正好是第 \(i\) 个顶点的度
- 对于有向图，其邻接矩阵第 \(i\) 行非零元素的个数正好是第 \(i\) 个顶点的出度，而第 \(j\) 列非零元素的个数正好是第 \(j\) 个顶点的入度。
对于 \(n\) 个顶点的图，采用邻接矩阵存储，需要占用 \(n \times n\) 个存储单元，其空间复杂度为 \(O(n^2)\)。
选择题：以下哪个结构可以用来存储图？
- A. 栈
- B. 二叉树
- C. 队列
- D. 邻接矩阵
答案
D。
例题：P5318 【深基18.例3】查找文献
小 K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干（也有可能没有）参考文献的链接指向别的博客文章。小 K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献就不用再看它了）。
假设洛谷博客里面一共有 \(n \ (n \le 10^5)\) 篇文章（编号为 \(1\) 到 \(n\)）以及 \(m \ (m \le 10^6)\) 条参考文献引用关系。目前小 K 已经打开了编号为 \(1\) 的一篇文章，输出 DFS、BFS 两种遍历方式下看文章的顺序（当有多篇参考文章时，先看编号小的）。
题目描述的是一个有向图，其中“参考文献”关系 \(X \rightarrow Y\) 可以看作是从节点 \(X\) 到节点 \(Y\) 的一条有向边。可以使用邻接表（vector<vector<int>> g）来存储这个图。g[u] 是一个列表，包含了所有从节点 u 可以直接到达的节点，这种数据结构非常适合进行图的遍历，可以在读取 n 之后，使用 g.resize(n + 1) 来为邻接表分配所需的空间。
先看编号较小的是本题的关键约束，它要求在遍历时，如果一个节点有多个邻居可以访问，必须先访问编号最小的那个邻居。为了实现这一点，需要确保对于每个节点 u，其在邻接表 g[u] 中的邻居列表是按升序排列的。
DFS 的策略是“一条路走到黑”，它从起始节点出发，访问一个邻居，然后立刻从这个邻居出发继续深入，直到不能再走为止，然后才回溯到上一个节点，尝试访问其尚未访问过的其他邻居。可以使用递归来实现，用一个 vis 数组来标记已访问过的节点，防止重复访问和在有环图中陷入死循环。由于邻接表中已经预先排好序，当循环遍历邻居时，自然就满足了“先访问小编号”的规则。
BFS 的策略是“逐层扩展”，它从起始点出发，先访问完所有与起始点直接相连的邻居，然后再按顺序访问这些邻居的邻居，像水波纹一样一层一层地向外扩散。可以使用队列来实现 BFS，这也是一种比较标准的 BFS 实现方式。同样，需要一个 vis 数组（在 DFS 后需要重置）来标记已访问节点。将起始点 1 入队，当一个节点 u 出队时，就按顺序将其所有未被访问过的邻居入队，因为邻接表是排好序的，所以邻居们被依次入队，也就保证了它们将来被访问的顺序同样满足“先访问小编号”的规则。
参考代码
#include <cstdio>
#include <algorithm>
#include <vector>
#include <queue>
using std::sort;
using std::vector;
using std::queue;
using std::pair;
using Edge = pair<int, int>;
// 节点和边的数量上限
const int N = 1e5 + 5;
const int M = 1e6 + 5;
// e：临时存储所有边的数组，用于一次性排序
// g：邻接表，g[u] 存储从节点 u 出发能到达的所有节点 v
// vis：访问标记数组，vis[u] = true 表示节点 u 已被访问
Edge e[M];
vector<vector<int>> g; // 使用 vector of vector 作为邻接表
bool vis[N];
/**
* @brief 深度优先搜索（DFS）
* @param u 当前访问的节点
*/
void dfs(int u) {
// 标记当前节点为已访问，并立即打印
vis[u] = true; printf("%d ", u);
// 遍历当前节点的所有邻居
// 由于邻接表在构建时已经保证有序，这里会按小编号优先的顺序访问
for (int v : g[u]) {
// 如果邻居节点 v 未被访问过，则递归地对 v 进行 DFS
if (!vis[v]) {
dfs(v);
}
}
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
// 为邻接表分配空间，使其可以容纳 n+1 个节点（从1到n）
g.resize(n + 1);
// 1. 读取所有边，并存储在临时数组 e 中
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
e[i] = {x, y};
}
// 2. 对所有边排序
// 这是本题的关键技巧，排序后，起点相同的边会聚集在一起
// 并且它们的终点是按升序排列的
sort(e + 1, e + m + 1);
// 3. 根据排好序的边数组，构建邻接表
// 这样，每个节点的邻居列表 g[x] 就自动变为了有序的
for (int i = 1; i <= m; i++) {
int x = e[i].first, y = e[i].second;
g[x].push_back(y);
}
// 执行 DFS
dfs(1); printf("\n");
// 重置 vis 数组，为 BFS 做准备
for (int i = 1; i <= n; i++) vis[i] = false;
queue<int> q; // 创建用于BFS的队列
q.push(1); // 将起始节点 1 入队
vis[1] = true; // 标记起始节点为已访问
while (!q.empty()) {
int u = q.front(); // 取出队首元素
printf("%d ", u); // 打印该元素
q.pop(); // 将该元素出队
// 遍历 u 的所有邻居
for (int v : g[u]) {
// 如果邻居 v 从未被访问过
if (!vis[v]) {
q.push(v); // 将 v 入队
vis[v] = true; // 并标记为已访问
}
}
}
printf("\n");
return 0;
}
分析邻接表的组成，存储一个节点 \(u\) 的邻接边，其方法的关键是先定位第 1 条边，第 1 条边处理完再定位第 2 条边，第 2 条边处理完再定位第 3 条边……。根据这个分析，可以设计一种更加紧凑、没有任何空间浪费、实现容易的存图方法。
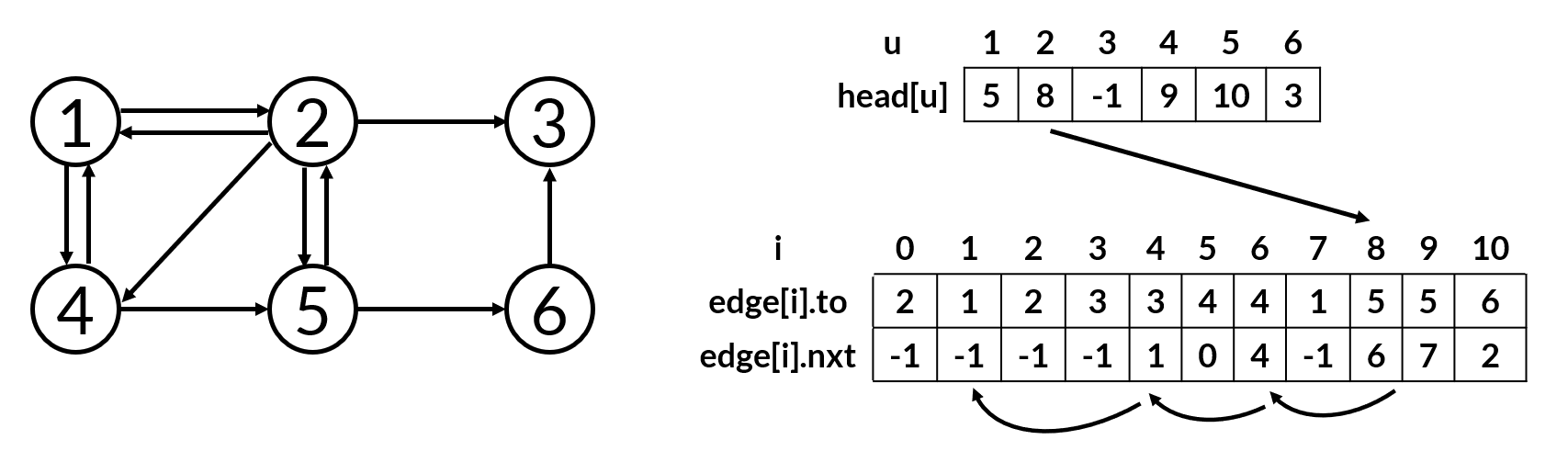
#include <cstdio>
const int N = 1e6 + 5;
const int M = 2e6 + 5;
int cnt, head[N]; // cnt 记录当前存储位置
struct Edge {
// from 为边的起点，一般情况下可以不需要，因为当遍历某个点 u 的出边时，from 始终是 u
// to 为边的终点
// nxt 为 from 的出边里 from->to 之后的下一条边在 edge 数组中的位置
int from, to, nxt, w;
};
Edge edge[M]; // 边数组的大小取决于边的数量，如果存无向图，大小是输入的边的数量的两倍
void init(int n) {
for (int i = 1; i <= n; i++) {
head[i] = -1; // 另一种写法是初始化成 0
// 区别是第一条边存在 edge[0] 还是 edge[1]
}
cnt = 0;
}
void addedge(int u, int v, int w) {
edge[cnt] = {u, v, head[u], w};
head[u] = cnt;
cnt++; // 这样相当于第一条边存在 edge[0] 上，如果想存在 edge[1] 上就把 cnt++; 写成这个函数的第一条语句
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
init(n); // 初始化
for (int i = 0; i < m; i++) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
addedge(u, v, w);
}
for (int i = 1; i <= n; i++) {
printf("head[%d]=%d ", i, head[i]);
}
printf("\n");
for (int i = 0; i < m; i++) {
printf("edge[%d].to / nxt = %d / %d\n", i, edge[i].to, edge[i].nxt);
}
// 遍历节点 2 的所有邻居
printf("2 ->");
for (int i = head[2]; i != -1; i = edge[i].nxt) { // i != -1 也可以写成 ~i
printf(" %d", edge[i].to);
}
return 0;
}
选择题：具有 n 个顶点，e 条边的图采用邻接表存储结构，进行深度优先遍历运算的时间复杂度为？
- A. \(O(n+e)\)
- B. \(O(n^2)\)
- C. \(O(e^2)\)
- D. \(O(n)\)
答案
A。
DFS 算法需要遍历图中的每一个顶点。为了防止重复访问，会使用一个数组来记录顶点的访问状态。在整个算法过程中，每个顶点都只会被访问一次。因此，访问所有 n 个顶点的操作所需的时间复杂度为 \(O(n)\)。
当算法访问到某个顶点 v 时，它需要查找 v 的所有邻接点。在使用邻接表存储时，查找顶点 v 的所有邻接点，相当于访问所有 v 的出边。在整个 DFS 过程中，每条边都只会被遍历一次。因此，遍历所有 e 条边的操作所需的总时间复杂度为 \(O(e)\)。
将访问顶点和遍历边的时间复杂度相加，得到 DFS 在邻接表存储结构下的总时间复杂度 \(O(n+e)\)。
如果图采用的是邻接矩阵存储，那么查找一个顶点的所有邻接点需要遍历矩阵的一整行，耗时为 \(O(n)\)。对所有 \(n\) 个顶点都执行此操作，则总时间复杂度会变为 \(O(n^2)\)。因此，对于稀疏图（边 e 远小于 \(n^2\)），使用邻接表效率要高得多。
程序阅读题：
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int MAXN = 200001;
int main() {
int n, m, l, r, w;
cin >> n >> m;
vector <int> dist(MAXN, -1);
vector <bool> vis(MAXN, false);
vector <vector <pair<int, int> > > go(MAXN);
for (int i = 1; i <= m; i++) {
cin >> l >> r >> w;
go[l].push_back(make_pair(r + 1, w));
go[r + 1].push_back(make_pair(l, -w));
}
queue <int> q;
dist[1] = 0; vis[1] = true;
q.push(1);
while (!q.empty()) {
int x = q.front(); q.pop();
for (auto i : go[x]) {
if (!vis[i.first]) {
vis[i.first] = true;
dist[i.first] = dist[x] + i.second;
q.push(i.first);
}
}
}
if (dist[n + 1] == -1) cout << "sorry" << endl;
else cout << dist[n + 1] << endl;
return 0;
}
假设输入的 \(n,m\) 是不超过 \(200000\) 的正整数，程序第 \(13\) 行每次输入的 \(l,r\) 保证 \(l \le r\)。
判断题
交换程序的第 \(14\) 行与第 \(15\) 行，不影响程序运行的结果。
答案
正确。第 \(14\) 行相当于点 \(l\) 向点 \(r+1\) 连一条权值为 \(w\) 的边，第 \(15\) 行相当于点 \(r+1\) 向点 \(l\) 连一条权值为 \(-w\) 的边。先连哪条边不影响建图的效果。
输入的 \(r\) 的最大值为 \(n\) 时，程序可以正常运行。
答案
错误。数组的大小设定为 \(200001\)，可以使用的最大下标是 \(200000\)，而当输入的 \(r\) 达到 \(200000\) 时，相当于对应的结点 \(r+1\) 是 \(200001\)，下标会越界。
在程序的第 \(17\) 行至第 \(29\) 行，相同的数可能重复进入队列。
答案
错误。进入队列的条件是 !vis[i.first]，一旦进入队列后 vis[i.first]=true，因此不可能重复进队。
单选题
当输入的 \(l\) 最小值为 \(x\)，输入的 \(r\) 最大值为 \(y\) 时，最多有多少个元素进入过队列？
A. 1 / B. y-x / C. y-x+1 / D. y-x+2
答案
D。这个程序相当于建图后从点 \(1\) 开始进行宽度优先搜索。如果输入的每一对 \(l\) 和 \(r\) 都相同的话，相当于点 \(l\) 和 \(l+1\) 之间连边。所以进队最多的情况是：\(x=1\)，点 \(1\) 和点 \(2\) 有连边，点 \(2\) 和点 \(3\) 有连边，以此类推……。那么从 \(1\) 到 \(y+1\) 都进过队列，共有 \(y+1-x+1=y-x+2\) 个元素。
当输入的 \(n\) 为偶数，且 \(r=l+1\) 时，\(m\) 至少为多少时输出不为 sorry？
A. \(n/2\) / B. \(n/2+1\) / C. \(n/2-1\) / D. \(n\)
答案
A。如果 \(r=l+1\)，则每次连边的点之间编号正好差 \(2\)。dist 数组的作用是在宽搜过程中更新从 \(1\) 号点到其他点的距离，根据第 \(30\) 行至第 \(31\) 行，如果最终能够到达 \(n+1\) 号点，则会输出这个距离，到不了（最后 dist[n+1] 等于 -1）则输出 sorry。因此要使得 \(m\) 尽可能小也就是输入的边数尽可能少，对应的情况是 \(1\) 和 \(3\) 连边，\(3\) 和 \(5\) 连边，以此类推……。由于输入的 \(n\) 是偶数，则 \(n+1\) 是奇数，需要的边数正好为 \(n/2\)。
当输入为 5 3 1 3 4 3 4 2 4 5 3 时，输出为？
A. 4 / B. 5 / C. 6 / D. 7
答案
D。根据输入数据建的图如下所示：
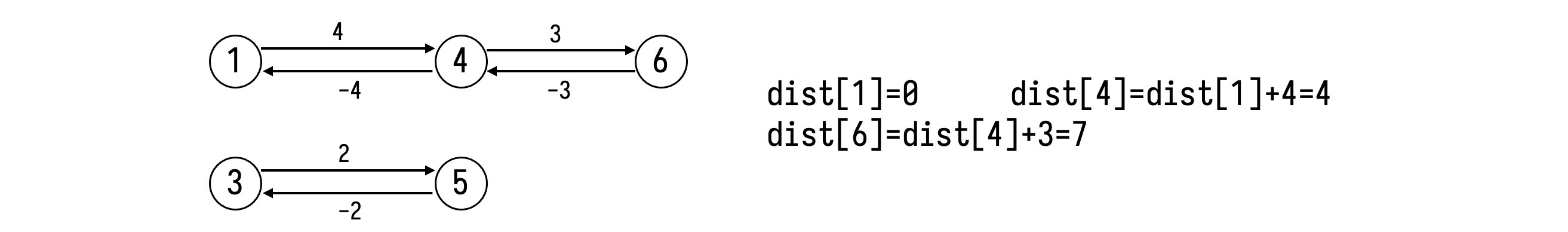
例题：P2097 资料分发 1
题目描述的是一个网络，其中电脑是节点（顶点），双向数据线是边，这构成了一个无向图。“如果一个电脑得到数据，它可以传送到的电脑都可以得到数据”这句话是关键，它描述了数据的传输方式：数据可以在一个连通块内的所有电脑之间自由流动。连通块是什么？在图中，如果从顶点 A 可以到达顶点 B（无论经过多少条边），那么 A 和 B 就属于同一个连通块，一个连通块是图的一个子图，其中任意两个顶点都相互连通。因此，只要向一个连通块中的任意一台电脑输入数据，这个连通块内的所有电脑就都能得到数据。
为了让所有电脑都得到数据，必须确保每个连通块都至少有一台电脑接收了初始数据。最经济的方法就是，为每一个连通块选择一台代表电脑，向它输入数据。所以，问题的答案就直接转换成了：这个无向图中，总共有多少个独立的连通块？
计算图的连通块数量是图论中的一个基本操作，通常使用 BFS 或 DFS 来实现。用一个 \(vis\) 数组来标记哪些电脑（顶点）已经被访问过（即已经确定属于某个连通块）。从第 1 台电脑开始，遍历到第 \(n\) 台。对于当前遍历到的电脑 \(i\)，如果它还没有被访问过，说明发现了一个新的、尚未探索的连通块。此时，将连通块的数量加一。然后，从这个点 \(i\) 开始进行一次完整的图遍历（BFS 或 DFS），找出所有与 \(i\) 连通的电脑，并将它们全部标记为已访问。
这个算法的复杂度是 \(O(n+m)\)，其中 \(n\) 是电脑数（顶点数），\(m\) 是数据线数（边数）。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
int main()
{
int n, m; // n: 电脑数 (顶点), m: 数据线数 (边)
scanf("%d%d", &n, &m);
// 使用邻接表来存储图的结构
// g[p] 是一个向量，存储所有与电脑p直接相连的电脑
vector<vector<int>> g(n + 1);
for (int i = 1; i <= m; i++) {
int p, q; scanf("%d%d", &p, &q);
// 因为是双向数据线，所以是无向边
// 在p的邻接表中加入q，在q的邻接表中加入p
g[p].push_back(q); g[q].push_back(p);
}
// vis数组用于标记一个电脑是否已经被访问过（即已归属某个连通块）
vector<int> vis(n + 1); // 初始化为0，表示都未访问
int ans = 0; // 存储连通块的数量，即最终答案
// --- 遍历所有电脑，寻找并计算连通块 ---
for (int i = 1; i <= n; i++) {
// 如果当前电脑 i 还没有被访问过
if (!vis[i]) {
// 说明发现了一个新的连通块
ans++; // 连通块数量加一
// --- 从点 i 开始进行广度优先搜索 (BFS) ---
// 目的是找到这个连通块里的所有电脑，并标记它们
queue<int> q;
q.push(i); // 将起点 i 入队
vis[i] = 1; // 标记起点为已访问
while (!q.empty()) {
int u = q.front(); // 取出队首电脑
q.pop();
// 遍历 u 的所有邻居 v
for (int v : g[u]) {
if (!vis[v]) {
vis[v] = 1; // 标记为已访问
q.push(v); // 将其入队，以便后续探索它的邻居
}
}
}
}
}
printf("%d\n", ans);
return 0;
}
习题：P1536 村村通
解题思路
题目要求计算最少需要建设多少条道路，才能使得所有城镇（村庄）都相互连通。“相互连通”意味着整个图变成一个连通图。题目给出的城镇和道路关系，可以看作是一个无向图，其中城镇是节点，道路是边。问题就转化为了：给定一个可能包含多个不相连部分的图，最少需要添加多少条边，才能使整个图变成一个连通图？
假设一个图有 \(k\) 个连通分量，即 \(k\) 个独立的、内部连通但彼此不连通的部分。为了将这 \(k\) 个部分连接起来，最少需要 \(k-1\) 条边。例如，要连接 A, B, C 三个独立的块，只需要两条边即可，比如 A-B 和 B-C，这样 A, B, C 就连通了。因此，本题的核心任务就是计算出图中连通分量的数量 \(k\)，最终答案就是 \(k-1\)。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int N = 1005;
// g: 邻接表，g[i] 存储所有与城镇 i 直接相连的城镇
vector<int> g[N];
// vis: 访问标记数组，vis[i] = true 表示城镇 i 已被访问过
bool vis[N];
int main()
{
// 循环处理多组测试数据
while (true) {
int n; // 城镇数量
scanf("%d", &n);
// 如果读入的 n 为 0，则表示输入结束
if (n == 0) break;
// --- 初始化 ---
// 为下一组测试数据清空状态
for (int i = 1; i <= n; i++) {
g[i].clear(); // 清空邻接表
vis[i] = false; // 重置访问标记
}
int m; // 道路数量
scanf("%d", &m);
// 读取 m 条道路信息，构建邻接表
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
// 道路是双向的，所以是无向图
// 在 x 的邻居列表中加入 y，在 y 的邻居列表中加入 x
g[x].push_back(y); g[y].push_back(x);
}
// --- 计算连通分量数量 ---
int cnt = 0; // 用于统计连通分量的数量
// 遍历所有城镇
for (int i = 1; i <= n; i++) {
// 如果城镇 i 还没有被访问过，说明它属于一个新的、未被发现的连通分量
if (!vis[i]) {
cnt++; // 连通分量数量加一
// 使用广度优先搜索 (BFS) 来找到并标记这个分量中的所有城镇
queue<int> q;
q.push(i); // 将当前城镇作为起点入队
vis[i] = true; // 标记为已访问
while (!q.empty()) {
int u = q.front(); // 取出队首城镇
q.pop();
// 遍历它的所有邻居
for (int v : g[u]) {
// 如果邻居 v 尚未被访问
if (!vis[v]) {
vis[v] = true; // 标记为已访问
q.push(v); // 并将其入队，以便后续处理
}
}
}
}
}
// 最少需要建设的道路数 = 连通分量数 - 1
printf("%d\n", cnt - 1);
}
return 0;
}
例题：P1656 炸铁路
可以将 \(n\) 个城市看作图的顶点（节点），\(m\) 条铁路看作图的无向边。“任意两个城市都可以通过铁路直接或间接到达”，这说明整个图初始时是一个连通图。Key Road 的定义是“有些铁路被毁坏之后，某两个城市无法互相通过铁路到达”。在图论中，如果移除一条边后，原本连通的图变得不再连通（即分裂成两个或更多的连通块），那么这条边就被称为桥或割边。本题目标就是找到这个连通图中的所有“桥”。
最直观、最朴素的方法就是逐一尝试。可以遍历每一条铁路（边），模拟将它“炸毁”（即暂时从图中移除），然后检查剩下的图是否仍然连通。如果图不再连通，那么被移除的这条铁路就是一条“Key Road”（桥）。
遍历每一条边 \(i\)（从 \(1\) 到 \(m\)），在每次循环中，假定第 \(i\) 条边是不存在的。在移除了第 \(i\) 条边的情况下，需要判断整个图是否还连通。一个简单的方法是从任意一个顶点（例如，顶点 \(1\)）开始进行一次图的遍历（DFS 或 BFS），在遍历过程中，要确保不经过被“炸毁”的第 \(i\) 条边。遍历结束后，检查是否所有的 \(n\) 个顶点都被访问到了。如果有任何一个顶点没有被访问到，就说明图已经不再连通，那么第 \(i\) 条边就是一座桥。如果第 \(i\) 条边被确定为桥，就将它记录到一个答案数组中。在检查完所有 \(m\) 条边后，就得到了所有桥的列表。根据题目要求，对找到的桥按照端点编号进行排序，然后输出。
在 DFS 时，为了方便地判断当前要走的边是不是被“禁止”的那条边，可以在邻接表中修改存储的内容，不存储连接的顶点，而是存储对应的边的索引。
整个算法的复杂度是 \(O(m(n+m))\)，因为要对 \(m\) 条边分别进行一次 \(O(n+m)\) 的图遍历，对于本题的数据规模，这个复杂度是可以通过的。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using std::vector;
using std::swap;
using std::sort;
const int N = 155;
const int M = 5005;
// 使用邻接表存储图。g[u]存储与顶点u相连的【边的索引】
vector<int> g[N];
// 定义结构体存储每条铁路（边）
struct Road {
int x, y;
};
Road r[M]; // 存储所有m条铁路
Road ans[M]; // 存储找到的key roads (桥)
bool vis[N]; // 访问数组，用于DFS
/**
* @brief 深度优先搜索，用于检查图的连通性
* @param u 当前访问的城市（顶点）
* @param ban 被“炸毁”的铁路（边）的索引，这条边不可使用
*/
void dfs(int u, int ban) {
vis[u] = true; // 标记当前城市已访问
// 遍历与u相连的所有铁路（边的索引）
for (int i : g[u]) {
// 如果这条铁路就是被禁止的铁路，则跳过
if (i == ban) continue;
// 找到这条铁路的另一个端点 v
int v = r[i].x == u ? r[i].y : r[i].x;
// 如果邻居 v 已经被访问过，则跳过
if (vis[v]) continue;
// 递归地访问 v
dfs(v, ban);
}
}
int main()
{
int n, m; // n: 城市数, m: 铁路数
scanf("%d%d", &n, &m);
// 读取m条铁路并建图
for (int i = 1; i <= m; i++) {
int a, b; scanf("%d%d", &a, &b);
// 保证 a < b，方便后续输出
if (a > b) swap(a, b);
r[i].x = a; r[i].y = b;
// 在邻接表中存储边的索引
g[a].push_back(i);
g[b].push_back(i);
}
int ans_cnt = 0; // 记录找到的key road的数量
// --- 核心逻辑: 暴力枚举每一条铁路，检查其是否为桥 ---
for (int i = 1; i <= m; i++) {
// 每次检查前，重置vis数组
for (int j = 1; j <= n; j++) vis[j] = false;
// 模拟炸毁第i条铁路，然后从城市1开始DFS
dfs(1, i);
// 检查是否所有城市都被访问到
bool ok = true;
for (int j = 1; j <= n; j++)
if (!vis[j]) {
// 如果有城市未被访问，说明图不再连通
ok = false; break;
}
// 如果图不再连通，说明第i条铁路是key road
if (!ok) ans[++ans_cnt] = r[i];
}
// --- 对找到的key roads进行排序 ---
sort(ans + 1, ans + ans_cnt + 1, [](const Road &a, const Road &b) {
if (a.x != b.x) return a.x < b.x; // 首先按x从小到大
return a.y < b.y; // 如果x相同，按y从小到大
});
// --- 输出结果 ---
for (int i = 1; i <= ans_cnt; i++) {
printf("%d %d\n", ans[i].x, ans[i].y);
}
return 0;
}
习题：P3916 图的遍历
解题思路
朴素解法是对每个点 \(i\)（从 \(1\) 到 \(N\)），都进行一次图的遍历（DFS 或 BFS），找出所有能从 \(i\) 到达的点，然后取其中的最大编号作为 \(A(i)\)。每次遍历最坏情况下可能访问 \(O(N)\) 个点和 \(O(M)\) 条边，对所有 \(N\) 个点都执行一次，总复杂度为 \(O(N(N+M))\)，对于 \(N, M\) 高达 \(10^5\) 的数据，这个复杂度太高，无法通过全部测试数据。
朴素解法是“从起点找终点”，效率低下，可以反向思考：对于一个点 \(k\)，有哪些点能够到达它？如果从大到小考虑终点（即从 \(N\) 到 \(1\)），事情就变得清晰了：
- 考虑点 \(N\)：任何能够到达点 \(N\) 的点 \(v\)，其 \(A(v)\) 的值必然是 \(N\)，因为 \(N\) 是所有点中编号最大的，不可能有比它更大的终点。
- 考虑点 \(N-1\)：对于任何能到达 \(N-1\) 的点 \(v\)，如果它不能到达 \(N\)，那么它能到达的最大编号的点就是 \(N-1\)，如果它能到达 \(N\)，那么它的 \(A(v)\) 已经在上一步被确定为 \(N\) 了。
- 推广：当从大到小遍历点 \(i\)（从 \(N\) 到 \(1\)）时，如果一个点 \(v\) 能够到达 \(i\)，并且它不能到达任何比 \(i\) 更大的点，那么就可以确定 \(A(v)=i\)。
如何高效地找出“所有能到达点 \(i\) 的点”？这等价于在反向图上，从点 \(i\) 出发进行遍历，所有能访问到的点，就是在原图中能到达 \(i\) 的点。将原图中所有的有向边 \(u \rightarrow v\) 全部反转，变成 \(v \rightarrow u\)。循环 \(i\) 从 \(N\) 到 \(1\)，在循环中，检查点 \(i\) 是否已经被访问过。
- 如果点 \(i\) 未被访问，说明它无法到达任何比它编号更大的点。因此，它自己能到达的最大点就是它自己，即 \(A(i)=i\)。然后，从点 \(i\) 开始，在反向图上进行一次图遍历。在遍历过程中，所有被访问到的新点 \(v\)，都说明它们在原图中可以到达 \(i\)。因为它们也是首次被访问，所以它们也无法到达比 \(i\) 更大的点。因此，直接确定 \(A(v)=i\)，并将 \(v\) 标记为已访问。
- 如果点 \(i\) 已被访问，说明它在之前的某个 \(k \gt i\) 的步骤中已经被遍历到，这意味着 \(i\) 可以到达一个比它更大的点 \(k\)，\(A(i)\) 已经被正确地设置为了 \(k\)。无需做任何操作，直接跳过。
通过这种方式，每个点和每条边最多只会被访问一次，总时间复杂度为 \(O(N+M)\)，可以通过本题。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
int main()
{
int n, m; scanf("%d%d", &n, &m);
// --- 步骤1: 建立反向图 ---
// 使用邻接表存储图。g[v] 存储的是在原图中指向v的所有节点u
vector<vector<int>> g(n + 1);
for (int i = 1; i <= m; i++) {
int u, v; scanf("%d%d", &u, &v);
// 原本是 u -> v 的边，建成 v -> u
// 这样从 v 出发就能找到所有能到达 v 的点
g[v].push_back(u);
}
// a[i] 存储点i能到达的最大节点编号，即A(i)
// vis[i] 标记点i是否在之前的某个遍历中被访问过
vector<int> vis(n + 1), a(n + 1);
// --- 步骤2 & 3: 从大到小遍历节点，并进行反向图搜索 ---
for (int i = n; i >= 1; i--) {
// 如果点 i 还没有被访问过
if (!vis[i]) {
// 这意味着 i 无法到达任何比它编号更大的点
// 因此，i 能到达的最大点就是它自己
// 从 i 开始，在反向图上进行一次BFS
queue<int> q;
q.push(i);
vis[i] = 1; // 标记 i 为已访问
a[i] = i; // 设置 A(i) = i
while (!q.empty()) {
int u = q.front(); q.pop();
// 遍历所有在原图中指向 u 的点 v
for (int v : g[u]) {
// 如果 v 还没有被访问过
if (!vis[v]) {
// 标记 v 为已访问
vis[v] = 1;
// 将 v 加入队列，继续探索
q.push(v);
// 因为 v 能到达 u，而 u 能到达的最大点是 i
// 且 v 之前未被访问（说明v不能到达比i更大的点）
// 所以 v 能到达的最大点也是 i
a[v] = i;
}
}
}
}
}
// --- 步骤4: 输出结果 ---
for (int i = 1; i <= n; i++) {
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
习题：P2853 [USACO06DEC] Cow Picnic S
解题思路
目标是找到有多少牧场，是所有 \(K\) 只奶牛都能够到达的。牧场可以看作图的顶点（节点），有向路径可以看作图的有向边，这构成了一个有向图。一个牧场 \(P\) 是一个合格的聚餐点，当且仅当，对于每一头奶牛 \(i\)（位于牧场 \(C_i\)），都存在一条从 \(C_i\) 到 \(P\) 的路径。
最直接的想法是，对每一个牧场 \(P\)（从 \(1\) 到 \(N\)），都去检查它是否满足条件。如何检查？对于一个候选牧场 \(P\)，需要验证所有 \(K\) 只奶牛是否都能到达它。这个验证过程本身就需要图的遍历，例如，对于奶牛 \(i\)，可以从它的起点 \(C_i\) 开始进行一次图遍历（DFS 或 BFS），看看能否访问到 \(P\)。这个思路的复杂度（\(O(NK(N+M))\)）太高，无法通过全部测试数据。
朴素思路是“固定终点，遍历起点”，效率低，可以转换一下思路。不问“哪些牧场是所有奶牛都能到达的？”，而是问“对于每个牧场 \(P\)，有多少只奶牛能够到达它？”。如果计算出对于每个牧场 \(P\)，能到达它的奶牛数量，最后只需要统计一下，哪些牧场的这个数量恰好等于 \(K\) 即可。
这个转换后的思路就清晰多了，可以对每一头奶牛进行一次图的遍历。这个算法的时间复杂度是 \(K\) 次图的遍历，即 \(O(K(N+M))\)。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
int main()
{
int k, n, m; // k:奶牛数, n:牧场数(顶点), m:路径数(边)
scanf("%d%d%d", &k, &n, &m);
// 使用邻接表存储有向图的结构
// g[a] 存储所有从牧场a出发可以直接到达的牧场b
vector<vector<int>> g(n + 1);
// c数组存储k只奶牛的起始位置
vector<int> c(k + 1);
for (int i = 1; i <= k; i++) {
scanf("%d", &c[i]);
}
// 读取m条有向边并建图
for (int i = 1; i <= m; i++) {
int a, b; scanf("%d%d", &a, &b);
g[a].push_back(b);
}
// cnt[p] 用于记录能够到达牧场p的奶牛数量
vector<int> cnt(n + 1);
// --- 核心逻辑: 对每只奶牛进行一次图遍历 ---
for (int i = 1; i <= k; i++) {
// 对于每只奶牛，都需要一个独立的vis数组来防止单次BFS中重复访问
vector<int> vis(n + 1);
queue<int> q;
// 从当前奶牛的起点 c[i] 开始BFS
q.push(c[i]);
vis[c[i]] = 1; // 标记起点已访问
cnt[c[i]]++; // 起点本身可以被这只奶牛“到达”，计数加一
while (!q.empty()) {
int u = q.front(); q.pop();
// 遍历 u 能到达的所有邻居 v
for (int v : g[u]) {
// 如果邻居 v 在本次BFS中还未被访问
if (!vis[v]) {
vis[v] = 1; // 标记为已访问
q.push(v); // 入队，以便后续探索
cnt[v]++; // 牧场v的被到达次数加一
}
}
}
}
// --- 统计结果 ---
int ans = 0;
for (int i = 1; i <= n; i++) {
// 如果一个牧场的被到达次数等于奶牛总数k，说明它是合格的聚餐点
if (cnt[i] == k) ans++;
}
printf("%d\n", ans);
return 0;
}
习题：CF1209D Cow and Snacks
解题思路
让难过的人最少，等价于让感到开心（即至少吃到一个点心）的客人数最多。可以将 \(n\) 种点心口味看作 \(n\) 个顶点（节点），每个客人 \(i\) 喜欢口味 \(x_i\) 和 \(y_i\)，这可以看作是一条连接顶点 \(x_i\) 和 \(y_i\) 的无向边。现在，问题变成了：有 \(k\) 条边（代表 \(k\) 个客人），每条边（客人）被“处理”时，会“消耗”掉它的两个端点（点心），要找到一个处理边的顺序，使得尽可能多的边能至少接触到一个未被消耗的端点。
考虑图中的一个连通块，假设这个连通块有 \(V\) 个顶点（点心）和 \(E\) 条边（客人），如果有 \(V\) 个点心，可以满足多少个客人呢？可以从这个连通块中取一棵树出来，安排一个顺序，让客人们沿着这棵树上的边去吃点心。这样，\(V-1\) 个客人可以用 \(V\) 个点心得到满足。那么剩下的客人呢？如果这个连通块有 \(E\) 条边，而这棵树只有 \(V-1\) 条边，那么多出来的 \(E-(V-1)\) 条边就是形成环的“冗余”边，这些边对应的客人，无论怎么安排顺序，当轮到他们时，他们喜欢的两个点心都已经被树上的其他客人吃掉了，因此，这 \(E-(V-1)\) 个客人是必然会难过的。所以，在一个有 \(V\) 个顶点和 \(E\) 条边的连通块中，最少有 \(E-(V-1)\) 个人难过，等价于最多有 \(V-1\) 个人开心。
计算所有连通块中，开心人数的总和。根据输入建立一个无向图，遍历所有顶点（点心），找到图中的所有连通块，这可以用 BFS 或 DFS 实现。对于每一个发现的连通块，计算出它包含的顶点数 \(V\)。在这个连通块中，最多能满足的客人数量是 \(V-1\)。将所有连通块的 \(V-1\) 值加起来，就是整个派对中最多能满足的客人总数。最少难过的客人数就等于总客人数减去这个最多能满足的客人总数。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
int main()
{
int n, k; scanf("%d%d", &n, &k); // n: 点心种类数(顶点), k: 客人数(边)
// 使用邻接表来存储图的结构
// g[x] 存储所有与点心x关联的客人所喜欢的另一种点心
vector<vector<int>> g(n + 1);
for (int i = 1; i <= k; i++) {
int x, y; scanf("%d%d", &x, &y);
// 每个客人对应一条无向边
g[x].push_back(y); g[y].push_back(x);
}
// ans 在这里用于累加所有连通块中，能被满足的最多客人数
int ans = 0;
// vis数组用于标记一个点心(顶点)是否已经被访问过（即已归属某个连通块）
vector<int> vis(n + 1);
// --- 遍历所有顶点，寻找并处理每个连通块 ---
for (int i = 1; i <= n; i++) {
// 如果当前顶点 i 还没有被访问过
if (!vis[i]) {
// 说明发现了一个新的连通块
// --- 从点 i 开始进行广度优先搜索 (BFS) ---
queue<int> q;
q.push(i); // 将起点 i 入队
vis[i] = 1; // 标记起点为已访问
int cnt = 1; // cnt 用于统计当前连通块的顶点数 V
while (!q.empty()) {
int u = q.front(); q.pop();
// 遍历 u 的所有邻居 v
for (int v : g[u]) {
// 如果邻居 v 还没有被访问过
if (!vis[v]) {
vis[v] = 1; // 标记为已访问
q.push(v); // 将其入队
cnt++; // 连通块的顶点数加一
}
}
}
// 在一个有 cnt 个顶点的连通块中，最多能满足 cnt-1 个客人
ans += cnt - 1;
}
}
// 最少难过的人数 = 总客人数 k - 最多能满足的客人数 ans
printf("%d\n", max(0, k - ans));
return 0;
}
习题：P5836 [USACO19DEC] Milk Visits S
解题思路
一个直接的想法是，对于每个查询 \((A,B,C)\)，都从 \(A\) 出发，通过 DFS 或 BFS 找到到 \(B\) 的路径，然后检查路径上所有节点的奶牛类型。这个方法的时间复杂度为 \(O(NM)\)，对于 \(N,M \le 10^5\) 的数据范围来说太慢了，无法通过全部测试数据。
一个朋友不会高兴的唯一情况是：他想喝 \(C\) 类型的牛奶，但从 \(A\) 到 \(B\) 的整条路径上，所有奶牛的类型都不是 \(C\)。换句话说，如果从 \(A\) 到 \(B\) 的路径上，所有奶牛的品质都相同，并且这个品种不是朋友偏好的 \(C\)，那么朋友就不会高兴，在其他情况下，朋友都会高兴。例如，如果朋友想喝 G，但路径上全是 H，他就会不高兴，如果路径上有哪怕一个 G，或者路径上既有 G 又有 H，他都能找到想喝的牛奶，所以会高兴。
基于上述观察，问题的关键变成了判断“从 \(A\) 到 \(B\) 的路径上是否所有奶牛品种都相同”。可以在图上进行遍历来找出由同种奶牛组成的连通块，在遍历过程中，可以给发现的每一个连通块标上不同的编号（染色）。
对于每个查询 \((A,B,C)\)，如果 \(A\) 和 \(B\) 所属的同种奶牛连通块编号相同，说明从 \(A\) 到 \(B\) 是一条完全由同种奶牛组成的路径。检查这种奶牛的品种是否符合朋友的偏好，如果不等于，朋友就不高兴。而除此之外的情况，路径上必然存在符合朋友偏好的奶牛。
这个算法的预处理（建图和染色）时间复杂度是 \(O(N)\)，每个查询的复杂度是 \(O(1)\)，因此总时间复杂度为 \(O(N+M)\)。
参考代码
#include <iostream>
#include <vector>
#include <queue>
#include <string>
using namespace std;
const int N = 100005;
// g: 邻接表，g[i] 存储所有与农场 i 直接相连的农场
vector<int> g[N];
// vis: 访问标记数组，vis[i] = true 表示农场 i 已被访问过
bool vis[N];
// color[i]: 存储农场 i 所属的同种奶牛连通块的编号（颜色）
int color[N];
int main()
{
int n, m; string s;
cin >> n >> m >> s; // 存储奶牛品种的字符串
// --- 建图 ---
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
// 道路是双向的，所以是无向图
g[x].push_back(y); g[y].push_back(x);
}
// --- 使用 BFS 划分并染色同种奶牛的连通块 ---
int cnt = 0; // 用于给不同的连通块分配唯一的编号（颜色）
// 遍历所有农场
for (int i = 1; i <= n; i++) {
// 如果农场 i 还没有被访问过，说明它属于一个新的、未被发现的连通块
if (!vis[i]) {
cnt++; // 发现新连通块，编号+1
// 使用广度优先搜索 (BFS) 来找到并标记这个块中的所有农场
queue<int> q;
q.push(i); vis[i] = true; color[i] = cnt; // 将当前农场染上新的颜色
while (!q.empty()) {
int u = q.front(); q.pop();
// 遍历它的所有邻居
for (int v : g[u]) {
// 关键条件：只有当邻居 v 未被访问过，且奶牛品种与 u 相同时，才将其加入同一个连通块
if (!vis[v] && s[v - 1] == s[u - 1]) { // s是0-indexed, 农场是1-indexed
q.push(v); vis[v] = true; color[v] = cnt; // 将邻居 v 也染上相同的颜色
}
}
}
}
}
// --- 处理 m 个查询 ---
for (int i = 1; i <= m; i++) {
int a, b; char c; cin >> a >> b >> c;
// 判断朋友是否高兴
// 不高兴的唯一条件是：a 和 b 在同一个同种奶牛连通块中（颜色相同）
// 并且这个连通块的奶牛品种不是朋友喜欢的 c
if (color[a] == color[b] && s[a - 1] != c) {
cout << 0; // 不高兴
} else {
cout << 1; // 高兴
}
}
return 0;
}
例题：P1144 最短路计数
解题思路
无权图最短路问题，可以用 BFS 解决。
设 \(ans_u\) 表示 \(1\) 到 \(u\) 的最短路的数量。
if dis[u] + 1 < dis[v]
ans[v] = ans[u]
else
ans[v] += ans[u]
初始化 \(ans_1 = 1\)，认为起点自己到自己，这是一条只有 \(1\) 个点不经过任何边的路。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
const int N = 1000005;
const int MOD = 100003;
std::vector<int> g[N];
int dis[N], ans[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) dis[i] = n;
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
g[x].push_back(y);
g[y].push_back(x);
}
std::queue<int> q;
q.push(1); ans[1] = 1; dis[1] = 0;
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : g[u]) {
if (dis[u] + 1 < dis[v]) {
dis[v] = dis[u] + 1;
q.push(v);
ans[v] = ans[u];
} else if (dis[u] + 1 == dis[v]) {
ans[v] = (ans[v] + ans[u]) % MOD;
}
}
}
for (int i = 1; i <= n; i++) printf("%d\n", ans[i]);
return 0;
}
图论中的树
树的核心定义
在图的大家族中，如果加上一些限制条件，就能得到“树”。
树在图论中的标准定义是：一个连通且无环的无向图。
- 连通：这意味着图中任意两个顶点之间，都至少存在一条路径可以互相到达。整个图是“一体”的，没有孤立的部分。
- 无环：这意味着从图中任意一个点出发，沿着边行走，永远不可能回到这个起点而不重复经过某条边。图中不存在任何“回路”或“圈”。
树的等价性质
除了核心定义，树还有许多非常重要的等价性质。对于一个有 n 个顶点和 m 条边的图，以下说法都是等价的，只要满足其中任意一条，它就是一棵树。
- 该图是连通的且无环的。（这是基本定义）
- 该图中任意两个顶点之间有且仅有一条简单路径。
- “有”路径保证了连通性。
- “仅有一条”路径保持了无环性（如果存在两条不同路径，它们必然会构成一个环）。
- 该图是连通的，并且边的数量 m = n - 1。因为 n-1 是连接 n 个顶点所需的最少边数，再少一条边，图就会断开。
- 该图是无环的，并且边的数量 m = n - 1。对于一个无环图，n-1 是它能拥有最多边数，再多一条边，必然会形成一个环。
- 该图是极小连通图。即图是连通的，但移除任意一条边都会导致图不再连通，这说明图中没有任何“冗余”的边（即环）。
- 该图是极大无环图。即图是无环的，但添加任意一条边（连接两个已存在的顶点）都会形成一个环。
这些性质从不同角度描述了树的本质：它是一种用最少的边来保持所有顶点连通的结构。
不定项选择题：下列说法中，是树的性质的有？
- A. 无环
- B. 任意两个节点之间有且只有一条简单路径
- C. 有且只有一个简单环
- D. 边的数目恰是顶点数目减 1
答案
ABD。
习题：P8971 『GROI-R1』 虹色的彼岸花
解题思路
计算有多少种给每个点赋权值的方法，满足给定的约束条件。
- 所有点的点权 \(p_i\) 必须在 \([l,r]\) 范围内。
- 对于有点权的边 \((u,v)\)，其权值为 \(w\)，必须满足 \(p_u + p_v = w\)。
- 没有边权的边，对点权没有限制。
没有边权的边，实际上是分成了若干个独立的连通块，每个连通块的点权方案数可以独立计算，最终的总方案数是所有连通块方案数的乘积。在一个由带权边连接的连通块中，只要任意一个点的点权被确定，那么所有其他点的点权也随之被唯一确定，例如，如果知道了点 \(u\) 的点权 \(p_u\)，那么与它相连的 \(p_v\) 就等于 \(w-p_u\)，与 \(v\) 相连的 \(p_z\) 就等于 \(w' - p_v\)，以此类推。
基于上述观察，可以对每个连通块，选择一个基准点（例如，DFS 时遇到的第一个点），假设它的点权为 \(x\)。然后，可以通过 DFS 遍历整个连通块，用 \(x\) 来表示出所有其他点的点权。如何表示？假设从基准点 \(u\) 开始 DFS，设 \(p_u = x\)。当从 \(u\) 走到邻居 \(v\)，边权为 \(w\) 时，有 \(p_u + p_v = w\)，所以 \(p_v = w - p_u\)。通过这个关系，可以发现，连通块中任意一个点 \(v\) 的点权 \(p_v\) 都可以表示成 \(kx+b\) 的形式，其中 \(k\) 只能是 \(+1\) 或 \(-1\)，\(b\) 是一个由边权累加/减得到的常数。具体来说，如果 \(v\) 与基准点 \(u\) 的距离是偶数，那么 \(p_v = x + b_v\)（\(k=1\)），如果距离是奇数，那么 \(p_v = -x + b_v\)（\(k=-1\)）。
现在，所有点的点权都用基准点 \(u\) 的点权 \(x\) 表示出来了。原来的约束 \(l \le p_v \le r\) 就变成了对 \(x\) 的约束：\(l \le kx+b_v \le r\)。可以解出这个关于 \(x\) 的不等式，如果 \(k=1\)（\(p_v = x + b_v\)），则 \(l - b_v \le x \le r - b_v\)；如果 \(k=-1\)（\(p_v = -x + b_v\)），则 \(l \le -x + b_v \le r\)，变形后得到 \(b_v - r \le x \le b_v - l\)。每个点 \(x\) 都会给 \(x\) 带来一个约束区间，\(x\) 必须满足所有这些约束，因此 \(x\) 的最终可行范围是所有这些约束区间的交集。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using ll = long long;
using std::vector;
using std::max;
using std::min;
const int N = 200005;
const int MOD = 1000000007;
// 边结构体
struct Edge {
int to, w;
};
vector<Edge> tr[N]; // 邻接表存储
bool vis[N]; // 访问数组，标记节点是否已属于某个处理过的连通块
ll nowl, nowr, l, r; // l,r: 题目给定的全局范围; nowl,nowr: 当前连通块中基准点x的可行范围
/**
* @brief DFS遍历一个连通块，并将所有节点的约束统一到基准点x上
* @param u 当前节点
* @param k 当前节点点权p_u = k*x + b 中的 k (+1或-1)
* @param b 当前节点点权p_u = k*x + b 中的 b (常数偏移)
*/
void dfs(int u, int k, ll b) {
vis[u] = true; // 标记u已访问
// 根据 p_u 的约束 l <= p_u <= r，反解出对基准点x的约束
if (k > 0) { // p_u = x + b => l-b <= x <= r-b
nowl = max(nowl, l - b);
nowr = min(nowr, r - b);
} else { // p_u = -x + b => b-r <= x <= b-l
nowl = max(nowl, b - r);
nowr = min(nowr, b - l);
}
// 递归访问邻居
for (Edge e : tr[u]) {
int v = e.to, w = e.w;
if (vis[v]) continue;
// p_v = w - p_u = w - (k*x + b) = (-k)*x + (w - b)
// 所以下一个节点的k'=-k, b'=w-b
dfs(v, -k, w - b);
}
}
void solve() {
int n; scanf("%d%lld%lld", &n, &l, &r);
// 初始化
for (int i = 1; i <= n; i++) {
vis[i] = false; tr[i].clear();
}
// 建图，只建立有边权的边
for (int i = 1; i < n; i++) {
int op, u, v; scanf("%d%d%d", &op, &u, &v);
if (op == 1) {
int w; scanf("%d", &w);
tr[u].push_back({v, w});
tr[v].push_back({u, w});
}
}
int ans = 1; // 最终答案，初始化为1（乘法单位元）
// 遍历所有节点，处理每个连通块
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
// 发现一个新的连通块
// 初始化该连通块的基准点x的可行范围为全局范围
nowl = l; nowr = r;
// 从i开始DFS，i是基准点，p_i = 1*x + 0
dfs(i, 1, 0);
// 如果可行范围无效，则总方案数为0
if (nowl > nowr) {
ans = 0; break;
}
// 否则，将该连通块的方案数（即x的可取值个数）累乘到总答案
ans = 1ll * ans * (nowr - nowl + 1) % MOD;
}
}
printf("%d\n", ans);
}
int main()
{
int t; scanf("%d", &t);
for (int i = 1; i <= t; i++) solve();
return 0;
}
三色标记法
在标准的 DFS 中，通常用一个数组来记录节点是否被访问过（两种状态：访问/未访问）。但在有向图中，这两种状态不足以区分“当前路径上的节点”和“之前其他路径访问过的节点”。
三色标记法通过为每个节点分配三种颜色（状态）来解决问题：
- 白色：代表节点从未被访问过，这是所有节点的初始状态。
- 灰色：代表节点正在被访问，一个节点从首次进入其
dfs函数开始，到其所有邻居节点都被探索完毕为止，都处于灰色状态，所有灰色节点共同构成了当前正在探索的路径，也就是当前的递归调用栈。 - 黑色：代表节点已经访问完毕，当一个节点的所有邻居（及其所有后代）都已被完全访问后，该节点变为黑色，这表示已经完成了对该节点的所有探索，并即将从其
dfs函数返回。
三色标记法的威力在于它能精确地识别出图中的返祖边，而返祖边的存在正是图中存在环的充要条件。
其核心判断逻辑非常简洁：
如果在 DFS 过程中，从一个灰色节点 \(u\) 出发，试图访问的邻居节点 \(v\) 也是灰色，那么就证明图中存在一个环。
为什么？因为节点 \(v\) 是灰色的，意味着它也在当前的递归调用栈上，也就是说 \(v\) 是 \(u\) 的一个祖先节点，现在又发现了一条从 \(u\) 指向 \(v\) 的边，这条边就构成了一个从祖先 \(v\) 出发，经过一系列节点到达 \(u\)，最后又回到 \(v\) 的闭合路径，即“环”。
根据目标节点颜色的不同，可以判断边的类型：
- 灰色节点 \(u\) 指向白色节点 \(v\)：树边，这是正常的 DFS 探索路径，将递归访问 \(v\)。
- 灰色节点 \(u\) 指向灰色节点 \(v\)：返祖边，\(v\) 是 \(u\) 的祖先，检测到环。
- 灰色节点 \(u\) 指向黑色节点 \(v\)：前向边或交叉边，\(v\) 已经被完全探索完毕，它不是当前路径的祖先，因此不会构成环，忽略即可。
习题：P2661 [NOIP 2015 提高组] 信息传递
解题思路
可以将 \(n\) 个同学看作 \(n\) 个顶点（节点），信息传递关系 \(i \rightarrow T_i\) 可以看作一条从顶点 \(i\) 指向顶点 \(T_i\) 的有向边。“当有人从别人口中得知自己的生日时，游戏结束”，这在图论模型中意味着，信息从某个节点 \(A\) 出发，沿着边传递，经过 \(k\) 轮后，又回到了节点 \(A\)，这恰好是图中一个长度为 \(k\) 的有向环的定义。游戏在第一次有人得知自己生日时就结束，因此，最终目标就是找到这个图中所有有向环里，长度最小的那个环，这个最小环的长度，就是游戏进行的轮数。
可以使用三色标记法找出所有的环，为了计算环的长度，需要在 DFS 时记录下每个节点被访问时的“深度”或“步数”。在 DFS 过程中，可以将每个点 \(u\) 是从当前 DFS 起点开始的深度存入 \(num_u\)。当从节点 \(u\) 访问 \(v\) 时，如果发现 \(v\) 是灰色，假设当前深度是 \(depth\)，那么环的长度就是 \(depth - num_v + 1\)。
参考代码
#include <cstdio>
#include <vector>
using namespace std;
// t: 存储信息传递对象，t[i] = T_i
// vis: 三色标记数组 (0:未访问, 1:正在访问/在当前路径上, 2:已访问完毕)
// num: 记录节点在当前DFS路径中的深度
vector<int> t, vis, num;
int ans; // 全局变量，存储找到的最小环长度
/**
* @brief 使用三色标记DFS寻找最小环
* @param u 当前节点
* @param depth 当前DFS的深度
*/
void dfs(int u, int depth) {
// 将当前节点u标记为“正在访问”(灰色)，并记录其深度
vis[u] = 1; num[u] = depth;
int next_node = t[u]; // 获取下一个节点
// 如果下一个节点是“正在访问”(灰色)
if (vis[next_node] == 1) {
// 找到了一个环！
// 环的长度 = 当前深度 - 环入口节点的深度 + 1
ans = min(ans, depth - num[next_node] + 1);
} else if (vis[next_node] == 0) { // 如果下一个节点是“未访问”(白色)
// 继续向下递归探索
dfs(next_node, depth + 1);
}
// 如果下一个节点是“已访问完毕”(黑色)，则什么都不做，直接回溯。
// 节点u的所有路径都已探索完毕，将其标记为“已访问完毕”(黑色)
vis[u] = 2;
}
int main()
{
int n; scanf("%d", &n);
// 初始化容器大小，vis初始全为0(白色)
t.resize(n + 1); vis.resize(n + 1); num.resize(n + 1);
for (int i = 1; i <= n; i++) {
scanf("%d", &t[i]);
}
// 初始化最小环长为一个足够大的值
ans = n;
for (int i = 1; i <= n; i++) {
if (vis[i] == 0) {
dfs(i, 1);
}
}
printf("%d\n", ans);
return 0;
}
欧拉图
故事起源：哥尼斯堡七桥问题
这个概念源于一个 18 世纪的著名数学问题——哥尼斯堡七桥问题。
在当时的普鲁士哥尼斯堡市（现在的俄罗斯加里宁格勒），有一条河穿流而过，河中有两个小岛。城市、小岛之间由七座桥梁连接起来，如下图所示。
当地居民中流传着一个难题：一个人能否从任意一点出发，走遍这七座桥，每座桥只走一次，最后回到起点？
无数人尝试都失败了。直到 1736 年，伟大的数学家莱昂哈德·欧拉（Leonhard Euler）解决了这个问题。他没有亲自去走，而是将这个问题抽象成了一个数学模型，从而开创了图论的先河。
欧拉的抽象方法
- 他将陆地（河的两岸河两个岛）看做是顶点，总共 4 个顶点。
- 他将连接陆地的桥梁看做是边，总共 7 条边。
这样，现实世界的地图就变成了一个简单的图。
现在，问题就转化为：能否在这个图中找到一条路径，经过每一条边恰好一次，并最终回到起点？
核心定义
基于上述问题，引出欧拉图相关的几个核心定义：
- 欧拉路径：在一个图中，如果存在一条路径，能够经过图中每一条边，且每条边只经过一次，那么这条路径就叫作“欧拉路径”。这就像小时候玩的“一笔画”问题，起点和终点可以不一样。
- 欧拉回路：如果一条欧拉路径的起点和终点是同一个顶点，那么它就是一个“欧拉回路”。哥尼斯堡七桥问题问的就是是否存在“欧拉回路”。
- 欧拉图：一个含有欧拉回路的图就被称为“欧拉图”。
- 半欧拉图：一个只含有欧拉路径但不含有欧拉回路的图，被称为“半欧拉图”。
如何判断一个图是不是欧拉图？
欧拉不仅提出了问题，还给出了完美的判定方法。这个方法的核心在于顶点的度。
顶点的度：连接到一个顶点的边的数量。
- 如果一个顶点的度是偶数，我们称之为偶度顶点。
- 如果一个顶点的度是奇数，我们称之为奇度顶点。
欧拉定理
- 判断欧拉回路（即判断是否为欧拉图）：一个连通图（图中任意两点都可达）是欧拉图的充要条件是图中所有顶点的度都是偶数。
- 直观理解：想象一下，除了起点和终点，任何一个“中途”的顶点，你从一条边“进入”这个点，就必须从另一条边“离开”。这样有进有出，成双成对，所以它连接的边必然是偶数条。对于起点/终点来说，第一次“离开”和最后一次“回来”，也构成了一对，所以也必须是偶数。
- 判断欧拉路径（即判断是否为半欧拉图）：一个连通图是半欧拉图的充要条件是图中恰好有两个顶点的度是奇数。
- 直观理解：这两个奇度顶点必定是“一笔画”的起点和终点。起点只出不进（第一次），终点只进不出（最后一次），而中间的所有点依然是有进有出，所以必须是偶度顶点。
解决哥尼斯堡七桥问题
现在回头看七桥问题。将四个顶点的度计算一下：
- 北岸：3 度（连接 3 座桥）
- 南岸：3 度（连接 3 座桥）
- 左岛：5 度（连接 5 座桥）
- 右岛：3 度（连接 3 座桥）
这个图有四个奇度顶点。
- 它不满足“所有顶点都是偶度”，所以它不是欧拉图，不存在欧拉回路。
- 它也不满足“恰好有两个奇度顶点”，所以它也不是半欧拉图，连欧拉路径都不存在。
结论：欧拉因此断定，哥尼斯堡的居民永远无法完成这个挑战。
选择题：假设有一个包含 \(n\) 个顶点的无向图，且该图是欧拉图。以下关于该图的描述中哪一项不一定正确？
- A. 所有顶点的度数均为偶数
- B. 该图连通
- C. 该图存在一个欧拉回路
- D. 该图的边数是奇数
答案
D。欧拉图的边数可以是奇数，也可以是偶数。
例如一个最简单的正方形图，4 个顶点，4 条边，是一个欧拉图；一个三角形图，3 个顶点，3 条边，也是一个欧拉图。
选择题：每个顶点度数均为 2 的无向图称为“2 正规图”。由编号从 1 到 n 的顶点构成的所有 2 正规图，其中包含欧拉回路的不同 2 正规图的数量为？
- A. \(n!\)
- B. \((n-1)!\)
- C. \(n!/2\)
- D. \((n-1)!/2\)
答案
符合条件的 2 正规图实际上就是 \(n\) 元环，先随便分配 \(n\) 个节点编号，方案数为 \(n!\)，但是环有“旋转对称性”，所以要除以 \(n\)，无向图还有“翻转对称性”，还要除以 2，因此答案为 D。
平面图
想象一下，在一张无限大的白纸上画一个图，如果存在一种画法，能够使得图中的所有边除了在顶点处之外，互不交叉，那么这个图就称为平面图。
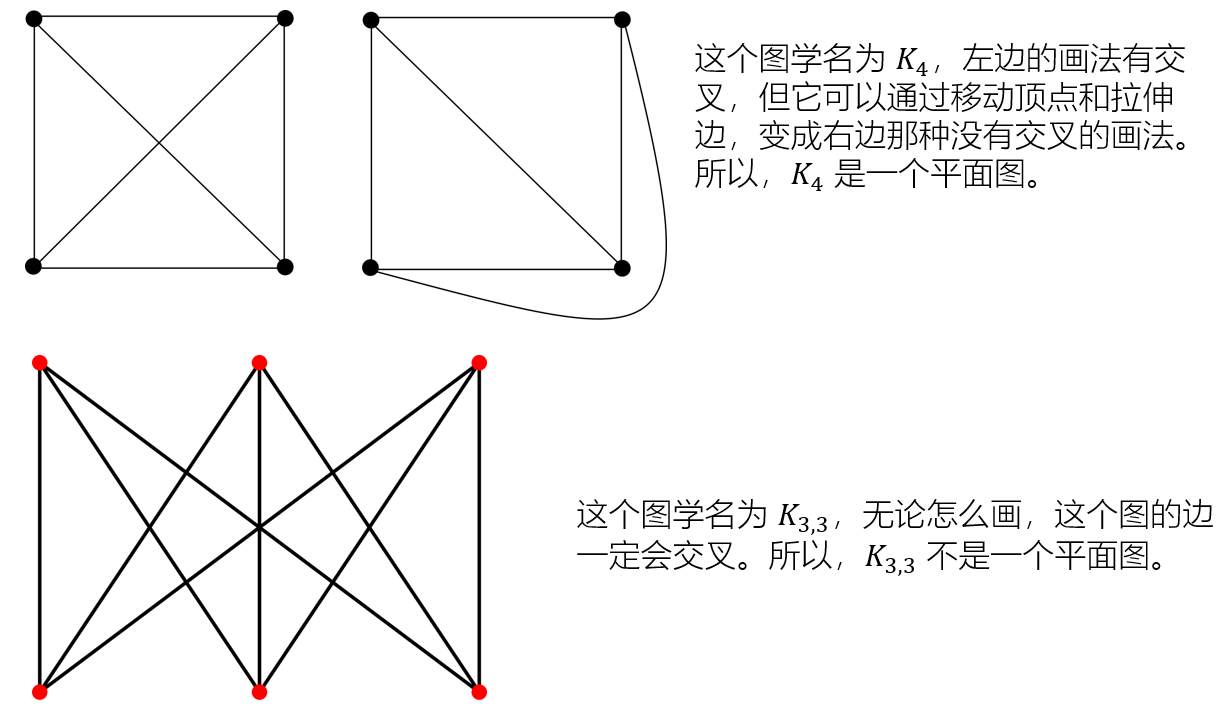
平面图有一些非常优美的数学性质，其中最核心的是欧拉公式：对于任何一个连通的平面图，其顶点数 \(V\)、边数 \(E\) 和面数 \(F\) 之间满足一个恒定的关系：\(V - E + F = 2\)。
证明
证明方法：对图的边数 \(E\) 使用数学归纳法。
从最简单的连通图开始，当边数 \(E = 0\) 时，为了保持图的连通性，图中必然只有一个顶点。
- 此时，\(V = 1\)，\(E = 0\)。
- 这个孤立的点将整个平面看作一个区域，所以面数 \(F = 1\)。
- 将这些值代入欧拉公式，\(V - E + F = 1 - 0 + 1 = 2\)，成立。
假设对于任何边数 \(E'\) 满足 \(0 \le E' \lt E\) 的连通平面图，欧拉公式 \(V' - E' + F' = 2\) 都成立。
现在，来证明当图 \(G\) 的边数为 \(E \ (E \gt 0)\) 时，公式也成立。从图 \(G\) 中去掉一条边 \(e\)，得到一个新的图 \(G'\)。\(G'\) 的边数是 \(E-1\)，根据归纳假设，欧拉公式对 \(G'\) 也成立。
需要分两种情况来讨论去掉边 \(e\) 的后果。
情况一：图 \(G\) 含有圈
如果图 \(G\) 不是一棵树，那么它必然包含至少一个圈，可以从任意一个圈上选择一条边 \(e\) 并移除它。
- 移除边 \(e\) 的影响
- 顶点数 \(V\) 保持不变，即 \(V' = V\)
- 边数 \(E\) 减少了 1，即 \(E' = E - 1\)
- 一条圈上的边一定是两个相邻面的分界线，当这条边 \(e\) 被移除后，这两个相邻的面会合并成一个面。就像拆掉两个房间之间的一堵墙，两个房间就变成了一个大房间。所以，面数也减少了 1，即 \(F' = F - 1\)。
- 应用归纳假设：对于新图 \(G'\)，有 \(V' - E' + F' = 2\)。，有 \(V - E + F = V' - (E' + 1) + (F' + 1) = V' - E' - 1 + F' + 1 = V' - E' + F' = 2\)。所以，在这种情况下，公式对图 \(G\) 成立。
情况二：图 \(G\) 不含圈（即 \(G\) 是一棵树）
如果一个连通图不含圈，那么它一定是一棵树。
- 树的性质
- 对于任何一棵树，其边数 \(E\) 和顶点数 \(V\) 之间有固定的关系：\(E = V - 1\)。
- 将一棵树画在平面上，由于它没有任何圈，它无法围成任何有界区域。因此，树只有一个面，就是它所在的整个平面（无界区域），所以 \(F = 1\)。
- 将树的这两个性质直接代入欧拉公式的左边：\(V - E + F = V - (V - 1) + 1 = 2\)。所以，对于任何树，欧拉公式都直接成立。
根据数学归纳法原理，欧拉公式 \(V-E+F=2\) 对所有连通平面图都成立。
欧拉公式可以产生一个推论：对于任何 \(V \ge 3\) 的简单连通平面图，必然满足 \(E \le 3V-6\)。
为什么？因为在平面图中，每个面至少由 3 条边围成，而每条边最多属于 2 个面，所以 \(3F \le 2E\)，将欧拉公式 \(F = 2 - V + E\) 代入即可得到此结论。
应用：可以用它来证明完全图 \(K_5\)（5 个顶点，任意两点间都有边）不是平面图。
- \(K_5\) 中，\(V = 5\)，\(E = 10\)。
- 根据推论，\(E\) 必须小于等于 \(3 \times 5 - 6 = 9\)。
- 但 \(K_5\) 的边数是 10，而 \(10 \gt 9\)，所以 \(K_5\) 不可能是平面图。
平面图不只在于数学理论，它在现实世界中有广泛的应用：
- 电路设计布局：设计印刷电路板时，目标是在一个二维平面上布置元器件和导线，导线不能交叉（除非使用多层板，但层数越少成本越低）。判断一个电路图能否在单层板上实现，本质上就是一个平面图判定问题。
- 地图绘制与四色定理：任何一张地图都可以表示为一个平面图（国家是顶点，相邻关系是边），著名的“四色定理”（任何地图只需要四种颜色就能保证相邻区域颜色不同）就是一个关于平面图的著名结论。
- 网络可视化：在绘制复杂的网络图（如社交网络、计算机网络）时，为了让图形清晰易读，算法会尽量减少边的交叉，这背后就运用了平面图的理论。
- 设施规划：在城市或建筑内规划管道、线路等，要避免交叉，也与平面图的布局思想有关。
双连通图
对于无向图 \(G = (V,E)\)，如果在删去某个顶点 \(u\) 及其关联的边后，\(G\) 的连通分量数量增多，则称 \(u\) 为图 \(G\) 的割点；如果删去某条边 \(e\) 但保留其关联顶点后，\(G\) 的连通分量数量增多，则称 \(e\) 是图 \(G\) 的割边或桥。
不存在割点的无向图称为 2-连通图，也成为点双连通图或重连通图，\(G\) 的极大 2-连通子图称为 \(G\) 的 2-连通分量。一个无向图是重连通的，当且仅当图中任意两个顶点之间至少有两条路径，且这两条路径除起点、终点外不含其它公共顶点。
不存在割边的无向图称为 2-边连通图，也称为边双连通图，\(G\) 的极大 2-边连通子图称为 \(G\) 的 2-边连通分量。
强连通图
在有向图中，如果对于图中任意两个不同的顶点 A 和 B，都同时存在从 A 到 B 的路径和从 B 到 A 的路径，那么这个有向图就被称为强连通图，强连通图是衡量有向图连通性的概念。
强连通分量就是一个有向图中的极大强连通子图。
选择题：强连通图的性质不包括？
- A. 每个顶点的度数至少为 1
- B. 任意两个顶点之间都有边相连
- C. 任意两个顶点之间都有路径相连
- D. 每个顶点至少都连有一条边
答案
正确答案是 B。
强连通图的关键在于路径可达性，而不是边的直接连接。
浙公网安备 33010602011771号