最小生成树
最小生成树是有边权的无向图中的一个常见问题。
在无向图 G(V,E) 中,把连通而且不含有环路的一个子图称为一棵生成树,它包含全部 n 个点和 n-1 条边。边权之和最小的树称为最小生成树(Minimal Spanning Tree, MST)。
MST 的计算用到了一个基本性质:一个图的 MST 一定包含图中权值最小的边。这使得可以用贪心法构造 MST,因为 MST 问题满足贪心法的“最优性原理”,即全局最优包含局部最优。
图的两个基本元素是点和边,与此对应,有两种算法可以构造 MST,这两种算法都基于贪心法。
例题:P3366 【模板】最小生成树
现有一张 n 个点 m 条边的无向图,求其最小生成树边权之和;如果图不连通则输出
orz。
输入格式: 第一行包含两个整数 n,m。接下来 m 行每行三个整数 \(x_i,y_i,z_i\),表示存在一条从 \(x_i\) 到 \(y_i\) 的无向边,边权为 \(z_i\)。
输出格式: 一行一个整数,表示最小生成树边权之和;如果图不连通则输出orz。
数据范围:\(1 \le n \le 5 \times 10^3, 1 \le m \le 2 \times 10^5, 1 \le z \le 10^4\)。
解法 1(Prim 算法): 不妨先假设图连通。由于所有点最后都会在最小生成树中,所以不妨任意设置一个起点(这里设为 \(1\))。该算法的大体思路是从点 \(1\) 开始通过贪心不断向外扩展当前的树,直到所有点都进入生成树中。用一个 dis 数组来记录到目前为止当前树中的点到其他点的最短边长。
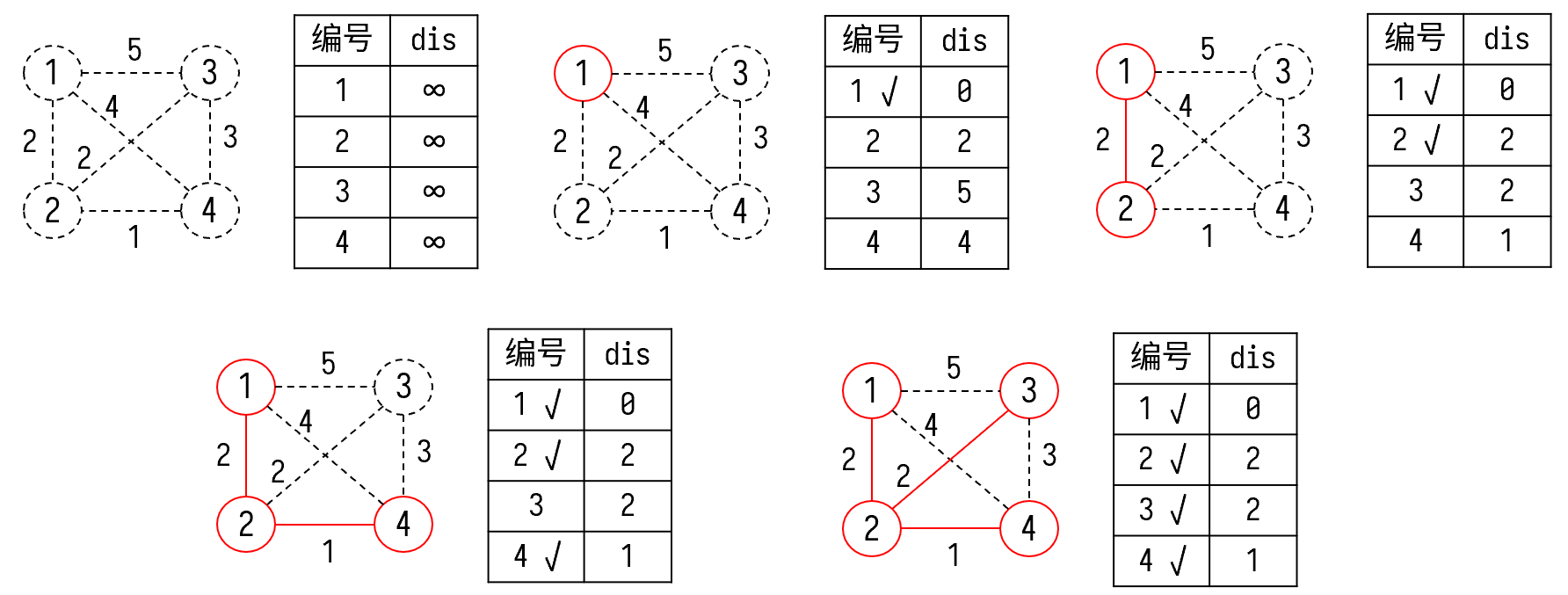
- 在初始状态下,先将整个 dis 数组设为 ∞,表示未更新。
- 先将 1 号点放入生成树中并打上标记。此时当前的树中只有一个点,没有边。接着通过 1 号点来更新 dis 数组。这里有一个结论:任何时刻,未标记的点中 dis 最小者,其 dis 值所对应的边一定在一棵最小生成树中。
- 容易发现,此时 2 号点的 dis 值是没有标记的点中最小的。根据结论,2 号点的 dis 值所对应的边(即 1 到 2 的边)一定在最小生成树中。将 2 打上标记并用与 2 号点相连的边来更新 dis 数组。
- 此时 4 号点的 dis 值是没有标记的点中最小的。根据结论,4 号点的 dis 值所对应的边(即 2 到 4 的边)一定在最小生成树中。此时,将 4 号点放进最小生成树(打上标记),并用与其相连的边来更新 dis 数组。
- 最后,剩余 3 号点一个点。根据结论,3 号点 dis 的值所对应的边(即 2 到 3 的边)一定在最小生成树中。将 3 号点放入最小生成树中并打上标记,程序结束。
在求最小生成树的同时累加生成树各边的边权,可以得到答案为 5。
结论: 任何时刻,未标记的点中 dis 最小者,其 dis 值所对应的边(设为 \(e_1\))一定在一棵最小生成树中。
证明: 可以采用反证法。假设最小生成树已经建完,此时再将 \(e_1\) 边加入最小生成树中,则树中出现了一个环。由于这条边连接的是一个已标记的点与未标记的点,则环中显然还有一条边 \(e_2\) 也是连接一个已标记的点与一个未标记的点。此时用 \(e_1\) 对 \(e_2\) 进行替换,得到的结果一定更优。
如果此时的 \(e_1\) 边权和 \(e_2\) 相等,那将 \(e_1\) 和 \(e_2\) 替换同样是一棵最小生成树。对于这种情况两条边可以任选一条放入最小生成树,对答案没有影响。这也印证了题目中最小生成树可能不止一棵的说法。
这种求最小生成树的方法是 Prim 算法,其过程概括如下:
- 将 1 号点加入当前生成树中并打上标记,同时更新 dis 数组;
- 选择所有未标记的点中 dis 最小的点;
- 将该点加入当前生成树中并打上标记;
- 使用与该点相连的所有连边更新 dis 数组;
- 重复第 2 到第 4 步,直到所有点都已经被标记或所有未标记的点都不存在连边与已标记的点直接相连。
需要注意的是,如果出现所有未标记的点都不存在连边与已标记的点直接相连的情况就意味着图不连通。此时也应当结束算法。可以再记录一个变量 cnt,代表打上标记的点的数量。如果最后 \(cnt \ne n\),则可以判定无解。参考代码如下:
#include <cstdio>
#include <vector>
#include <utility>
using namespace std;
typedef pair<int, int> PII;
const int N = 5005;
const int INF = 1e9;
vector<PII> graph[N]; // <y, z>
bool vis[N];
int dis[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int x, y, z; scanf("%d%d%d", &x, &y, &z);
graph[x].push_back({y, z});
graph[y].push_back({x, z});
}
for (int i = 0; i <= n; i++) dis[i] = INF; // 初始化dis数组
dis[1] = 0;
int cnt = 0, ans = 0;
while (true) {
int u = 0;
for (int i = 1; i <= n; i++) // 寻找dis最小的点
if (!vis[i] && dis[i] < dis[u]) u = i;
if (u == 0) break;
vis[u] = true; cnt++; ans += dis[u]; // 将边加入生成树并将点标记
for (PII e : graph[u]) {
int v = e.first, w = e.second;
if (w < dis[v]) dis[v] = w; // 更新dis数组
}
}
if (cnt < n) printf("orz\n");
else printf("%d\n", ans);
return 0;
}
容易分析得出这段程序的时间复杂度为 \(O(n^2+m)\),在本题中可以通过。但如果 \(n\) 较大则可能出现超时的情况。
可以用一个堆来优化,每次更新 dis 数组后将 dis 值与对应点存入一个优先队列,依据 dis 值排序。这样就可以将时间复杂度优化到 \(O(m \log m)\)。
#include <cstdio>
#include <vector>
#include <utility>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 5005;
const int INF = 1e9;
vector<PII> graph[N]; // <y,z>
bool vis[N];
int dis[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int x, y, z; scanf("%d%d%d", &x, &y, &z);
graph[x].push_back({y, z});
graph[y].push_back({x, z});
}
for (int i = 1; i <= n; i++) dis[i] = INF;
// 用于寻找dis最小的点的优先队列
priority_queue<PII, vector<PII>, greater<PII>> q; // <weight, node_id>
q.push({0, 1}); dis[1] = 0;
int cnt = 0, ans = 0;
while (!q.empty()) {
PII cur = q.top(); q.pop(); // 取出dis最小的点
int u = cur.second;
if (vis[u]) continue; // 如果已经标记过就跳过
vis[u] = true; cnt++; ans += dis[u];
for (PII e : graph[u]) {
int v = e.first, w = e.second;
if (w < dis[v]) {
dis[v] = w; q.push({w, v}); // 更新成功后更新优先队列
}
}
}
if (cnt < n) printf("orz\n");
else printf("%d\n", ans);
return 0;
}
解法 2(Kruskal 算法): 同样地,不妨假设图连通。该算法的大体思路是直接对边进行排序,然后从小到大进行合并。可以想象,在程序运行的过程中将会出现很多的连通块,并且连通块的数量会越来越小。在最后它们会合并为同一个连通块,即最终的最小生成树。
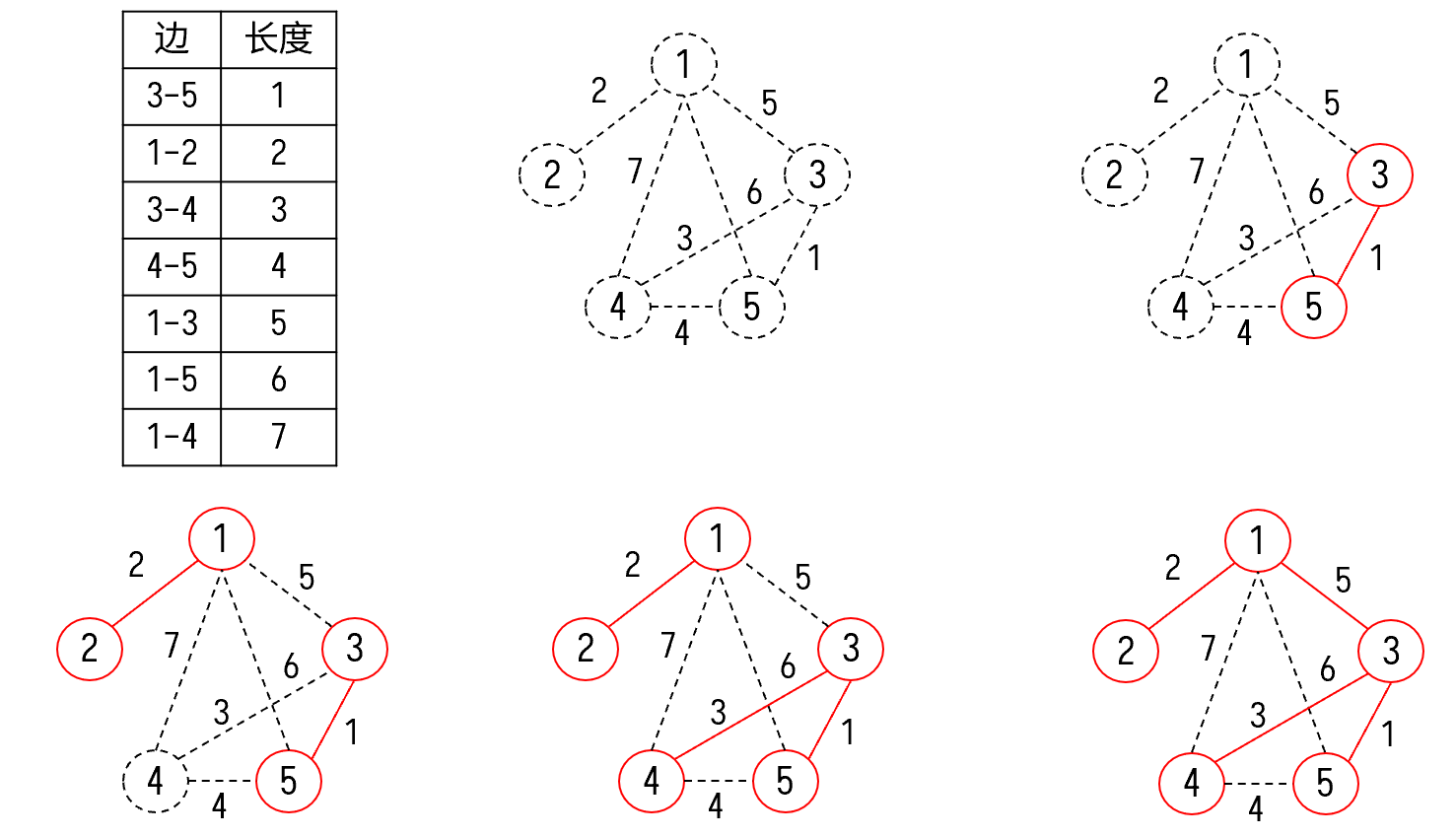
- 最开始时,所有的点和边都没有被选中。这里同样有一个结论,任何时刻,所有未使用的边中边权最小的一条,如果它所连接的两个点不在同一个连通块中,则这条边一定在最小生成树中。此时,将所有的边按照长度从小到大排序。
- 选择目前所有边中边权最小的一条(即 3 到 5 的边)。由于 3 和 5 目前不在同一个连通块中,根据结论,这条边一定在一棵最小生成树中。
- 类似地,接下来枚举到 1 和 2 的连边,以及 3 和 4 的连边。根据结论,这两条边也在最小生成树中。
- 接下来枚举到的是 4 和 5 的连边。然而此时发现,4 和 5 已经连通,所以这条边不在最小生成树中,可以直接将它舍弃。
- 最后,枚举到连接 1 和 3 的连边。将这条边加入最小生成树,发现整张图已经连通。
结论: 所有未使用的边中边权最小的一条(设为 \(e_1\)),如果它所连接的两个点不在同一个连通块中,则这条边已经在一棵最小生成树中。
证明: 类似于 Prim 算法的证明,假设最小生成树已经建完,此时再将 \(e_1\) 边加入最小生成树中,则树中出现了一个环。由于这条边连接的是两个未连通的点,则环中显然还有一条边 \(e_2\) 也未被标记,显然 \(e_1\) 替换 \(e_2\) 更优。同理,若 \(e_1\) 与 \(e_2\) 边权相同,则互相替换不影响答案。
对于连通块的记录,可以使用一个并查集进行处理。最初每个点自成一个集合,每当一条边加入生成树时就合并其所连接的两个点所属的集合即可。对于无解的判断,只需要判断合并的次数是否为 \(n-1\) 次即可。
这种求最小生成树的算法是 Kruskal 算法,其过程概括如下:
- 将所有的边从小到大排序;
- 将所有点分别放入各自的并查集中;
- 选择所有未使用的边中边权最小的;
- 若该边所连接的两个点已经连通,则舍去,否则合并这两个并查集;
- 重复第 3 到 4 步,直到所有点都已经被标记或所有未标记的点都不存在连边与已标记的点直接相连。
因为 Kruskal 算法的瓶颈在于将所有的边排序,所以时间复杂度为 \(O(m \log m)\)。
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5005;
const int M = 200005;
struct Edge {
int x, y, z;
bool operator<(const Edge& other) const {
return z < other.z;
}
};
Edge e[M];
int fa[N];
int query(int x) {
return fa[x] == x ? x : fa[x] = query(fa[x]); // 并查集查询(路径压缩)
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= m; i++) scanf("%d%d%d", &e[i].x, &e[i].y, &e[i].z);
sort(e + 1, e + m + 1); // 将边排序
int ans = 0, cnt = 0;
for (int i = 1; i <= m; i++) {
int qx = query(e[i].x), qy = query(e[i].y);
if (qx != qy) { // 合并两个不在同一连通块的点
cnt++; ans += e[i].z; fa[qx] = qy; // 将边加入最小生成树并统计答案
}
}
if (cnt < n - 1) printf("orz\n");
else printf("%d\n", ans);
return 0;
}
在稠密图中,原版的 Prim 算法时间复杂度较优,但在稀疏图中,堆优化的 Prim 以及 Kruskal 算法表现会更好。在应用时,可以根据实际情况选择合适的算法。
例题:P1396 营救
这是一个典型的“最小化最大值”问题,也称为“瓶颈路问题”(Bottleneck Path Problem)。要在所有从 \(s\) 到 \(t\) 的路径中,找到一条路径,其经过的所有边中权重最大的那条边的权重是所有路径里最小的。
这个问题的解决方案与图的最小生成树密切相关。其核心性质可以表述为:图上任意两点 \(s, t\) 之间的瓶颈路,就是该图的最小生成树上 \(s, t\) 之间的唯一路径。 因此, \(s, t\) 之间的最小瓶颈值等于最小生成树上 \(s, t\) 路径的最大边权。
可以通过分析 Kruskal 算法的执行过程来理解和证明这一点:
-
Kruskal 算法的回顾:Kruskal 算法将所有边按权重从小到大排序,然后依次尝试将边加入图中。如果一条边连接的两个顶点尚不连通,则加入该边;否则,为避免形成环而跳过。
-
寻找瓶颈路:同样将所有边按权重从小到大排序,然后一条一条地加入图中,并用并查集维护连通性。
- 假设加入到第 \(k\) 条边 \(e_k\)(权重为 \(w_k\))时,起点 \(s\) 和终点 \(t\) 首次被连通。
- 这意味着,在只考虑所有权重小于 \(w_k\) 的边时,\(s\) 和 \(t\) 尚不连通。
- 当加入 \(e_k\) 后,\(s\) 和 \(t\) 之间形成了一条路径。这条路径上的所有边的权重都必然小于或等于 \(w_k\)(因为它们都是在 \(e_k\) 或之前被加入的)。因此,这条路径的瓶颈(最大权重)就是 \(w_k\)。这证明了至少可以找到一条瓶颈值为 \(w_k\) 的路径。
-
证明最优性:这个 \(w_k\) 是不是最小的可能瓶颈值呢?
- 假设存在另一条从 \(s\) 到 \(t\) 的路径 \(P'\),其瓶颈值 \(W'\) 小于 \(w_k\)。
- 这意味着路径 \(P'\) 上的所有边的权重都小于 \(w_k\)。
- 那么,在 Kruskal 模拟过程中,路径 \(P'\) 上的所有边都应该在 \(e_k\) 之前被考虑并加入图中。
- 如果是这样,\(s\) 和 \(t\) 应该在加入 \(e_k\) 之前就已经连通了。
- 这与“\(e_k\) 是第一条使 \(s, t\) 连通的边”这一事实相矛盾。
- 因此,不存在瓶颈值小于 \(w_k\) 的路径。
综上所述,在 Kruskal 算法的流程中,当 \(s\) 和 \(t\) 首次连通时,最后加入的那条边的权重,就是 \(s\) 到 \(t\) 的最小瓶颈值。 这就是为什么可以通过模拟 Kruskal 算法来解决这个问题。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 10005; // 最大节点数
const int MAXM = 20005; // 最大边数
// 边结构体
struct Edge {
int u, v, w; // 边的两个端点和权重(拥挤度)
// 重载小于运算符,用于按权重排序
bool operator<(const Edge& other) const {
return w < other.w;
}
};
Edge e[MAXM];
// 并查集(Disjoint Set Union)结构体
struct DSU {
int par[MAXN];
// 初始化:每个节点自成一个集合
void init(int n) {
for (int i = 1; i <= n; i++) par[i] = i;
}
// 查询(带路径压缩)
int query(int x) {
return par[x] == x ? x : par[x] = query(par[x]);
}
// 合并操作在主函数中实现
};
DSU dsu;
int main()
{
int n, m, s, t; // n:区数, m:大道数, s:起点, t:终点
scanf("%d%d%d%d", &n, &m, &s, &t);
dsu.init(n); // 初始化并查集
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
}
// 核心思路:类似Kruskal算法。将所有道路按拥挤度从小到大排序。
// 依次尝试加入道路,直到起点s和终点t连通。
// 当s和t首次连通时,构成该连通路径的所有边中,拥挤度最大的那条就是刚刚加入的边。
// 因为是按拥挤度从小到大加入的,所以这个值是使得s-t连通的所有路径中,最大拥挤度的最小值。
sort(e + 1, e + m + 1);
int ans = 0; // 记录答案,即s-t连通路径上的最大拥挤度
for (int i = 1; i <= m; i++) {
// 在加入本条边之前,先检查s和t是否已经连通。如果已连通,说明上一轮循环中加入的边已经使它们连通。
// 此时的ans就是上一条边的权重,即为答案,可以直接退出。
if (dsu.query(s) == dsu.query(t)) {
break;
}
// 查找边两端点所在集合的根
int qu = dsu.query(e[i].u);
int qv = dsu.query(e[i].v);
// 如果根不同,说明这条边连接了两个不同的连通分量
if (qu != qv) {
dsu.par[qu] = qv; // 合并两个连通分量
// 更新ans为当前已加入的所有边中的最大拥堵度。
// 因为边是排过序的,所以当前边的拥堵度就是最大的。
ans = max(ans, e[i].w);
}
}
printf("%d\n", ans);
return 0;
}
习题:P1194 买礼物
解题思路
这个问题可以转化为最小生成树问题。
可以将 \(B\) 件物品看作图中的 \(B\) 个节点(编号为 \(1\) 到 \(B\))。为了购齐所有物品,必须支付一定的费用将它们全部“连通”起来。
- 物品之间的连接:如果已经拥有物品 \(I\),可以用 \(K_{I,J}\) 的价格购买物品 \(J\)。这可以看作是节点 \(I\) 和节点 \(J\) 之间有一条权重为 \(K_{I,J}\) 的边。
- 购买第一件物品:购买任何一件物品的初始价格都是 \(A\)。可以引入一个虚拟的“超级源点”(编号为 \(0\)),代表开始购买前的状态。从这个超级源点出发,购买任意一件物品 \(I\) 的花费为 \(A\)。这可以看作是超级源点 \(0\) 和每个物品节点 \(I\) 之间都有一条权重为 \(A\) 的边。
通过以上建模,得到了一个包含 \(B+1\) 个节点(\(0\) 到 \(B\))和两类边的无向图:
- 物品 \(I\) 和 \(J\) 之间的边,权重为 \(K_{I,J}\)。
- 超级源点 \(0\) 和每个物品 \(I\) 之间的边,权重为 \(A\)。
目标是“获得”所有 \(B\) 个物品,这在图上等价于让所有物品节点(\(1\) 到 \(B\))都与超级源点 \(0\) 连通(直接或间接)。为了使总花费最小,实际上是在求这个包含 \(B+1\) 个节点的图的最小生成树。最小生成树的总权重就是要求的最小花费。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 505; // 最大物品数量 B+1
const int MAXM = 200005; // 最大边数 B + B*(B-1)/2
// 定义边结构体
struct Edge {
int i, j, k; // 边的两个端点和权重
// 重载小于运算符,用于排序
bool operator<(const Edge& other) const {
return k < other.k;
}
};
Edge e[MAXM]; // 存储所有边的数组
int cnt, fa[MAXN]; // cnt: 边计数器, fa: 并查集的父节点数组
// 并查集的查找操作(带路径压缩)
int find_root(int x) {
return fa[x] == x ? x : fa[x] = find_root(fa[x]);
}
int main()
{
int a, b; // a: 单独购买价格, b: 物品数量
scanf("%d%d", &a, &b);
// 初始化并查集,每个物品自成一个集合
// 节点 0 作为超级源点,代表“商店”或购买第一个物品的动作
fa[0] = 0;
for (int i = 1; i <= b; i++) {
// 添加从超级源点到每个物品的边,权重为单独购买价格 a
// 这代表了购买第一个物品的选择
e[cnt++] = {0, i, a};
fa[i] = i; // 初始化物品 i 的父节点为自身
}
// 读入优惠价格矩阵,构建物品之间的边
for (int i = 1; i <= b; i++) {
for (int j = 1; j <= b; j++) {
int k;
scanf("%d", &k);
// 只需添加 i < j 的边以避免重复
// k != 0 表示存在优惠(价格可能高于A,但仍是备选边)
if (i < j && k != 0) {
e[cnt++] = {i, j, k};
}
}
}
// Kruskal 算法:对所有边按权重从小到大排序
sort(e, e + cnt);
int ans = 0; // 最小总花费
// 遍历排序后的边
for (int i = 0; i < cnt; i++) {
// 查找边两端点所在集合的根节点
int fi = find_root(e[i].i);
int fj = find_root(e[i].j);
// 如果根节点不同,说明两端点不在同一连通分量
// 这条边是安全的,加入后不会形成环
if (fi != fj) {
ans += e[i].k; // 将边权计入总花费
fa[fi] = fj; // 合并两个集合
}
}
printf("%d\n", ans);
return 0;
}
习题:P1550 [USACO08OCT] Watering Hole G
解题思路
这是一个典型的最小生成树问题。题目要求用最小的成本将所有农场连接到一个水源。
可以将这个问题抽象成一个图论模型:
- 将 \(N\) 个农场看作图中的 \(N\) 个节点(编号 \(1\) 到 \(N\))。
- 在农场 \(i\) 和 \(j\) 之间修建水道的花费 \(P_{i,j}\),可以看作是连接节点 \(i\) 和节点 \(j\) 的一条边,其权重为 \(P_{i,j}\)。
- 在农场 \(i\) 挖井的花费 \(W_i\),可以看作是将节点 \(i\) 连接到一个“虚拟的、统一的水源”的费用。
为了统一处理这两种费用,引入一个超级源点(可以编号为 \(N+1\)),这个点代表了总水源。
- 将“在农场 \(i\) 挖井”这一操作,建模为连接超级源点 \((N+1)\) 和农场节点 \(i\) 的一条边,其权重为挖井的费用 \(W_i\)。
通过这样的建模,原问题就转化成了:在一个包含 \(N+1\) 个节点(\(N\) 个农场 + 1 个超级源点)的无向图中,求其最小生成树。这个最小生成树的总权重,就是所有农场都通上水的最小总花费。因为最小生成树保证了用最小的边权和将所有节点连通,这恰好对应了我们的目标。
可以使用 Prim 算法或 Kruskal 算法来求解这个图的最小生成树。由于这是一个稠密图(节点之间几乎都有边),使用基于邻接矩阵的 Prim 算法是一个不错的选择,其时间复杂度为 \(O(V^2)\),其中 \(V\) 是节点数。
参考代码
#include <cstdio>
const int N = 305; // N的最大值为300,加上超级源点,数组大小设为305
const int INF = 1e9; // 代表无穷大
int w[N], p[N][N], dis[N]; // w:挖井费用, p:邻接矩阵存边权, dis:Prim算法中的距离数组
bool vis[N]; // Prim算法中的访问标记数组
int main()
{
int n; scanf("%d", &n);
// 读入在每个农场i挖井的费用w[i]
for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
// 读入连接农场i和j的水道费用p[i][j]
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
scanf("%d", &p[i][j]);
// --- 图的建模 ---
// 引入一个超级源点 n+1,代表“总水源”
// 从超级源点 n+1 连接到任何一个农场 i 的费用,就等于在农场 i 挖井的费用 w[i]
// 这样,问题就转化为了一个包含 n+1 个节点的图的最小生成树问题
for (int i = 1; i <= n; i++) p[i][n + 1] = p[n + 1][i] = w[i];
int ans = 0; // 最小总花费
// --- Prim 算法求最小生成树 ---
// 初始化dis数组,dis[i]表示节点i到当前生成树的最短距离
for (int i = 1; i <= n + 1; i++) dis[i] = INF;
// 从超级源点 n+1 开始
dis[n + 1] = 0;
// Prim主循环,执行 n+1 次
while (true) {
int u = -1;
// 1. 找到当前未访问的、且离生成树最近的节点 u
for (int i = 1; i <= n + 1; i++) {
if (!vis[i] && (u == -1 || dis[i] < dis[u])) {
u = i;
}
}
// 如果所有节点都已访问,则退出
if (u == -1) break;
// 2. 将节点 u 加入生成树
vis[u] = true;
ans += dis[u]; // 累加费用
// 3. 更新其他未访问节点到生成树的距离
// 用新加入的节点 u 的边去松弛其他节点
for (int i = 1; i <= n + 1; i++) {
if (!vis[i] && p[u][i] < dis[i]) {
dis[i] = p[u][i];
}
}
}
printf("%d\n", ans);
return 0;
}
习题:P1195 口袋的天空
解题思路
这个问题可以被抽象为 用最小的代价将图中的 \(N\) 个节点连接成 \(K\) 个连通分量。
这本质上是最小生成树(MST)问题的一个变种。
- 一个标准的最小生成树问题是要求用最小代价将 \(N\) 个节点连接成 1 个连通分量。这需要选择 \(N-1\) 条边。
- 现在,要求形成 \(K\) 个连通分量。可以想象,从一个包含 \(N\) 个节点的完全不连通的图(即 \(N\) 个连通分量)开始。每加入一条边连接两个不同的连通分量,总连通分量数就会减少 1。
- 为了从 \(N\) 个连通分量变成 \(K\) 个连通分量,需要成功连接 \(N-K\) 次。也就是说,需要选择 \(N-K\) 条边。
为了使总代价最小,应该贪心地选择那些代价最小的边来连接。这正是 Kruskal 算法 的思想。Kruskal 算法通过将所有边按权重从小到大排序,然后依次选取不会形成环的边,这恰好能保证每次都是用当前可选的最小代价来合并两个连通分量。
因此,可以通过模拟 Kruskal 算法的过程,不断加入代价最小的边,直到图中的连通分量数量恰好为 \(K\)。此时累加的边权总和就是最小代价。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXM = 10005; // 最大边数
const int MAXN = 1005; // 最大节点数
// 边结构体
struct Edge {
int x, y, l; // 边的两个端点和长度(代价)
// 重载小于运算符,用于按代价排序
bool operator<(const Edge& other) const {
return l < other.l;
}
};
Edge e[MAXM];
int fa[MAXN]; // 并查集的父节点数组
// 并查集的查询操作(带路径压缩)
int query(int x) {
return fa[x] == x ? x : fa[x] = query(fa[x]);
}
int main()
{
int n, m, k; // N:云朵数, M:关系数, K:目标棉花糖数(连通分量数)
scanf("%d%d%d", &n, &m, &k);
// 初始化并查集,每个云朵最初都是一个独立的连通分量
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &e[i].x, &e[i].y, &e[i].l);
}
// Kruskal算法核心:对所有边按代价从小到大排序
sort(e + 1, e + m + 1);
int cnt = n; // 当前连通分量的数量,初始为 N
int ans = 0; // 最小总代价
// 遍历排序后的边,贪心选择代价最小的边
for (int i = 1; i <= m; i++) {
// 如果连通分量数已经达到 K,说明已构成 K 个棉花糖,无需再加边
// 加再多的边只会减少连通分量数,无法满足恰好为 K 的要求
if (cnt == k) break;
// 查找边两端点所在集合的根
int qx = query(e[i].x);
int qy = query(e[i].y);
// 如果根不同,说明两端点不在同一连通分量,可以加这条边
if (qx != qy) {
cnt--; // 每连接两个分量,总分量数减一
ans += e[i].l; // 累加代价
fa[qx] = qy; // 合并两个连通分量
}
}
// 循环结束后,检查连通分量数是否正好为 K
if (cnt == k) {
printf("%d\n", ans); // 如果是,则找到了最小代价
} else {
// 如果不是(cnt > k),说明即使选了所有有用的边,也无法将连通分量数量减少到 K
printf("No Answer\n");
}
return 0;
}
习题:P2700 逐个击破
解题思路
问题要求用最小的代价去“切断”一些边,使得所有 \(K\) 个特殊点(被占领的城市)互相不连通。
直接思考“切哪条边”比较复杂,可以逆向思考。总代价是固定的(所有公路的破坏代价之和),要求破坏的代价最小,就等价于保留的公路的价值最大。
问题转化为:可以在图中保留一些公路,但必须保证任意两个被占领的城市之间没有路径。为了使保留的公路总价值最大,应该如何选择?
这是一个典型的利用贪心思想和并查集解决的问题,思路类似 Kruskal 算法。
计算出所有公路的破坏代价总和 total_cost。我们的目标是最大化“可以保留的公路”的价值之和 saved_cost。最终答案就是 total_cost - saved_cost。
为了最大化 saved_cost,我们应该优先考虑保留那些破坏代价最高的公路。
将所有 \(N-1\) 条公路按破坏代价从高到低进行排序。初始化一个并查集,每个城市自成一个集合。同时,用一个布尔数组标记某个集合内是否存在被占领的城市。初始时,只有那 \(K\) 个被占领的城市所在的集合标记为 true。
遍历排序后的公路。对于当前公路 \((u, v)\),其破坏代价为 \(c\):
- 查找 \(u\) 和 \(v\) 所在的集合的根节点。
- 判断是否可以保留这条公路。保留的条件是:连接 \(u\) 和 \(v\) 后,不会导致两个原本就包含敌军的连通块被连接起来。 换句话说,两者的标记不能同时为
true。 - 如果可以保留:
- 将这条公路的代价 \(c\) 从
total_cost中减去(或者加到saved_cost中)。 - 合并 \(u\) 和 \(v\) 所在的集合。
- 更新新集合的状态:如果两个集合的标记中任意一个为
true,那么新集合的标记也为true。
- 将这条公路的代价 \(c\) 从
- 如果不可以保留,必须破坏这条路,什么都不做,继续遍历下一条。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 100005;
// occ[i] 标记根节点为 i 的连通块中是否包含被占领的城市
bool occ[MAXN];
// 并查集的父节点数组
int fa[MAXN];
// 并查集查询函数(带路径压缩)
int query(int x) {
return fa[x] == x ? x : fa[x] = query(fa[x]);
}
// 定义公路结构体
struct Road {
int a, b, c;
// 重载小于运算符,用于按代价升序排序
bool operator<(const Road& other) const {
return c < other.c;
}
};
Road r[MAXN];
int main()
{
int n, k;
scanf("%d%d", &n, &k);
// 初始化并查集,每个节点自成一个集合
for (int i = 1; i <= n; i++) fa[i] = i;
// 读入 K 个被占领的城市,并标记
for (int i = 0; i < k; i++) {
int c; scanf("%d", &c); occ[c] = true;
}
LL sum = 0;
// 读入 N-1 条公路,并计算总代价
for (int i = 1; i < n; i++) {
scanf("%d%d%d", &r[i].a, &r[i].b, &r[i].c);
sum += r[i].c;
}
// 按代价对公路进行升序排序
sort(r + 1, r + n);
// 从代价最高的公路开始反向遍历(贪心选择)
for (int i = n - 1; i > 0; i--) {
int a = r[i].a, b = r[i].b;
int qa = query(a), qb = query(b);
// 核心贪心条件:
// 1. a 和 b 不在同一个连通块中 (qa != qb)
// 2. a 和 b 所在的两个连通块不能同时都包含被占领的城市
// 如果满足条件,则可以保留这条路
if (qa != qb && !(occ[qa] && occ[qb])) {
// 保留这条路,意味着节省了破坏它的代价
sum -= r[i].c;
// 合并两个连通块
fa[qa] = qb;
// 更新新连通块的占领状态
if (occ[qa] || occ[qb]) {
occ[qb] = true; // 将占领状态传递给新的根节点
}
}
}
// 最终的 sum 就是必须破坏的公路的最小总代价
printf("%lld\n", sum);
return 0;
}
习题:P4047 [JSOI2010] 部落划分
解题思路
求出这个完全图的最小生成树。因为最小生成树上每一条边删去后两部分之间的最短距离就是这条边的边权本身,所以一种最优的部落划分方案就是删去最小生成树中边权前 \(k-1\) 大的边。也就是说,答案为最小生成树中边权第 \(k-1\) 大的那条边的边权。本题为稠密图,可以用 Prim 算法求出最小生成树后按边权排序即可得到答案,时间复杂度为 \(O(n^2+m)\)。
参考代码
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1005;
const double INF = 1e9;
double dis[N], a[N][N], mst[N];
int x[N], y[N];
bool vis[N];
double calc(double dx, double dy) {
return sqrt(dx * dx + dy * dy);
}
int main()
{
int n, k; scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%d%d", &x[i], &y[i]);
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++) {
a[i][j] = calc(x[i] - x[j], y[i] - y[j]);
a[j][i] = a[i][j];
}
for (int i = 0; i <= n; i++) dis[i] = INF;
int cnt = 0; dis[1] = 0;
while (true) {
int u = 0;
for (int i = 1; i <= n; i++)
if (!vis[i] && dis[i] < dis[u]) u = i;
if (u == 0) break;
vis[u] = true; cnt++; mst[cnt] = dis[u];
for (int i = 1; i <= n; i++) {
if (a[u][i] < dis[i]) dis[i] = a[u][i];
}
}
sort(mst + 1, mst + cnt + 1);
printf("%.2f\n", mst[n - k + 2]);
return 0;
}
习题:P8074 [COCI 2009/2010 #7] SVEMIR
解题思路
题目要求用最小总价将 \(N\) 个星球连通,这是一个典型的最小生成树 问题。星球是图的顶点,每两个星球之间都可能建一条隧道(边),边的权重就是题目定义的建造成本。
一个直接的想法是:构建一个完全图,包含所有 \(\dfrac{N(N-1)}{2}\) 条边,然后用 Kruskal 或 Prim 算法求解。但是 \(N\) 的范围是 \(10^5\), \(N^2\) 级别的边数(约 \(5 \times 10^9\))在时间和空间上都是完全无法接受的。因此,本题的关键在于优化建图,即找到一个边数远小于 \(O(N^2)\) 的子图,并保证这个子图的最小生成树与原完全图的最小生成树相同。
思考一下 Kruskal 算法的本质:它会按边权从小到大的顺序处理所有边。能否证明,对于任意一个点,只需要考虑离它“最近”的几个点,而无需考虑所有点?
答案是可以的。这里的“最近”和题目定义的边权有关。
考虑任意两个星球 \(u\) 和 \(v\)。它们之间的边权是 \(w = \min\{|x_u-x_v|, |y_u-y_v|, |z_u-z_v|\}\)。
一个关键的假设:对于任意一个点 \(u\),在最终的最小生成树中,与它相连的边 \((u, v)\),点 \(v\) 一定是与 \(u\) 在某个坐标轴上距离最近的点之一。
证明:假设在最小生成树中有一条边 \((u, v)\),其权重为 \(w = |x_u - x_v|\) (即 x 轴的差值最小)。现在,将所有星球按照 x 坐标排序。在排序后的序列中,假设 \(u\) 和 \(v\) 之间还存在其他星球 \(p_1, p_2, \dots, p_m\)。根据排序的性质,对于 \(u\) 和它在 x 轴上的邻居 \(p_1\),它们之间的边权 \(\text{cost}(u, p_1) = \min\{|x_u-x_{p_1}|, \dots\} \le |x_u-x_{p1}| \lt |x_u-x_v| = w\)。同理,路径 \(u \to p_1 \to \dots \to p_m \to v\) 上所有相邻点对之间的边权都小于等于 \(w\)。
在 Kruskal 算法的视角下,如果将边 \((u, v)\) 从最小生成树中移除,图会分裂成两个连通块。而路径 \(u \to p_1 \to \dots \to v\) 必然存在一条边,可以重新连接这两个连通块,且这条边的权值不大于 \(w\)。这意味着,可以用这条权值更小(或相等)的边来替换 \((u, v)\),得到一个总权值不增的生成树。由于原始的是最小生成树,所以替换后的也必然是最小生成树。
这个结论说明,不需要考虑所有点对,只需要考虑在 x、y、z 三个坐标轴上分别排序后,每个点的相邻点,由这些点对构成的边集合,已经包含了构成最小生成树的所有必要边。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 300005;
// 结构体 S 复用,既可以表示星球坐标,也可以表示边
// 作为星球时: x,y,z 是坐标, id 是原始编号
// 作为边时: x,y 是端点编号, z 是边权, id 是边的唯一标识
struct S {
int x, y, z, id;
};
S p[N], edges[N * 3]; // 候选边最多有 3*(N-1) 条
int cnt, fa[N];
// 按 x, y, z 坐标排序的比较函数
bool cmp_x(const S& p1, const S& p2) {
return p1.x < p2.x;
}
bool cmp_y(const S& p1, const S& p2) {
return p1.y < p2.y;
}
bool cmp_z(const S& p1, const S& p2) {
return p1.z < p2.z;
}
// 计算两个星球之间的隧道成本
int calc(int i, int j) {
return min(abs(p[i].x - p[j].x), min(abs(p[i].y - p[j].y), abs(p[i].z - p[j].z)));
}
// 优化建图的关键步骤:
// 为当前排好序的星球数组中所有相邻的星球建立一条候选边
void build(int n) {
for (int i = 2; i <= n; i++) {
cnt++;
edges[cnt] = {p[i - 1].id, p[i].id, calc(i - 1, i), cnt};
}
}
// 并查集查询函数(带路径压缩)
int query(int x) {
return fa[x] == x ? x : fa[x] = query(fa[x]);
}
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d%d%d", &p[i].x, &p[i].y, &p[i].z);
p[i].id = i; // 保存原始编号
}
// --- 优化建图 ---
// 1. 按 x 坐标排序,并建立相邻星球间的边
sort(p + 1, p + n + 1, cmp_x);
build(n);
// 2. 按 y 坐标排序,并建立相邻星球间的边
sort(p + 1, p + n + 1, cmp_y);
build(n);
// 3. 按 z 坐标排序,并建立相邻星球间的边
sort(p + 1, p + n + 1, cmp_z);
build(n);
// --- Kruskal 算法 ---
// 按边权(存储在 z 成员中)对所有候选边进行排序
sort(edges + 1, edges + cnt + 1, cmp_z);
LL ans = 0;
// 初始化并查集
for (int i = 1; i <= n; i++) fa[i] = i;
// 遍历排好序的候选边
for (int i = 1; i <= cnt; i++) {
int qx = query(edges[i].x), qy = query(edges[i].y);
// 如果边的两个端点不在同一个连通分量中
if (qx != qy) {
// 则选择这条边,合并连通分量,并累加成本
fa[qx] = qy;
ans += edges[i].z;
}
}
printf("%lld\n", ans);
return 0;
}
习题:P1265 公路修建
解题思路
初看题目,可能会被其复杂的多轮修建和审批规则所迷惑。但仔细分析问题的核心目标:用一定的规则连接所有城市,并计算总长度。这个过程,尤其是“每个城市选择一个与它最近的城市”这一贪心策略,强烈地暗示了这是一个最小生成树问题。
经过分析,可以忽略题目中复杂的规则描述,将其简化为:在一个由 \(n\) 个城市构成的完全图中,边的权重是两点间的欧几里得距离,求该图的最小生成树的总权值。
对于求解最小生成树,通常有两种经典算法:Kruskal 和 Prim。
- Kruskal 算法:需要先计算出所有边的权重,然后对边进行排序。在本题中,图是完全图,有 \(O(N^2)\) 条边。对这么多边进行排序的复杂度是 \(O(N^2 \log N)\),对于 \(N=5000\) 来说会超时。
- Prim 算法:适用于稠密图。Prim 算法从一个起始点开始,逐步扩大生成树的规模。其基本实现的复杂度是 \(O(N^2)\),对于 \(N=5000\)(\(2.5 \times 10^7\) 次操作)是可以在时限内接受的。
因此,本题采用 Prim 算法更合适。
参考代码
#include <cstdio>
#include <cmath>
const int N = 5005;
const double INF = 1e9; // 使用一个大数表示无穷大
int x[N], y[N]; // 存储每个城市的坐标
// dis[i] 存储节点 i 到当前已选入MST的节点集合的最短距离
double dis[N];
// vis[i] 标记节点 i 是否已经被选入MST
bool vis[N];
// 计算两点间的欧几里得距离
double euclid_distance(double dx, double dy) {
return sqrt(dx * dx + dy * dy);
}
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &x[i], &y[i]);
dis[i] = INF; // 初始化所有点的距离为无穷大
}
double ans = 0; // 记录MST的总权值
dis[1] = 0; // 从节点1开始执行Prim算法,节点1到自身的距离为0
// Prim算法主循环,执行 n 次
while (true) {
int u = -1;
// 步骤1: 在所有未访问的节点中,找到一个离MST最近的节点 u
for (int i = 1; i <= n; i++) {
if (!vis[i] && (u == -1 || dis[i] < dis[u])) {
u = i;
}
}
// 如果找不到这样的节点,说明所有节点都已加入MST,算法结束
if (u == -1) break;
// 步骤2: 将找到的节点 u 加入MST
vis[u] = true; // 标记 u 为已访问
ans += dis[u]; // 将连接 u 的最短边的权值加入总答案
// 步骤3: 用新加入的节点 u 去更新其他未访问节点到MST的距离
for (int i = 1; i <= n; i++) {
if (vis[i]) continue; // 只更新未访问的节点
double dist = euclid_distance(x[u] - x[i], y[u] - y[i]);
// 如果从 u 出发到 i 的距离比之前记录的距离更短,则更新
if (dist < dis[i]) {
dis[i] = dist;
}
}
}
printf("%.2f\n", ans);
return 0;
}
习题:P5952 [POI 2018] 水箱
解题思路
这是一个计数问题,直接枚举每个格子的水位并判断合法性显然不可行,需要分析合法状态的结构。
水位的性质与连通性密切相关,可以将每个方格看作一个图的顶点,方格间的墙看作连接顶点的边,墙的高度就是边的权重。
当水位从 0 开始慢慢上升时,每次漫过一些高度为 \(w\) 的墙,就会有一些独立的连通块合并成一个更大的连通块。这个过程与使用 Kruskal 算法构建最小生成树的过程完全一致:按边权从小到大将边加入图中,不断合并连通块。
按墙高从小到大处理所有墙(边),在处理过程中,用并查集来维护当前的连通块。
对于并查集中的每个连通块(由其根节点 \(i\) 代表),定义:
- \(\text{maxh}_i\):表示该连通块之所以成为现在的样子,是由于合并了一些更小的连通块,而最后一次合并所通过的墙(也就是当前连通块的“瓶颈”墙高)的高度。
- \(\text{ans}_i\):表示该连通块内,所有可能的合法水位方案数,但前提是水位不能超过 \(\text{maxh}_i\)。
最初,每个方格都是一个独立的连通块。对于单个方格,它的“瓶颈”高度可以看作是 0(因为没有任何内部的墙)。如果水位不能超过 0,那么唯一的方案就是水位为 0。所以,初始化 \(\text{ans}_i=1\),\(\text{maxh}_i=0\) 对于所有方格。
将所有墙按高度 \(w\) 从小到大排序。遍历排序后的墙,假设当前墙连接了两个方格,它们分别属于连通块 \(u\) 和 \(v\)(通过并查集找到的集合根节点)。如果 \(u\) 和 \(v\) 已经是同一个连通块,跳过此墙。如果不同,则意味着当水位上升到 \(w\) 时,这两个连通块将要合并成一个更大的新连通块,需要计算新连通块的 \(\text{ans}\)。
考虑旧的连通块 \(u\),在水位不超过 \(w\) 的情况下,有多少种方案?
- 当水位 \(\le \text{maxh}_u\) 时,方案数为 \(\text{ans}_u\)。
- 当水位在 \((\text{maxh}_u,w]\) 之间时,对于每个这样的水位,整个连通块 \(u\) 内部都必须是这个统一的水位,这样的水位有 \(w-\text{maxh}_u\) 种选择。
- 所以,在水位 \(\le w\) 的前提下,填充连通块 \(u\) 的总方案数是 \(\text{ans}_u+w-\text{maxh}_u\)。
同理,填充连通块 \(v\) 的总方案数是 \(\text{ans}_v+w-\text{maxh}_v\)。
由于在水位低于 \(w\) 时,\(u\) 和 \(v\) 是相互独立的,根据乘法原理,合并后的新连通块在水位 \(\le w\) 时的总方案数就是两者的乘积。
当处理完所有墙后,整个水箱会合并成一个最终的连通块,设其根为 \(\text{root}\)。此时 \(\text{ans}_{\text{root}}\) 代表了在水位 \(\le \text{maxh}_{\text{root}}\) 时的所有合法方案数。剩下的情况是水位高于 \(\text{maxh}_{\text{root}}\),对于任何一个 \(L \in (\text{maxh}_{\text{root}}, H]\),整个水箱的水位都将是统一的 \(L\),因为所有内部的墙都已经被淹没了,这样的方案有 \(H - \text{maxh}_{\text{root}}\) 种。所以,最终的总方案数是 \(\text{ans}_{\text{root}} + H - \text{maxh}_{\text{root}}\)。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e6 + 5;
const int MOD = 1e9 + 7;
// 定义边的结构体,代表墙
struct Edge {
int u, v, w; // u, v 是墙两侧的方格编号,w 是墙高
bool operator<(const Edge& other) const {
return w < other.w;
}
};
Edge a[MAXN * 2]; // 边数组,大小约为 2*n*m
int fa[MAXN]; // 并查集的父节点数组
int maxh[MAXN]; // maxh[i] 表示根为i的连通块的瓶颈墙高
int ans[MAXN]; // ans[i] 表示根为i的连通块在水位<=maxh[i]时的方案数
// 并查集查询函数(带路径压缩)
int query(int x) {
return fa[x] == x ? x : fa[x] = query(fa[x]);
}
int main()
{
int n, m, h;
scanf("%d%d%d", &n, &m, &h);
int len = 0;
// 读入所有水平方向的墙,并构建边
for (int i = 1; i <= n; i++)
for (int j = 1; j < m; j++) {
// 将二维坐标 (i, j) 映射为一维编号
a[len].u = m * (i - 1) + j;
a[len].v = m * (i - 1) + j + 1;
scanf("%d", &a[len].w);
len++;
}
// 读入所有垂直方向的墙,并构建边
for (int i = 1; i < n; i++)
for (int j = 1; j <= m; j++) {
a[len].u = m * (i - 1) + j;
a[len].v = m * i + j;
scanf("%d", &a[len].w);
len++;
}
// 按墙高(边权)从小到大排序
sort(a, a + len);
for (int i = 1; i <= n * m; i++) {
fa[i] = i; // 每个方格自成一个连通块
ans[i] = 1; // 水位<=0时,只有水位为0一种方案
maxh[i] = 0; // 单个方格的瓶颈高度视为0
}
int root = 1; // 记录最终的根节点,任意一个即可
for (int i = 0; i < len; i++) {
int fu = query(a[i].u), fv = query(a[i].v);
if (fu != fv) { // 如果墙连接了两个不同的连通块
// 合并,让 fu 成为新根
fa[fv] = fu;
root = fu;
// new_ans = (ans_u + w - maxh_u) * (ans_v + w - maxh_v)
// 注意处理取模和 long long 防止溢出
ans[fu] = (1LL * (ans[fu] + (LL)a[i].w - maxh[fu]) % MOD * (ans[fv] + (LL)a[i].w - maxh[fv]) % MOD) % MOD;
// 更新新连通块的瓶颈高度
maxh[fu] = a[i].w;
}
}
// 计算最终答案
// ans[root] 是水位 <= maxh[root] 的方案数
// h - maxh[root] 是水位 > maxh[root] 的方案数
printf("%d\n", (ans[root] + h - maxh[root]) % MOD);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号