Reinforce-Rej

机构：Salesforce AI Research
链接：https://arxiv.org/abs/2504.11343
alpharxiv🌟：1200+

insight

在这项工作中，我们从一种类似于增强的算法视角重新审视GRPO 并分析其核心组件。令人惊
讶的是，我们发现一个简单的拒绝采样基准RAFT，它仅在正向奖励样本上进行训练，其性能与GRPO 和PPO 相比具有竞争力。我们的消融研究揭示了GRPO 的主要优势来源于丢弃完全错误响应的提示，而不是来自其奖励规范化。

method

RAFT

• RAFT（就是拒绝采样+SFT）
  • 数据采集。对于一个批量的提示 \(\{x_{1}, \cdots, x_{M}\}\)，我们从参考模型（例如，当前模型）中为每个提示抽取 \(n\) 个响应，以获得每个 \(x_{i}\) 的候选响应 \(\{a_{i,1}, \cdots, a_{i,n}\}\)。
  • 数据排名（拒绝采样）。对于每个提示 \(x_{i}\)，我们使用二元奖励函数 \(r(x, a)\) 计算每个响应 \(\{r_{i,1}, \cdots, r_{i,n}\}\) 的奖励值，并仅保留具有最高奖励的响应（通常为 \(r=1\)）。由此得到的正例集合被聚合为一个数据集 \(D\)。
  • 模型微调。然后针对所选数据集的最大化对数似然，对当前策略 \(\pi\) 进行微调：

\[\mathcal{L}^{\mathrm{RAFT}}(\theta) = \sum_{(x, a) \in \mathcal{D}} \log \pi_{\theta}(a | x). \]

Reinforce（直接使用奖励作为优势）

为了简单起见，我们以将动作作为一个整体（也就是说，将LLM生成的一段话看作一个动作，在这个场景下，奖励（一步的收益）=回报（多步的总收益），最大化期望回报=最大化期望奖励）来说明这个想法，并稍后扩展到自回归模型。策略梯度算法旨在解决以下学习目标：

\[J(\theta) = J(\pi_\theta) = \mathbb{E}_{x \sim d_0} \left[ \mathbb{E}_{a \sim \pi_\theta(\cdot|x)} r(x, a) \right], \]

其中x表示状态，也就是用户输入；\(d_0\)表示状态分布，也就是整个题库；\(\mathbb{E}_{x \sim d_0}\)表示模型在整个数据集上的均值。a表示动作，也就是模型生成的响应，\(\pi_\theta(\cdot|x)\)表示模型给定提示x，生成a的概率，\(\mathbb{E}_{a \sim \pi_\theta(\cdot|x)}\)表示给定提示x，模型生成的所有输出的概率平均。\(r(x, a)\)是奖励。 \(\theta\) 是神经网络的参数。

我们可以使用策略上升来更新策略网络：

\[ \theta' \leftarrow \theta + \beta \cdot \nabla_\theta J(\theta), \]

其中 \(\nabla_\theta J(\theta)\) 在文献中被称为 策略梯度。策略梯度由下式给出：

\[ \frac{\partial J(\theta)}{\partial \theta} = \mathbb{E}_{x \sim d_0} \left[ \mathbb{E}_{a \sim \pi_\theta(\cdot|x)} \left[ \frac{\partial \log \pi_\theta(a|x)}{\partial \theta} \cdot r(x, a) \right] \right]. \]

在 实 践 中 , 类 似 于 RAFT 的 流 水 线 , 我 们 通 常 使 用 \(\pi _{\theta _{\mathrm{old}}}\)将轨迹收集到经验池\(\mathcal{D}\)中，并使用这些样本来计算随机性策略梯度以更新\(\pi_{\theta_\mathrm{old}}\)。然而，对于严格的同策略训练，我们必须在单步梯度上升后收集新的数据。
为了加速训练，我们通常以小批量方式执行多步操作，并采用重要性采样技术来校正分布。具体来说，我们可以重写目标函数为：

\[ J(\theta)=J(\pi_\theta)=\mathbb{E}_{x\sim d_0}\left[\mathbb{E}_{a\sim\pi_{\theta_{\mathrm{old}}}(\cdot|x)}\left[\frac{\pi_\theta(a|x)}{\pi_{\theta_{\mathrm{old}}}(a|x)}r(x,a)\right]\right]. \]

然后，使用由\(\pi_{\theta_{old}}\)收集的批量轨迹\(\{x,a,r\}\),我们可以使用上述重要性采样技巧更新多个步骤。然而， 如果\(\pi_\mathrm{\theta}\)和\(\pi_\mathrm{\theta_\mathrm{old}}\)的分布相差太远，重要性采样可能导致高方差，进而导致训练不稳定。

为了稳定训练，我们还可以利用 PPO 中的裁剪技术。最后，损失函数为：

\[\mathcal{L}^\text{Reinforce}{(\theta)}=\frac1{|\mathcal{D}|}\sum_{x,a\in\mathcal{D}}\Big[\min\Big(\frac{\pi_\theta(a|x)}{\pi_{\theta_\text{old}}(a|x)}r(x,a),\mathrm{clip}(\frac{\pi_\theta(a|x)}{\pi_{\theta_\text{old}}(a|x)},1-\epsilon,1+\epsilon)\cdot r(x,a)\Big)\Big]. \]

由于 LLM 是自回归的，我们通常将每个词元视为一个动作。因此，我们可以将损失扩展到词元级的对应项：

\[\mathcal{L}^\text{Reinforce}(\theta)=\frac1{|\mathcal{D}|}\sum_{x,a\in\mathcal{D}}\frac1{|a|}\sum_{t=1}^{|a|}\Big[\min\Big(s_t(\theta),\mathrm{clip}(s_t(\theta),1-\epsilon,1+\epsilon)\cdot r(x,a)\Big)\Big], \]

其中\(s_t(\theta)=\frac{\pi_\theta(a_t|x,a_{1:t-1})}{\pi_{\theta_\mathrm{old}}(a_t|x,a_{1:t-1})}\)和\(a_t\)是\(t\)的第\(a\)个 Token。

GRPO（使用组间相对优势）

采用了一个与上面相似的损失函数，但用优势函数\(A_t(x,a)\)替换了\(r(x,a)\), 该优势函数是针对响应\(a\)的第\(t\)个词元计算的。具体来说，对于每个提示\(x\), GRPO 将采样\(n>1\)个响应，并为第 i 个响应的第\(t\)个词元计算以下优势：

\[A_t(x,a_i)=\frac{r_i-\text{mean}(r_1,\cdots r_n)}{\text{std}(r_1,\cdots,r_n)}. \]

mean\(( r_1, \cdots r_n)\)在 RL 文献中常被称为基准，用于降低随机梯度的方差。

迭代DPO

DPO 算法依赖于成对型比较数据集\(\{(x,a^+,a^-)\}\) ,其中\(a^+\succ a^-\)是对提示符\(x\)的两个响应。然后，DPO 优化以下对比损失：

\[\mathcal{L}^\mathrm{DPO}(\theta)=-\log\sigma\Big(\beta\log\frac{\pi_\theta(a^+|x)}{\pi_\mathrm{ref}(a^+|x)}-\beta\log\frac{\pi_\theta(a^-|x)}{\pi_\mathrm{ref}(a^-|x)}\Big), \]

其中\(\beta>0\)和\(\pi_\mathrm{ref}\)通常被设置为初始检查点。原始 DPO 算法在离线和异策略数据上进行训练。在后续研究中， 表明我们可以迭代地使用中间检查点生成新的响应，标记偏好信号，并在自生成的同策略数据上进行训练，以显著提高模型性能。

RAFT++（RAFT+重要性采样+剪裁）

我们注意到 RAFT 也可以被视为一种混合算法，在每次迭代中对经验池执行多步操作时可以是异策略。作为一个自然的扩展，我们将重要性采样和裁剪技术应用于原始 RAFT，得到了类似

\[\mathcal{L}^{\mathrm{RAFT}++}(\theta)=\frac{1}{|\mathcal{D}|} \sum_{x, a \in \mathcal{D}} \frac{1}{|a|} \sum_{t=1}^{|a|}\left[\min \left(s_{t}(\theta), \operatorname{clip}\left(s_{t}(\theta), 1-\epsilon, 1+\epsilon\right) \cdot \mathcal{I}\left(r(x, a)=\mathrm{argmax}_{i} r(x, a_{i})\right)\right)\right], \]

其中指示符确保我们只对具有最高奖励（正例）的响应进行训练。

QA

1. 为什么使用\(\min(w(x)\cdot r,clip()\cdot r)\)而不是直接使用\(clip()\cdot r\)？
   基本思想：当且仅当“重要性比率”与“优势信号”同向越界时，才会触发裁剪限制。。这是在鼓励回调，限制冒进

• 同向越界：策略已经朝某个方向（增大概率或减小概率）变化很大，而优势信号确认这个方向是对的。
  • 例子：好动作，比率 \(r > 1 + \epsilon\)（概率已经提得很高），\(A > 0\)（确实好）。
  • 风险：继续优化会导致策略过于“贪婪”、失去随机性，并且新旧策略差异过大，下次估计失效。
  • 对策：触发裁剪，梯度为零，停下来！让其他动作有机会被优化。
• 反向越界：策略变化方向与优势信号指示的方向相反。
  • 例子：好动作，比率 \(r < 1 - \epsilon\)（概率被压得很低），\(A > 0\)（其实好）。
  • 风险：策略正在“错杀忠良”。
  • 对策：不触发裁剪，允许回调，赶紧纠正！

优势 A 的符号	比率 r 相对于区间	是否触发 Clip（限制更新）	逻辑解释
A > 0 (好动作)	r > 1 + ε (过高)	是	防止过度优化一个好动作
A > 0 (好动作)	r < 1 - ε (过低)	否	允许回调，增加好动作的概率
A < 0 (坏动作)	r > 1 + ε (过高)	否	允许回调，减少坏动作的概率
A < 0 (坏动作)	r < 1 - ε (过低)	是	防止过度惩罚一个坏动作

exp

基本观察

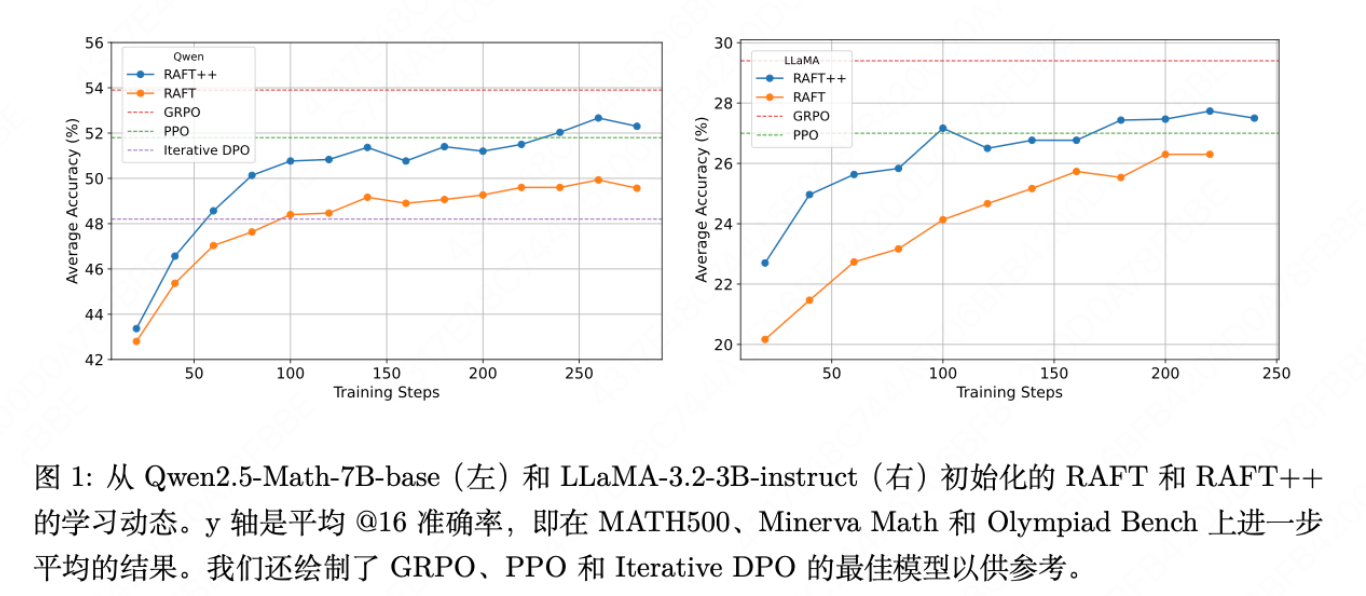
1. 最简单的RAFT方法，其性能与复杂的PPO和迭代DPO相当，甚至更具竞争力。其改进版RAFT++的表现更是接近当前最先进的GRPO。
   

2. 在RAFT基础上引入重要性采样和裁剪（即RAFT++）是有效的，它带来了更快的收敛速度和更高的最终性能，如表1所示。但作者也发现，裁剪是关键，如果只加重要性采样而不加裁剪，效果反而会变差（见图2），这纠正了此前认为裁剪不重要的观点。

两个问题

为什么RAFT++初期收敛快，但GRPO最终超越了GRPO

1. 性能转折点：RAFT++在训练早期收敛极快，但在约100轮迭代后增速放缓，最终被GRPO超越（见图1、2）。这引出了一个核心问题：为什么会有这个转折点？GRPO超越RAFT++的真正原因是什么？
   ![[Pasted image 20251216131354.png]]
2. 作者比较了RAFT++和GRPO训练过程中的策略熵（衡量策略的随机性或探索性）和KL散度（衡量策略相对于初始模型的变化程度）。
3. 发现：如图3所示，RAFT++的策略熵下降极快，意味着模型迅速变得“固执”，只倾向于生成它认为正确的答案，减少了探索新解法的可能性。这解释了其中后期性能增长乏力的问题。相比之下，GRPO通过利用包含负例（错误答案）的样本，更好地保持了策略的探索性。
   

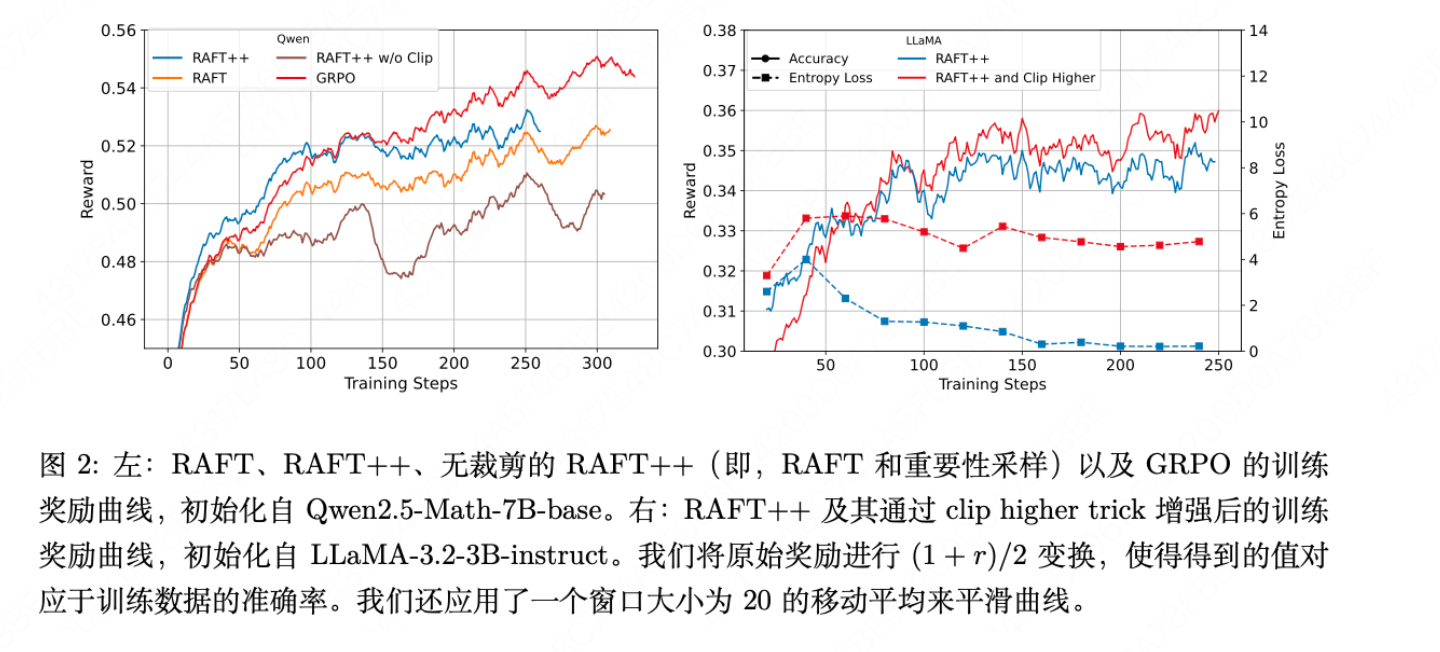
GRPO真正有效的组件是什么

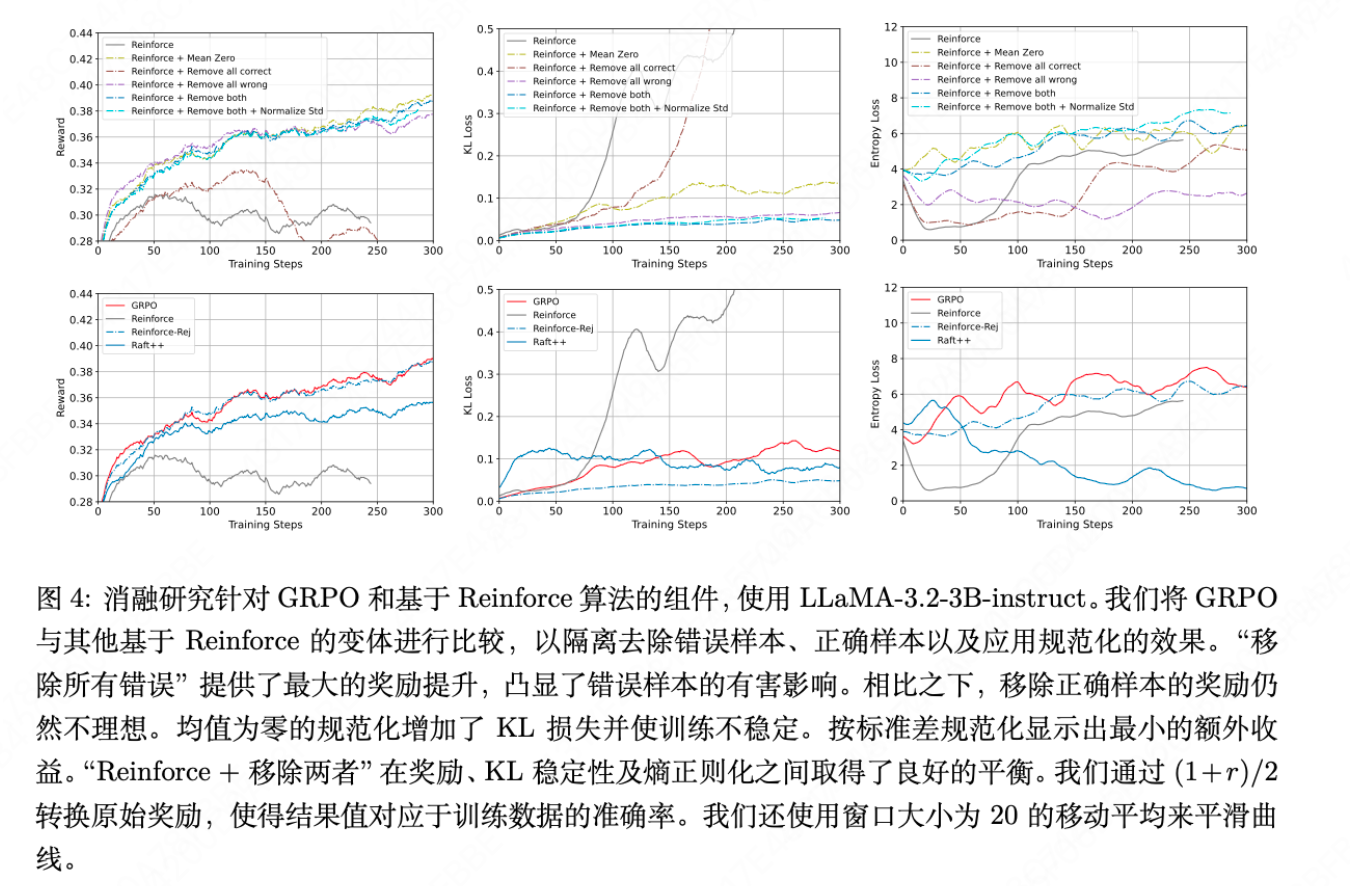
GRPO被认为有效的两个组件是：A. 奖励标准化（减去均值除以标准差）和 B. 使用了所有样本（包括正例和负例）。作者通过设计多个Reinforce算法的变体进行隔离测试：

• Reinforce（基准）
• Reinforce + 移除全部错误样本
• Reinforce + 移除全部正确样本
• Reinforce-Rej：移除全部错误和全部正确的样本（当方差为0时，优势为0）

# GRPO: 归一化
scores[i] = (scores[i] - id2mean[index[i]]) / (id2std[index[i]] + epsilon)

# REINFORCE-REJ: 不归一化
if id2std[index[i]] > 0:
    scores[i] = scores[i]  # 保持原值
else:
    scores[i] = 0  # 如果组内无方差，advantage=0

• Reinforce-Rej + 标准差标准化
  

• 核心发现：性能提升的最大贡献来自于“移除全部错误样本”。也就是说，GRPO的成功主要不是因为它巧妙地对所有样本进行了加权，而是因为它隐式地过滤掉了那些所有生成结果都错误的、极具干扰性的提示。