Python作业2 蒙特卡洛方法手搓图形

定义：蒙特卡罗方法又称统计模拟法、随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法，是使用随机数（或伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名。
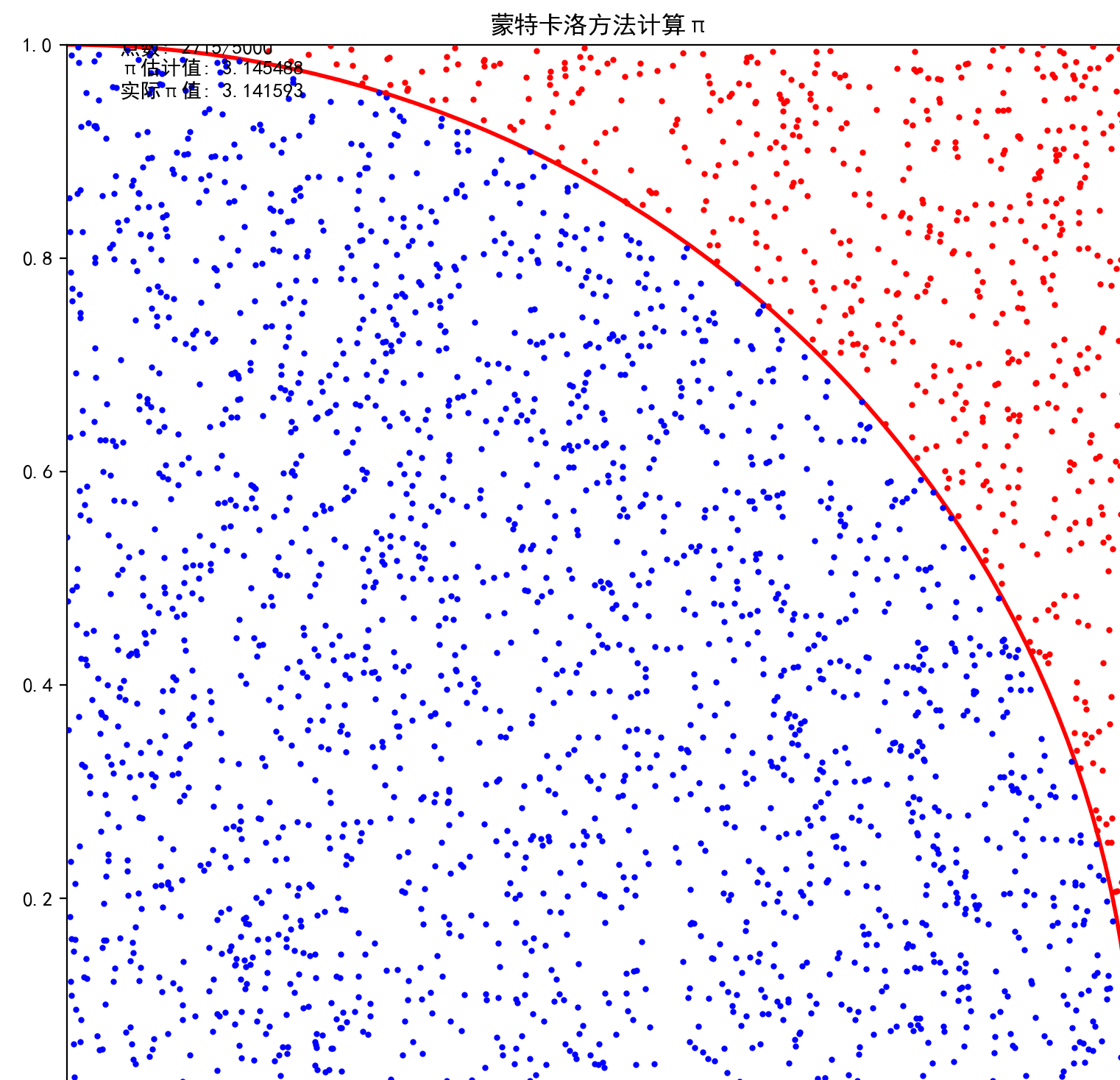
蒙特卡洛方法计算 π 的可视化模拟：

点击查看代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

def monte_carlo_pi_visual(num_points=1000, animation=True):
    """
    使用蒙特卡洛方法计算π并可视化
    
    参数:
    num_points: 生成的随机点数
    animation: 是否使用动画展示过程
    """
    # 创建图形和轴
    fig, ax = plt.subplots(figsize=(8, 8))
    ax.set_xlim(0, 1)
    ax.set_ylim(0, 1)
    ax.set_aspect('equal')
    ax.set_title('蒙特卡洛方法计算π')
    
    # 绘制四分之一圆
    circle = plt.Circle((0, 0), 1, fill=False, color='red', linewidth=2)
    ax.add_patch(circle)
    
    # 初始化散点图
    points_inside, = ax.plot([], [], 'bo', markersize=2)
    points_outside, = ax.plot([], [], 'ro', markersize=2)
    
    # 添加文本显示当前的π估计值
    pi_text = ax.text(0.05, 0.95, '', transform=ax.transAxes)
    
    # 初始化内部和外部点的坐标列表
    inside_x, inside_y = [], []
    outside_x, outside_y = [], []
    
    def init():
        points_inside.set_data([], [])
        points_outside.set_data([], [])
        pi_text.set_text('')
        return points_inside, points_outside, pi_text
    
    def update(frame):
        nonlocal inside_x, inside_y, outside_x, outside_y
        
        # 生成随机点
        x, y = np.random.rand(2)
        
        # 判断点是否在圆内
        if x**2 + y**2 <= 1:
            inside_x.append(x)
            inside_y.append(y)
        else:
            outside_x.append(x)
            outside_y.append(y)
        
        # 更新散点图
        points_inside.set_data(inside_x, inside_y)
        points_outside.set_data(outside_x, outside_y)
        
        # 计算π的估计值
        total_points = len(inside_x) + len(outside_x)
        pi_estimate = 4 * len(inside_x) / total_points if total_points > 0 else 0
        
        # 更新文本
        pi_text.set_text(f'点数: {total_points}/{num_points}\nπ估计值: {pi_estimate:.6f}\n实际π值: {np.pi:.6f}')
        
        return points_inside, points_outside, pi_text
    
    if animation:
        # 创建动画
        ani = FuncAnimation(fig, update, frames=range(num_points),
                            init_func=init, blit=True, interval=1, repeat=False)
    else:
        # 非动画模式：一次性生成所有点
        for _ in range(num_points):
            update(None)
    
    plt.tight_layout()
    plt.show()
    
    # 返回最终的π估计值
    total_points = len(inside_x) + len(outside_x)
    return 4 * len(inside_x) / total_points if total_points > 0 else 0

if __name__ == "__main__":
    # 调整这个参数可以改变模拟的点数
    # 点数越多，π的估计越准确，但计算时间也越长
    estimated_pi = monte_carlo_pi_visual(num_points=5000, animation=True)
    print(f"最终π估计值: {estimated_pi:.8f}")    

运行截图：