Python实验3 函数与代码复用

目的：理解函数封装与递归思想
实验任务：

1. 基础 ：编写函数cal_factorial(n)计算阶乘（循环实现）。
   源码：

点击查看代码

def cal_factorial(n):
    result = 1
    for i in range(1, n + 1):
        result *= i
    return result



try:
    number = int(input("请输入一个整数来计算它的阶乘: "))
    if number < 0:
        print("负数没有阶乘，请输入一个非负整数。")
    else:
        factorial = cal_factorial(number)
        print(f"{number} 的阶乘是: {factorial}")
except ValueError:
    print("输入无效，请输入一个有效的整数。")

运行截图：

2. 进阶 ：用递归实现斐波那契数列（考虑添加缓存优化）。
   源码：

点击查看代码

# 用于存储已经计算过的斐波那契数
fib_cache = {}


def fibonacci(n):
    """
    此函数使用递归和缓存优化来计算斐波那契数列的第 n 项。
    :param n: 要计算的斐波那契数列的位置
    :return: 斐波那契数列的第 n 项的值
    """
    # 检查是否已经计算过该值
    if n in fib_cache:
        return fib_cache[n]
    # 基本情况
    if n == 0 or n == 1:
        result = n
    else:
        # 递归计算
        result = fibonacci(n - 1) + fibonacci(n - 2)
    # 将计算结果存入缓存
    fib_cache[n] = result
    return result


if __name__ == "__main__":
    try:
        # 从控制台获取用户输入
        n = int(input("请输入要计算斐波那契数列的位置（非负整数）: "))
        if n < 0:
            print("输入无效，请输入一个非负整数。")
        else:
            # 调用函数计算斐波那契数
            result = fibonacci(n)
            print(f"斐波那契数列的第 {n} 项是: {result}")
    except ValueError:
        print("输入无效，请输入一个有效的非负整数。")

运行截图：

3. 拓展 ：科赫曲线正向、反向绘制，加入绘制速度、绘制颜色等额外功能
   源码：

点击查看代码

import turtle


def koch(t, order, size, speed, color):
    t.speed(speed)
    t.pencolor(color)
    if order == 0:
        t.forward(size)
    else:
        koch(t, order - 1, size / 3, speed, color)
        t.left(60)
        koch(t, order - 1, size / 3, speed, color)
        t.right(120)
        koch(t, order - 1, size / 3, speed, color)
        t.left(60)
        koch(t, order - 1, size / 3, speed, color)


def draw_koch_snowflake(order, size, speed, color, is_reverse=False):
    t = turtle.Turtle()
    screen = turtle.Screen()
    if is_reverse:
        t.right(180)
    for _ in range(3):
        koch(t, order, size, speed, color)
        t.right(120)
    screen.exitonclick()


# 正向绘制雪花
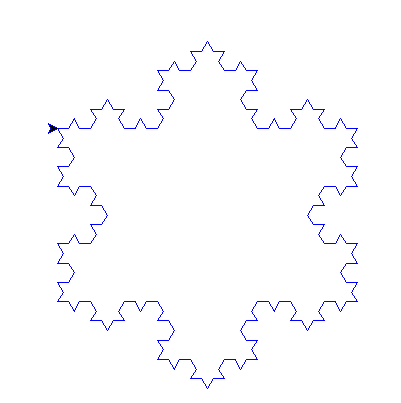
draw_koch_snowflake(order=3, size=300, speed=3, color="blue", is_reverse=False)

# 反向绘制雪花
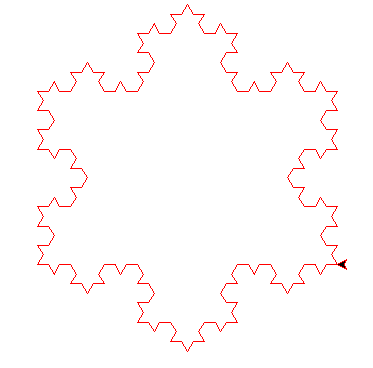
draw_koch_snowflake(order=3, size=300, speed=3, color="red", is_reverse=True)

正向运行截图：

反向绘制运行截图：