2021 暑假水题选做
P1850 [NOIP2016 提高组] 换教室
先用 Floyd 预处理出任意两点之间的最短路 \(\operatorname{dis}(u,v)\),然后 dp。
设 \(f_{i,j,0/1}\) 表示考虑前 \(i\) 门课,有 \(j\) 门课换教室,第 \(i\) 节课是否换教室的答案。
转移就按照第 \(i\) 次换不换与第 \(i-1\) 次换不换分类:
最终的答案就是 \(\min_{i=0}^m\{f_{n,i,0},f_{n,i,1}\}\)。
P3830 [SHOI2012] 随机树
\(q=1\):设 \(f_i\) 表示 \(i\) 个叶子时的答案。我们考虑到当由 \(i-1\) 个叶子变成 \(i\) 个叶子时,会少掉一个期望深度为 \(f_{i-1}\) 的叶子并多出两个期望深度为 \(f_{i-1}+1\) 的叶子,于是:
\(q=2\):设 \(f_{i,j}\) 表示 \(i\) 个叶子时树深度 \(\ge j\) 的概率(注意是概率不是答案),那么
引理:当从 \(i-1\) 个叶子扩展到 \(i\) 个叶子时,不论根的左子树有多少个叶子,根的右子树有多少个叶子,他们的方案数(也即概率)是一样的。
证:设左子树有 \(k\) 个叶子,那么右子树有 \(i-k\) 个叶子。
对于第 \(l\) 次操作,有 \(l\) 个叶子可供扩展,那么左子树的形态有 \((k-1)!\) 种(进行了 \(k-1\) 次操作),右子树的有 \((i-k-1)!\) 种,一共就有 \((k-1)!(i-k-1)!\) 种。
接下来考虑生成它的方案数,可以把它看成是一个由 \(k-1\) 个“扩展左子树”操作和 \(i-k-1\) 个“扩展右子树”操作组成的操作序列,于是方案数为 \(\binom{k-1+i-k-1}{k-1}=\frac{(i-2)!}{(k-1)!(i-k-1)!}\)。
总的方案数为 \((k-1)!(i-k-1)!\cdot \frac{(i-2)!}{(k-1)!(i-k-1)!}=(i-2)!\)。这个式子与 \(k\) 无关!证毕。
有了这个结论,转移方程就出来了:
P2473 [SCOI2008] 奖励关
按照套路设 \(f_{i,S}\) 表示前 \(i\) 个宝物,拿了的宝物集合为 \(S\) 时的答案。然后你发现顺着推不太行。
于是考虑倒着推,设 \(f_{i,S}\) 表示在第 \(1\) 轮到第 \(i-1\) 轮内宝物是否取过的状态为 \(S\),第 \(i\) 轮到第 \(k\) 轮的答案。枚举下一轮出来了哪个宝物,则:
最终答案就是 \(f_{1,\varnothing}\)。
CF906D Power Tower
用扩欧递归求解即可,递归次数不会超过 \(\log p\)。
CF1439C Greedy Shopping
对于操作 1,要操作的地方是完整的一段。
对于操作 2,要操作的地方是完整的若干段,段数不超过 \(\log\) 级别。
这样就可以转化成一个线段树可以解决的问题了。
具体的做法是线段树二分。操作 1 比较简单,重点讲操作 2。
维护区间和和区间 \(\min\)。首先如果 \(r\lt x\) 或者区间 \(\min\) 比 \(y\) 大,则无解。然后如果这个区间能取就取。最后就往左右子树递归。
P3545 HUR-Warehouse Store
贪心。如果能满足就满足,否则,我们要尽可能地去满足他和他后面的人。此时我们应该放弃前面的人中买了最多东西的人(当然前提是那个人之前没被放弃),用放弃他所省下来的钱去满足当前的人和他后面的人。
要用一个堆维护 前面的人中买了最多东西的人。
CF484A Bits
贪心策略:尽量往低位填 \(1\)。
P1792 [国家集训队] 种树
反悔贪心。
维护一个美观度的大根堆。每次取出堆顶然后把答案加上它,然后删掉它旁边的两棵树。
但是同时取两边的树可能比取这棵树要优。所以我们要反悔:弄一个双向循环链表,取堆顶元素 \(a_i\) 时把 \(a_i\) 变成 \(a_{pre_i}+a_{nxt_i}-a_i\)(这就是反悔)再插回去,同时在链表中删去 \(pre_i\) 和 \(nxt_i\)。
P4310 绝世好题
暴力:设 \(f_i\) 为只考虑 \(a_1\sim a_i\) 且 \(a_i\) 必须选时的答案,则
正解:每次转移的时候按位考虑,设 \(f_{i,j}\) 表示只考虑 \(a_1\sim a_i\),二进制第 \(j\) 位的答案(注意这里不一定要取 \(a_i\))。那么
然后这个 dp 状态的第一维可以压掉。
P1484 种树
P1792 双倍经验。
P3620 [APIO/CTSC 2007] 数据备份
P1792 三倍经验。
SP1553 BACKUP - Backup Files
P1792 四倍经验。
P4158 [SCOI2009] 粉刷匠
这个题是一个背包:设 \(f_{i,j}\) 表示考虑前 \(i\) 个木板,粉刷了 \(j\) 次的答案。则:
后面的玩意要用另外一个 dp 做:设 \(g_{i,j,k}\) 表示第 \(i\) 个模板,前 \(j\) 个格子,粉刷了 \(k\) 次最多刷对的格子个数,则:
P1772 [ZJOI2006] 物流运输
设 \(f_i\) 表示前 \(i\) 天的答案,那么我们考虑枚举 \(j\),使得在 \(j+1\) 天换航线,\(j+1\sim i\) 航线不变,那么:
其中 \(d_{i,j}\) 表示在 \(i\sim j\) 天时 \(1\to m\) 的最短路。
P2939 [USACO09FEB] Revamping Trails G
设 \(f_{i,u}\) 表示当前在 \(u\) 结点,用了 \(i\) 次高速的答案,那么:
P3874 [TJOI2010] 砍树
树上背包模板。设 \(f_{u,j}\) 表示以 \(u\) 为根的子树选 \(j\) 个点的答案。则:
P1941 [NOIP2014 提高组] 飞扬的小鸟
设 \(f_{i,j}\) 表示横坐标为 \(i\),高度为 \(j\) 时最少的点击次数。
转移时分三类考虑:从 \(i-1\) 往上走而来,从 \(i\) 继续往上而来,从 \(i-1\) 往下掉而来。
注意 \(j=m\) 时要特殊考虑。
P4374 [USACO18OPEN] Disruption P
直接做不好做,考虑每条新边对答案的贡献。
显然一条边 \((u,v)\) 只能对 \(u,v\) 间的路径做贡献,然后这题就做完了。
注意这里的树剖要边权转点权。
P3976 [TJOI2015] 旅游
CF985F Isomorphic Strings
挺妙的一道题。
我们考虑一个字母在这个区间的出现状况,用 \(\texttt{01}\) 表示,然后对这个串 hash。
对 \(26\) 个字母都这么做一遍,如果对于一个字母有一个和它对应的 hash 值(就是说 \(26\) 个字母和 \(26\) 个 hash 值构成一一映射),那么这个是可行的。
CF961F k-substrings
考虑当一个字符串的头尾都去掉后,它的 border 会发生什么:
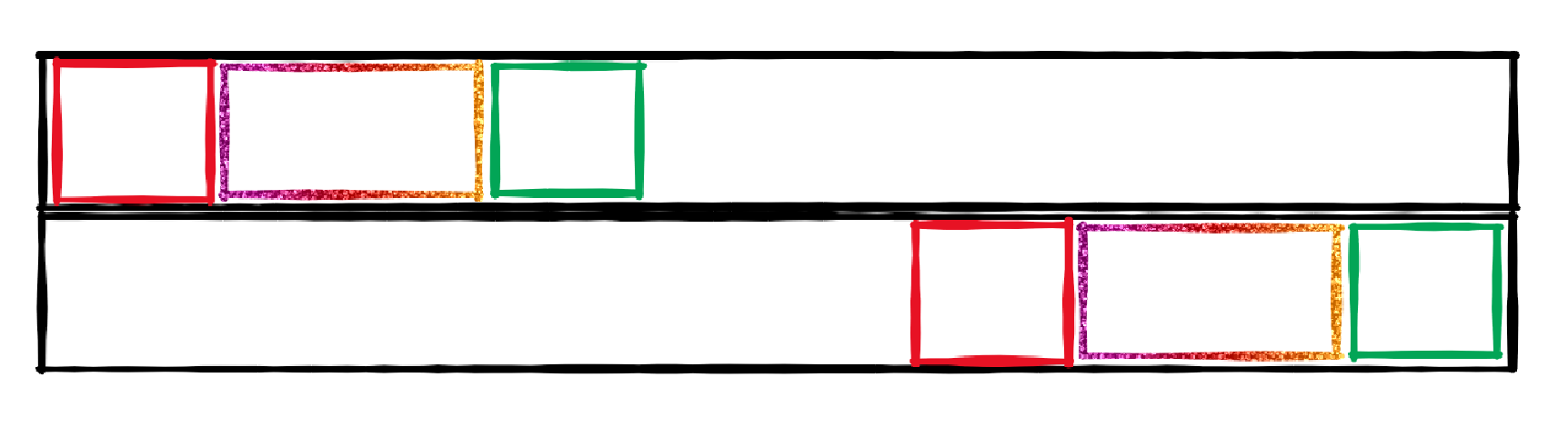
我们发现中间彩色部分依然是一个 border,而且这个新的 border 可能不止彩色部分。
用一个指针维护下 border 的两个端点就行。
CF1144E Median String
把两个字符串看成两个 \(26\) 进制数 \(a,b\),那么答案就是 \(\frac{a+b}2\)。
P2577 [ZJOI2004] 午餐
先按照吃饭时间排序,这样吃饭慢的人先打饭可以节约时间。
然后设 \(f_{i,j}\) 表示前 \(i\) 个人在第 \(1\) 个窗口打饭用了 \(j\) 分钟的答案,那么在第二个窗口就用了 \(sum_i-j\) 分钟打饭。
[NOIP2000 提高组] 乘积最大
设 \(f_{i,j}\) 表示前 \(i\) 位分割 \(j\) 次的答案,则:
于是这个题要用高精,Python 3 水过去。
CF1110D Jongmah
CF282E Sausage Maximization
首先那个区间不能重叠的条件是可以忽略的,因为 \(x\oplus x=0\)。然后就是一个 01trie 了。
CF1525D Armchairs
设 \(f_{i,j}\) 表示前 \(i\) 个人坐前 \(j\) 把椅子的答案,则:
P6394 樱花,还有你
背包 dp + 前缀和优化。
CF1077F1 & CF1077F2 Pictures with Kittens
设 \(f_{i,j}\) 表示考虑 \(a_1\sim a_i\) 选了 \(j\) 个,\(a_i\) 必须选的答案。则:
可以单调队列优化。
有一个细节:枚举 \(j\) 的时候要倒着枚举。
CF459E Pashmak and Graph
先排序,这样就没有后效性了。
设 \(f_i\) 表示考虑前 \(i\) 条边的答案,\(mx_u\) 表示当前考虑到的所有边 \(\langle v,u\rangle\) 中,\(f\) 的最大值。设第 \(i\) 条边为 \(\langle u,v\rangle\),则:
然后因为边权必须是严格递增的,所以每次处理时要把所有边权相同的边一起处理。
P4720 【模板】扩展卢卡斯定理/exLucas
P2183 [国家集训队]礼物
根据小奥知识,答案是 \(\binom{n}{w_1}\binom{n-w_1}{w_2}\cdots\)。
exLucas 计算即可。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号