P3976 [TJOI2015] 旅游 题解

Solution

这个题应该比较好想。如果这是一个序列上的问题，我们就可以用线段树维护一个区间右减左的答案，左减右的答案：

struct Node{
	int mx,mn,lr,rl,atag; // 区间最大值，最小值，左减右，右减左，区间加标记
	Node(){mx=lr=rl=-inf,mn=inf,atag=0;}
};

// 合并两个区间
inline Node pushUp(const Node &L,const Node &R){
	Node res;
	res.mx=std::max(L.mx,R.mx);
	res.mn=std::min(L.mn,R.mn);
	res.lr=std::max(std::max(L.lr,R.lr),L.mx-R.mn);
	res.rl=std::max(std::max(L.rl,R.rl),R.mx-L.mn);
	return res;
}

// 下传区间加标记
inline void pushA(Node &x,int atag){
	x.atag+=atag;
	x.mx+=atag;
	x.mn+=atag;
}

然后因为这是一个树上的问题，所以我们要树剖。然而这个题是那种类似 GSS7 的毒瘤题，所以合并的时候要考虑顺序。

来放几张图：

因为 \(dfn_w\le dfn_u\)，所以合并一条链应该是用上面的去合并下面的：

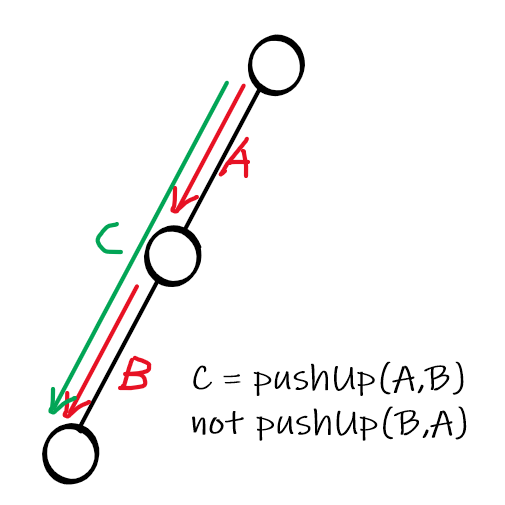
因为 \(dfn_w\le dfn_u,dfn_w\le dfn_v\)，所以合并之后的顺序是这样的：

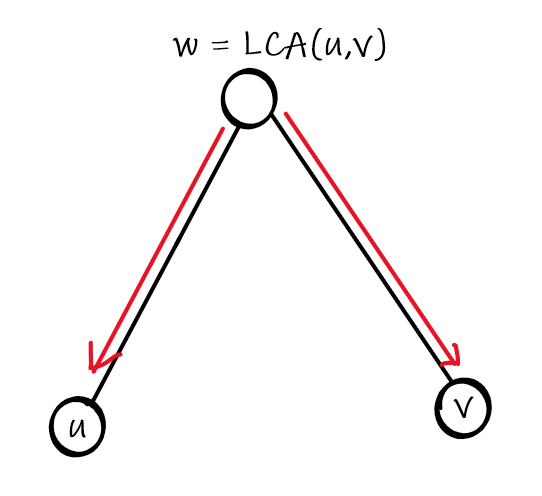
于是我们需要交换一下 \(u\leftrightarrow w\) 这条链上的 lr 和 rl，之后就变成了这样：

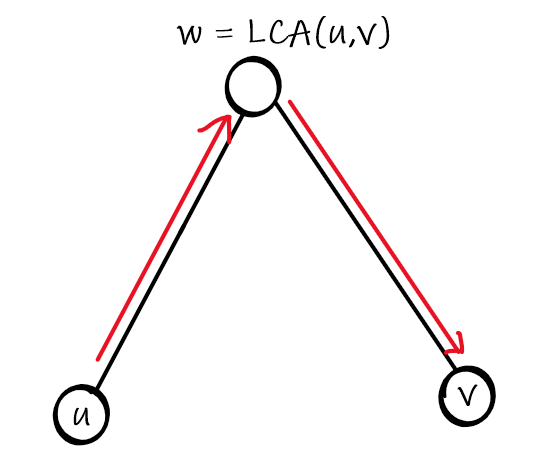
最后把两条链合并即可。

Code

#include<cstdio>
#include<algorithm>

const int N=5e4;
const int inf=0x3f3f3f3f;

struct Edge{int to,nxt;}e[N*2+10];int head[N+10],tote;
inline void addEdge(int u,int v){e[++tote].to=v;e[tote].nxt=head[u];head[u]=tote;}

struct Node{
	int mx,mn,lr,rl,atag;
	Node(){mx=lr=rl=-inf,mn=inf,atag=0;}
};

int n,m,a[N+10];
int fa[N+10],dep[N+10],siz[N+10],son[N+10],dfn[N+10],rk[N+10],top[N+10],cnt;
Node t[N*4+10];

#define ls(x) (x<<1)
#define rs(x) (x<<1|1)

inline Node pushUp(const Node &L,const Node &R){
	Node res;
	res.mx=std::max(L.mx,R.mx);
	res.mn=std::min(L.mn,R.mn);
	res.lr=std::max(std::max(L.lr,R.lr),L.mx-R.mn);
	res.rl=std::max(std::max(L.rl,R.rl),R.mx-L.mn);
	return res;
}

inline void pushA(Node &x,int atag){
	x.atag+=atag;
	x.mx+=atag;
	x.mn+=atag;
}

inline void pushDown(int i){
	if(t[i].atag){
		pushA(t[ls(i)],t[i].atag);
		pushA(t[rs(i)],t[i].atag);
		t[i].atag=0;
	}
}

void build(int i,int l,int r){
	if(l==r){
		t[i].mn=t[i].mx=a[rk[l]];
		t[i].lr=t[i].rl=0;
		return;
	}
	int mid=(l+r)>>1;
	build(ls(i),l,mid);
	build(rs(i),mid+1,r);
	t[i]=pushUp(t[ls(i)],t[rs(i)]);
}

void modify(int i,int l,int r,int ql,int qr,int x){
	if(ql<=l&&r<=qr)return pushA(t[i],x),void();
	int mid=(l+r)>>1;
	pushDown(i);
	if(ql<=mid)modify(ls(i),l,mid,ql,qr,x);
	if(qr>mid) modify(rs(i),mid+1,r,ql,qr,x);
	t[i]=pushUp(t[ls(i)],t[rs(i)]);
}

Node query(int i,int l,int r,int ql,int qr){
	if(ql<=l&&r<=qr)return t[i];
	int mid=(l+r)>>1;
	pushDown(i);
	if(ql>mid) return query(rs(i),mid+1,r,ql,qr);
	if(qr<=mid)return query(ls(i),l,mid,ql,qr);
	return pushUp(query(ls(i),l,mid,ql,qr),query(rs(i),mid+1,r,ql,qr));
}

#undef ls
#undef rs

void DFS1(int u,int _fa){
	fa[u]=_fa;
	dep[u]=dep[_fa]+1;
	siz[u]=1;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==_fa)continue;
		DFS1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>siz[son[u]])son[u]=v;
	}
}

void DFS2(int u,int _fa,int _top){
	dfn[u]=++cnt,rk[cnt]=u;
	top[u]=_top;
	if(son[u])DFS2(son[u],u,_top);
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==_fa||v==son[u])continue;
		DFS2(v,u,v);
	}
}

void modify(int u,int v,int x){
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]])std::swap(u,v);
		modify(1,1,n,dfn[top[u]],dfn[u],x);
		u=fa[top[u]];
	}
	if(dfn[u]>dfn[v])std::swap(u,v);
	modify(1,1,n,dfn[u],dfn[v],x);
}

Node query(int u,int v){
	Node L,R;
	while(top[u]!=top[v]){
		if(dep[top[u]]>dep[top[v]]){
			L=pushUp(query(1,1,n,dfn[top[u]],dfn[u]),L);
			u=fa[top[u]];
		}
		else{
			R=pushUp(query(1,1,n,dfn[top[v]],dfn[v]),R);
			v=fa[top[v]];
		}
	}
	if(dfn[u]<dfn[v])
		R=pushUp(query(1,1,n,dfn[u],dfn[v]),R);
	else
		L=pushUp(query(1,1,n,dfn[v],dfn[u]),L);
	std::swap(L.lr,L.rl);
	return pushUp(L,R);
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",a+i);
	for(int i=1;i<n;i++){
		int u,v;scanf("%d%d",&u,&v);
		addEdge(u,v),addEdge(v,u);
	}
	DFS1(1,0),DFS2(1,0,1),build(1,1,n);
	scanf("%d",&m);
	while(m--){
		int u,v,x;scanf("%d%d%d",&u,&v,&x);
		Node ans=query(u,v);
		printf("%d\n",std::max(0,ans.rl));
		modify(u,v,x);
	}
	return 0;
}