平均应力修正法11

1. 平均应力修正方法

在耐久性设计中，非零平均正应力的存在可以影响材料的疲劳特性，因为拉伸或压缩平均正应力对裂纹的产生和生长具有促进或减弱的作用。试验数据证明，压缩平均正应力对疲劳寿命是有益的，而平均拉应力则对疲劳寿命是有害的。由此还可以观察到，在平均应力大大低于循环屈服应力的情况下，疲劳特性落在弹性应变显著的长寿命区域。
结合局部应变 - 寿命法，提出了许多用于量化平均应力对疲劳特性影响的模型。地面车辆行业通常采用的模型是莫洛模型\({}^{[29]}\)和史密斯 - 沃森 - 腾普模型\({}^{[39]}\)。这些方程都是以经验为基础的，需要与试验数据进行对比，以确定哪个模型最适合于所研究的材料和试验条件。

1.1 莫洛平均应力修正法

莫洛提出了在平均应力存在时的以下关系式。

\[\varepsilon_{\mathrm{a}}=\frac{\sigma_{\mathrm{f}}^{\prime}-\sigma_{\mathrm{m}}}{E}\left(2 N_{\mathrm{f}}\right)^{b}+\varepsilon_{\mathrm{f}}^{\prime}\left(2 N_{\mathrm{f}}\right)^{c}\tag{5.4.1} \]

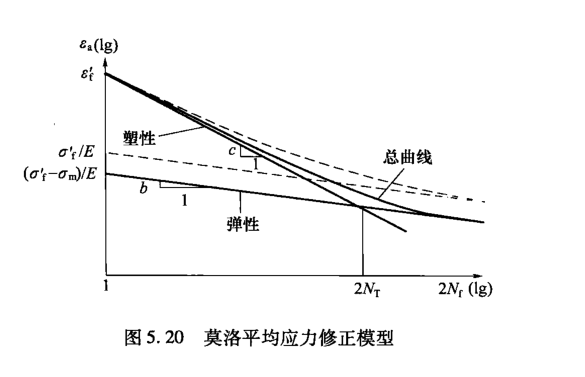
这一方程表明，利用平均应力\((\sigma_{\mathrm{m}})\)修改应变 - 寿命曲线的弹性部分，可以将平均正应力的影响考虑进去。如图5.20所示，该模型表明，拉伸平均应力会降低疲劳强度系数\(\sigma'_{\mathrm{f}}\)，而压缩平均应力会增加疲劳强度系数。该方程广泛应用于钢铁材料，并且当塑性应变幅不起主要作用时在长疲劳寿命区域获得了很大的应用成功。
瓦尔歇（Walcher）、格雷（Gray）和曼森（Manson）1979 年的研究\({}^{[45]}\)表明，对于其它材料（例如 Ti - 6Al - 4V），由于\(\sigma'_{\mathrm{f}}\)值太高而无法对平均应力进行修正，但是中值\(k_{\mathrm{m}}\sigma'_{\mathrm{f}}\)可以通过试验确定。因此，提出了一个广义公式：

\[\varepsilon_{\mathrm{a}}=\frac{k_{\mathrm{m}} \sigma_{\mathrm{f}}^{\prime}-\sigma_{\mathrm{m}}}{E}\left(2 N_{\mathrm{f}}\right)^{b}+\varepsilon_{\mathrm{f}}^{\prime}\left(2 N_{\mathrm{f}}\right)^{c}\tag{5.4.2} \]

这个方程需要额外的试验数据来确定\(k_{\mathrm{m}}\sigma'_{\mathrm{f}}\)。

1.2 史密斯 - 沃森 - 腾普（SWT）模型

史密斯、沃森和腾普于1970年提出了一种模型\({}^{[39]}\)，假设在一个循环中的疲劳损伤量是通过\(\sigma_{\mathrm{max}}\varepsilon_{\mathrm{a}}\)确定的，其中\(\sigma_{\mathrm{max}}\)是最大拉应力，\(\varepsilon_{\mathrm{a}}\)是应变幅。此外，SWT参数只是说明：“对称循环载荷试验的\(\sigma_{\mathrm{a}}\varepsilon_{\mathrm{a}}\)等于平均应力试验中的\(\sigma_{\mathrm{max}}\varepsilon_{\mathrm{a}}\)”。因此，这个概念可以被归纳成如下数学表达式\({}^{[20]}\)：

\[\sigma_{\mathrm{max}} \varepsilon_{\mathrm{a}}=\sigma_{\mathrm{a}, \mathrm{rev}} \varepsilon_{\mathrm{a}, \mathrm{rev}}, \sigma_{\mathrm{max}}>0\tag{5.4.3} \]

式中：

\(\sigma_{\mathrm{a},\mathrm{rev}}\)和\(\varepsilon_{\mathrm{a},\mathrm{rev}}\)分别为对称循环应力幅和应变幅，由此可以产生一个由SWT参数引起的当量疲劳损伤。

\(\varepsilon_{\mathrm{a},\mathrm{rev}}\)的值应该根据应变 - 寿命曲线获得（方程(5.3.20)），而\(\sigma_{\mathrm{a},\mathrm{rev}}\)的值应该根据循环应力 - 应变曲线获得（方程(5.3.15)）。

SWT参数还表明，如果最大拉应力为零或为负值，那么就不存在疲劳损伤。利用牛顿 - 拉斐森（Newton - Raphson）迭代过程，可以得到方程(5.4.3)的解。
对于方程(5.4.3)的一个特例，其中材料特性完全满足一致性条件（即\(n' = b/c\)和\(K' = \sigma'_{\mathrm{f}}/(\varepsilon'_{\mathrm{f}})^{n'}\)），对称循环载荷时的最大拉应力用如下方程给出：

\[\sigma_{\mathrm{max}}=\sigma_{\mathrm{a}}=\sigma_{\mathrm{f}}^{\prime}\left(2 N_{\mathrm{f}}\right)^{b}\tag{5.4.4} \]

将其乘以应变 - 寿命方程，SWT平均应力修正公式可以表示为：

\[\sigma_{\mathrm{max}} \varepsilon_{\mathrm{a}}=\frac{\left(\sigma_{\mathrm{f}}^{\prime}\right)^{2}}{E}\left(2 N_{\mathrm{f}}\right)^{2 b}+\sigma_{\mathrm{f}}^{\prime} \varepsilon_{\mathrm{f}}^{\prime}\left(2 N_{\mathrm{f}}\right)^{b+c}, \sigma_{\mathrm{max}}>0\tag{5.4.5} \]

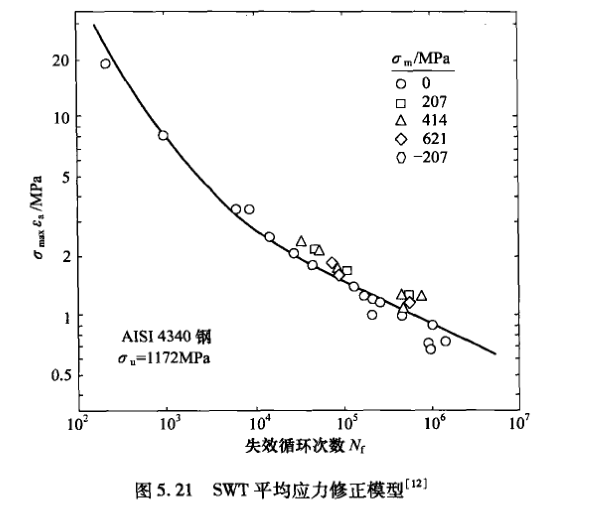
SWT公式已经成功应用于灰铸铁（1982年）\({}^{[14]}\)、淬硬碳钢（1991年）\({}^{[19][44]}\)以及微合金钢（1988年）\({}^{[15]}\)。SWT公式被认为是最有希望推广应用的公式。图5.21将这些具有不同平均应力值的一组疲劳数据合并成一条曲线。由此可见，这些数据点可以用SWT参数表示。

2 数据案例

2.1 例5.5

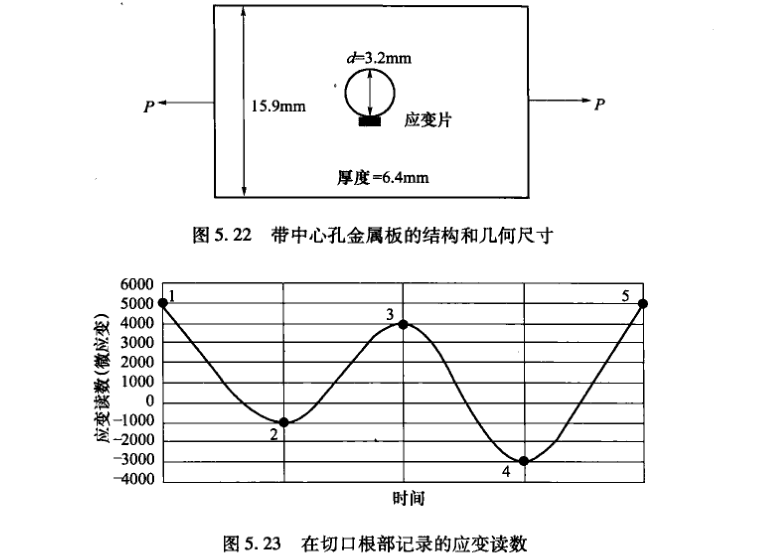
一个有源应变片放置在一个有切口金属板的切口根部，如图5.22所示。

该有切口零件由SAE 1137碳钢制成，其材料特性为：\(E = 209000\mathrm{MPa}\)，\(K' = 1230\mathrm{MPa}\)，\(n' = 0.16\)；\(\sigma'_{\mathrm{f}} = 1006\mathrm{MPa}\)，\(b = -0.0809\)，\(\varepsilon'_{\mathrm{f}} = 1.104\)，\(c = -0.6207\)。

外加载荷引起的应变时间历程记录是重复的，如图5.23所示。

（1）绘制循环应力 - 应变响应（滞后回线）；
（2）应用SWT方程估算有切口金属板的疲劳寿命；
（3）应用莫洛方程估算有切口金属板的疲劳寿命。
解：为确定滞后回线，必须首先确立初始加载状态，然后是第一个加载反复以及所有的后续循环。

首先考虑初始加载。初始加载从零应变开始，逐步增至\(5000\mu\varepsilon\)。

为了定义在加载过程中由应力 - 应变关系得到的曲线，对沿着应变路径上众多的点进行分析是非常重要的。初始加载时，对于0.005的值采用了0.0005的步距。为了确定应变每一个中间步的应力，采用循环应力 - 应变方程进行计算：

\[\varepsilon_{1} = \frac{\sigma_{1}}{E} + \left( \frac{\sigma_{1}}{K'} \right)^{\frac{1}{n'}} \]

例如，在\(\varepsilon_{1} = 0.005\)时，\(\sigma_{1}\)可以通过如下方程计算：

\[0.005 = \frac{\sigma_{1}}{209000} + \left( \frac{\sigma_{1}}{1230} \right)^{\frac{1}{0.16}} \]

解\(\sigma_{1}\)得到：

\[\sigma_{1} = 475.35\mathrm{MPa} \]

表5.9列出了在初始加载阶段每一个\(\sigma\)和\(\varepsilon\)增量的值。

详细代码见附录4.1

​ 表5.9 点1的初始加载：真实应力和应变的数据点

\(\boxed{\varepsilon_1}\)	0.0005	0.0010	0.0015	0.0020	0.0025	0.0030	0.0035	0.0040	0.0045	0.0050
\(\boxed{\sigma_1}\)/MPa	104.45	205.85	288.10	342.98	380.21	407.65	429.24	447.03	462.17	475.35

确定初始加载条件之后，这时可以检查第一次加载反复（\(\varepsilon_{1} = 0.0050 \to \varepsilon_{2} = -0.0010\)）。另外，对曲线进行定义也是非常重要的，这样才可以研究众多点相对于基准点（点1）沿着应变轨迹的变化。为了确定应力和应变的变化，采用马辛模型进行计算：

\[\Delta\varepsilon = \frac{\Delta\sigma}{E} + 2\left( \frac{\Delta\sigma}{2K'} \right)^{\frac{1}{n'}} \]

例如，在应变从0.0050变化到-0.0010（\(\Delta\varepsilon = 0.0060\)）时，可以得到应力的变化\(\Delta\sigma\)为

\[0.0060 = \frac{\Delta\sigma}{209000\mathrm{MPa}} + 2\left( \frac{\Delta\sigma}{2 \times 1230} \right)^{\frac{1}{0.16}} \]

解方程，求出\(\Delta\sigma\)

\[\Delta\sigma = 815.30\mathrm{MPa} \]

由于采用马辛模型计算应力变化，必须将该变化与基准应力进行对比（\(\sigma_{1} = 475.35\mathrm{MPa}\)），以确定点2处的应力：

\[\sigma_{2} = \sigma_{1} - \Delta\sigma = 475.35 - 815.30 = -339.95\mathrm{MPa} \]

表5.10列出了在第一个加载反复时，\(\sigma\)和\(\varepsilon\)各个增量的值。见附录4.3

对于第二个加载反复（\(\varepsilon_{2} = -0.0010 \to \varepsilon_{3} = 0.0040\)），除了点2作为新的基准点外，采用了与第一个载荷反复相同的程序。

例如，在\(\Delta\varepsilon = 0.0050\)时，确定\(\Delta\sigma\)：

\[0.0050 = \frac{\Delta\sigma}{209000} + 2\left( \frac{\Delta\sigma}{2 \times 1230} \right)^{\frac{1}{0.16}} \]

解\(\Delta\sigma\)，得

\[\Delta\sigma = 760.42\mathrm{MPa} \]

此外，由于采用马辛模型计算应力变化，必须将该变化与基准应力（\(\sigma_{2} = -339.95\mathrm{MPa}\)）进行比较，以确定在点3处的应力。

\[\sigma_{3} = \sigma_{2} + \Delta\sigma = -339.95 + 760.42 = 420.47\mathrm{MPa} \]

对于第三个或第四个加载反向，也采用了相同的程序。

当材料的响应返回到先前经历过的变形时，材料就会记忆起过去的路线来达到这样一种状态，并将遵循这一路线再增加额外变形。这就是材料在经受复杂加载历程时观察到的所谓记忆效应。在第三个反向中，在从点3到点2较小的反向之后，返回到先前经历过的最大变形——点2，其余的加载反向将沿着从点1到点4的路径变化。表5.11~表5.13列出了在第二、第三和第四次加载反向时，每个增量的\(\sigma\)和\(\varepsilon\)值。

根据初始载荷和反向载荷计算的这些点，绘制了如图5.24所示的滞后回线。

确定滞后回线之后，需要采用SWT法估计疲劳寿命。忽略初始加载，对应变结果进行雨流循环计数分析。采用SWT方程(5.4.3)，在表5.14中确定损伤计算结果。由此获得以下总损伤和疲劳寿命的预测结果：

\[\sum d_{i} = 1.78 \times 10^{-5} + 8.09 \times 10^{5} = 9.87 \times 10^{-5} \]

\[\text{寿命} = \frac{1}{\sum d_{i}} = \frac{1}{9.87 \times 10^{-5}} = 10100\ \text{块循环} \]

为了与SWT法进行对比，采用莫洛法估计疲劳寿命。采用上述雨流计算分析方法以及莫洛方程（方程(5.4.1)），所得出的总损伤计算结果见表5.15。总损伤和疲劳寿命预测如下：

\[\sum d_{i} = 1.48 \times 10^{-5} + 7.35 \times 10^{-5} = 8.83 \times 10^{-5} \]

\[\text{寿命} = \frac{1}{\sum d_{i}} = \frac{1}{8.83 \times 10^{-5}} = 11300\ \text{块循环} \]

3.计算过程

3.1 方程求解

求解下面的方程

\[0.0060 = \frac{\Delta\sigma}{209000\mathrm{MPa}} + 2\left( \frac{\Delta\sigma}{2 \times 1230} \right)^{\frac{1}{0.16}} \]

求解代码

import numpy as np
from scipy.optimize import fsolve

delta_eps = 0.0060

delta_sigma = round(fsolve(lambda s: delta_eps - (s/209000 + 2*(s/(2*1230))**(1/0.161)), 50)[0], 2)
print(f"Δε = {delta_eps} → Δσ = {delta_sigma} MPa")

输出结果

Δε = 0.006 → Δσ = 815.3 MPa

基于表5.1 第二列 Δε 可以算出第三列，然后基于第四列的基准475.35，依次减去Δσ，得到第四列其他值。

​ 表5.1 表 5.10 第一次加载反向 (点 1 到点 2):真实应力和应变数据点

ε	Δε	Δσ/MPa	σ/MPa
0.005	基准点 1	0	475.35
0.0045	0.0005	104.5	370.85
0.004	0.001	208.91	266.44
0.0035	0.0015	312.37	162.98

完整表格见附录4.3

4.附录

4.1 表5.9代码

import numpy as np
from scipy.optimize import fsolve

# 表格中的应变数据（ε₁）
strains = [0.0005, 0.0010, 0.0015, 0.0020, 0.0025, 
           0.0030, 0.0030, 0.0035, 0.0040, 0.0045, 0.0050]

# 定义方程：对于每个应变ε，求解σ使得 ε = σ/209000 + (σ/1230)^(1/0.161)
def equation(sigma, epsilon):
    return epsilon - (sigma / 209000 + (sigma / 1230)** (1 / 0.161))

# 存储结果的列表
results = []

# 遍历每个应变值，求解对应的应力
for eps in strains:
    # 初始猜测值（根据数据范围调整，确保收敛）
    initial_guess = 100  # 从100MPa开始，根据迭代情况自动调整
    
    # 求解方程（传入应变值作为额外参数）
    sigma_sol, = fsolve(equation, initial_guess, args=(eps,))
    
    # 验证误差
    error = equation(sigma_sol, eps)
    
    # 保存结果
    results.append({
        '应变ε': eps,
        '求解应力σ(MPa)': round(sigma_sol, 2),
        '验证误差': round(error, 10)
    })

# 打印结果表格
print("批量求解结果：")
print("-" * 60)
print(f"{'序号':<5} | {'应变ε':<10} | {'求解应力σ(MPa)':<18} | {'验证误差':<15}")
print("-" * 60)
for i, res in enumerate(results, 1):
    print(f"{i:<5} | {res['应变ε']:<10} | {res['求解应力σ(MPa)']:<18} | {res['验证误差']:<15}")

运算结果

批量求解结果：
------------------------------------------------------------
序号    | 应变ε        | 求解应力σ(MPa)         | 验证误差           
------------------------------------------------------------
1     | 0.0005     | 104.45             | 0.0            
2     | 0.001      | 205.85             | 0.0            
3     | 0.0015     | 288.1              | 0.0            
4     | 0.002      | 342.98             | -0.0           
5     | 0.0025     | 380.21             | 0.0            
6     | 0.003      | 407.65             | 0.0            
7     | 0.003      | 407.65             | 0.0            
8     | 0.0035     | 429.24             | 0.0            
9     | 0.004      | 447.03             | 0.0            
10    | 0.0045     | 462.17             | 0.0            
11    | 0.005      | 475.35             | 0.0

4.2 表 5.10 代码

import numpy as np
from scipy.optimize import fsolve

# 表中的Δε数据（11个数据点）
delta_eps_list = [0.0005, 0.0010, 0.0015, 0.0020, 0.0025,
                  0.0030, 0.0035, 0.0040, 0.0045, 0.0050, 0.0060]

# 基准点1的应力（σ基准 = 475.35 MPa）
sigma_base = 475.35

# 修正后的方程：用Δσ的绝对值计算（避免负数幂运算）
def equation(sigma_abs, delta_eps):
    """
    sigma_abs: Δσ的绝对值（正数，待求）
    delta_eps: 当前应变变化量
    返回方程误差（目标为0）
    """
    term1 = sigma_abs / 209000  # 弹性应变项（绝对值不影响线性关系）
    term2 = 2 * (sigma_abs / (2 * 1230)) ** (1 / 0.161)  # 塑性应变项（用绝对值保证底数为正）
    return delta_eps - (term1 + term2)

# 存储结果
results = []

# 遍历每个Δε，求解Δσ
for delta_eps in delta_eps_list:
    # 初始猜测值（σ_abs为正数，根据应变范围调整为合理值）
    initial_guess = 50  # 从50MPa开始（避免初始值过小/过大导致收敛失败）
    
    # 求解Δσ的绝对值（设置求解器参数，提升收敛性）
    sigma_abs_sol, info, ier, msg = fsolve(
        equation, initial_guess, args=(delta_eps,),
        full_output=True, maxfev=1000  # 增加最大迭代次数
    )
    
    # 反向加载：Δσ = -绝对值（应力减小，为负值）
    delta_sigma = -sigma_abs_sol[0]
    
    # 计算最终应力σ = 基准应力 + Δσ
    sigma = sigma_base + delta_sigma
    
    # 验证误差（代入绝对值验证方程）
    error = equation(sigma_abs_sol[0], delta_eps)
    
    # 保存结果（保留2位小数）
    results.append({
        'Δε': delta_eps,
        '|Δσ|(MPa)': round(sigma_abs_sol[0], 2),
        'Δσ(MPa)': round(delta_sigma, 2),
        'σ(MPa)': round(sigma, 2),
        '验证误差': round(error, 10),
        '收敛状态': '成功' if ier == 1 else '失败'
    })

# 打印结果表格
print("第一次加载反向（点1到点2）计算结果（修正后）：")
print("-" * 90)
print(f"{'序号':<5} | {'Δε':<10} | {'|Δσ|(MPa)':<12} | {'Δσ(MPa)':<12} | {'σ(MPa)':<12} | {'验证误差':<15} | {'收敛状态':<8}")
print("-" * 90)
for i, res in enumerate(results, 1):
    print(
        f"{i:<5} | {res['Δε']:<10} | {res['|Δσ|(MPa)']:<12} | "
        f"{res['Δσ(MPa)']:<12} | {res['σ(MPa)']:<12} | {res['验证误差']:<15} | {res['收敛状态']:<8}"
    )

计算结果

第一次加载反向（点1到点2）计算结果（修正后）：
------------------------------------------------------------------------------------------
序号    | Δε         | |Δσ|(MPa)    | Δσ(MPa)      | σ(MPa)       | 验证误差            | 收敛状态    
------------------------------------------------------------------------------------------
1     | 0.0005     | 104.5        | -104.5       | 370.85       | 0.0             | 成功      
2     | 0.001      | 208.91       | -208.91      | 266.44       | 0.0             | 成功      
3     | 0.0015     | 312.37       | -312.37      | 162.98       | -0.0            | 成功      
4     | 0.002      | 411.7        | -411.7       | 63.65        | 0.0             | 成功      
5     | 0.0025     | 501.15       | -501.15      | -25.8        | 0.0             | 成功      
6     | 0.003      | 576.2        | -576.2       | -100.85      | 0.0             | 成功      
7     | 0.0035     | 636.88       | -636.88      | -161.53      | 0.0             | 成功      
8     | 0.004      | 685.96       | -685.96      | -210.61      | 0.0             | 成功      
9     | 0.0045     | 726.38       | -726.38      | -251.03      | -0.0            | 成功      
10    | 0.005      | 760.42       | -760.42      | -285.07      | -0.0            | 成功      
11    | 0.006      | 815.3        | -815.3       | -339.95      | -0.0            | 成功

4.3 表5.10-5.13

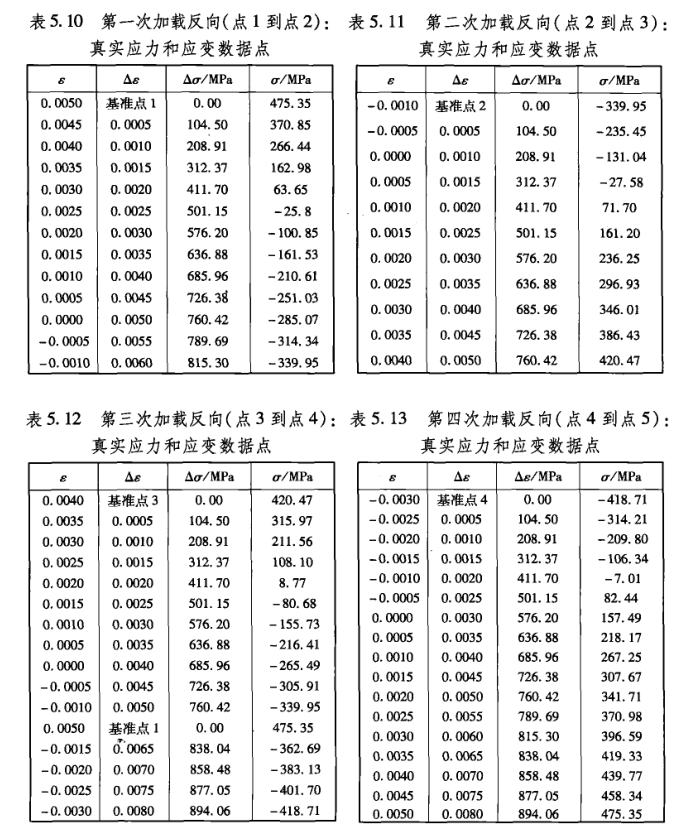
4.4 应力应变汇总

ε	σ/MPa	ε	σ/MPa	ε	σ/MPa	ε	σ/MPa	ε	σ/MPa
0.0005	104.45	0.005	475.35	-0.001	-339.95	0.004	420.47	-0.003	-418.71
0.001	205.85	0.0045	370.85	-0.0005	-235.45	0.0035	315.97	-0.0025	-314.21
0.0015	288.1	0.004	266.44	0	-131.04	0.003	211.56	-0.002	-209.8
0.002	342.98	0.0035	162.98	0.0005	-27.58	0.0025	108.1	-0.0015	-106.34
0.0025	380.21	0.003	63.65	0.001	71.7	0.002	8.77	-0.001	-7.01
0.003	407.65	0.0025	-25.8	0.0015	161.2	0.0015	-80.68	-0.0005	82.44
0.0035	429.24	0.002	-100.85	0.002	236.25	0.001	-155.73	0	157.49
0.004	447.03	0.0015	-161.53	0.0025	296.93	0.0005	-216.41	0.0005	218.17
0.0045	462.17	0.001	-210.61	0.003	346.01	0	-265.49	0.001	267.25
0.005	475.35	0.0005	-251.03	0.0035	386.43	-0.0005	-305.91	0.0015	307.67
		0	-285.07	0.004	420.47	-0.001	-339.95	0.002	341.71
		-0.0005	-314.34			0.005	475.35	0.0025	370.98
		-0.001	-339.95			-0.0015	-362.69	0.003	396.59
						-0.002	-383.13	0.0035	419.33
						-0.0025	-401.7	0.004	439.77
						-0.003	-418.71	0.0045	458.34
								0.005	475.35

4.5 应力应变画图

# 数据1：第一组（左1列）
data1 = [
    (0.0005, 104.45), (0.001, 205.85), (0.0015, 288.1), (0.002, 342.98),
    (0.0025, 380.21), (0.003, 407.65), (0.0035, 429.24), (0.004, 447.03),
    (0.0045, 462.17), (0.005, 475.35)
]

# 数据2：第二组（左2列）
data2 = [
    (0.005, 475.35), (0.0045, 370.85), (0.004, 266.44), (0.0035, 162.98),
    (0.003, 63.65), (0.0025, -25.8), (0.002, -100.85), (0.0015, -161.53),
    (0.001, -210.61), (0.0005, -251.03), (0, -285.07), (-0.0005, -314.34),
    (-0.001, -339.95)
]

# 数据3：第三组（左3列）
data3 = [
    (-0.001, -339.95), (-0.0005, -235.45), (0, -131.04), (0.0005, -27.58),
    (0.001, 71.7), (0.0015, 161.2), (0.002, 236.25), (0.0025, 296.93),
    (0.003, 346.01), (0.0035, 386.43), (0.004, 420.47)
]

# 数据4：第四组-1（左4列前半段）
data4_1 = [
    (0.004, 420.47), (0.0035, 315.97), (0.003, 211.56), (0.0025, 108.1),
    (0.002, 8.77), (0.0015, -80.68), (0.001, -155.73), (0.0005, -216.41),
    (0, -265.49), (-0.0005, -305.91), (-0.001, -339.95)
]
# 数据4：第四组-2（左4列后半段）
data4_2 = [
    (-0.0015, -362.69), (-0.002, -383.13), (-0.0025, -401.7),
    (-0.003, -418.71)
]

# 数据5：第五组（右1列）
data5 = [
    (-0.003, -418.71), (-0.0025, -314.21), (-0.002, -209.8), (-0.0015, -106.34),
    (-0.001, -7.01), (-0.0005, 82.44), (0, 157.49), (0.0005, 218.17),
    (0.001, 267.25), (0.0015, 307.67), (0.002, 341.71), (0.0025, 370.98),
    (0.003, 396.59), (0.0035, 419.33), (0.004, 439.77), (0.0045, 458.34),
    (0.005, 475.35)
]



import matplotlib.pyplot as plt

plt.figure(figsize=(14, 8))

# --------------------------
# 1. 绘制第1条曲线：第一组数据
# --------------------------
eps1, sig1 = zip(*data1)
plt.plot(eps1, sig1, color='blue', linewidth=1.5, label='第1组曲线', alpha=0.8)
plt.scatter(eps1, sig1, color='blue', s=30, alpha=0.9, edgecolors='white', linewidth=0.3)
plt.scatter(eps1[0], sig1[0], color='blue', s=100, marker='o', edgecolors='black', linewidth=1)
plt.scatter(eps1[-1], sig1[-1], color='blue', s=120, marker='*', edgecolors='black', linewidth=1)

# --------------------------
# 2. 绘制第2条曲线：第二组数据
# --------------------------
eps2, sig2 = zip(*data2)
plt.plot(eps2, sig2, color='orange', linewidth=1.5, label='第2组曲线', alpha=0.8)
plt.scatter(eps2, sig2, color='orange', s=30, alpha=0.9, edgecolors='white', linewidth=0.3)
plt.scatter(eps2[0], sig2[0], color='orange', s=100, marker='o', edgecolors='black', linewidth=1)
plt.scatter(eps2[-1], sig2[-1], color='orange', s=120, marker='*', edgecolors='black', linewidth=1)

# --------------------------
# 3. 绘制第3条曲线：第三组数据
# --------------------------
eps3, sig3 = zip(*data3)
plt.plot(eps3, sig3, color='green', linewidth=1.5, label='第3组曲线', alpha=0.8)
plt.scatter(eps3, sig3, color='green', s=30, alpha=0.9, edgecolors='white', linewidth=0.3)
plt.scatter(eps3[0], sig3[0], color='green', s=100, marker='o', edgecolors='black', linewidth=1)
plt.scatter(eps3[-1], sig3[-1], color='green', s=120, marker='*', edgecolors='black', linewidth=1)

# --------------------------
# 4. 绘制第4条曲线：第四组-1
# --------------------------
eps4_1, sig4_1 = zip(*data4_1)
plt.plot(eps4_1, sig4_1, color='darkgreen', linewidth=1.5, label='第4组-1曲线', alpha=0.8, linestyle='--')
plt.scatter(eps4_1, sig4_1, color='darkgreen', s=30, alpha=0.9, edgecolors='white', linewidth=0.3)
plt.scatter(eps4_1[0], sig4_1[0], color='darkgreen', s=100, marker='o', edgecolors='black', linewidth=1)
plt.scatter(eps4_1[-1], sig4_1[-1], color='darkgreen', s=120, marker='*', edgecolors='black', linewidth=1)

# --------------------------
# 5. 绘制第5条曲线：第四组-2
# --------------------------
eps4_2, sig4_2 = zip(*data4_2)
plt.plot(eps4_2, sig4_2, color='limegreen', linewidth=1.5, label='第4组-2曲线', alpha=0.8, linestyle='-.')
plt.scatter(eps4_2, sig4_2, color='limegreen', s=30, alpha=0.9, edgecolors='white', linewidth=0.3)
plt.scatter(eps4_2[0], sig4_2[0], color='limegreen', s=100, marker='o', edgecolors='black', linewidth=1)
plt.scatter(eps4_2[-1], sig4_2[-1], color='limegreen', s=120, marker='*', edgecolors='black', linewidth=1)

# --------------------------
# 6. 绘制第6条曲线：第五组数据
# --------------------------
eps5, sig5 = zip(*data5)
plt.plot(eps5, sig5, color='red', linewidth=1.5, label='第5组曲线', alpha=0.8)
plt.scatter(eps5, sig5, color='red', s=30, alpha=0.9, edgecolors='white', linewidth=0.3)
plt.scatter(eps5[0], sig5[0], color='red', s=100, marker='o', edgecolors='black', linewidth=1)
plt.scatter(eps5[-1], sig5[-1], color='red', s=120, marker='*', edgecolors='black', linewidth=1)

# --------------------------
# 图表配置
# --------------------------
plt.xlabel('真实应变 ε', fontsize=11)
plt.ylabel('真实应力 σ / MPa', fontsize=11)
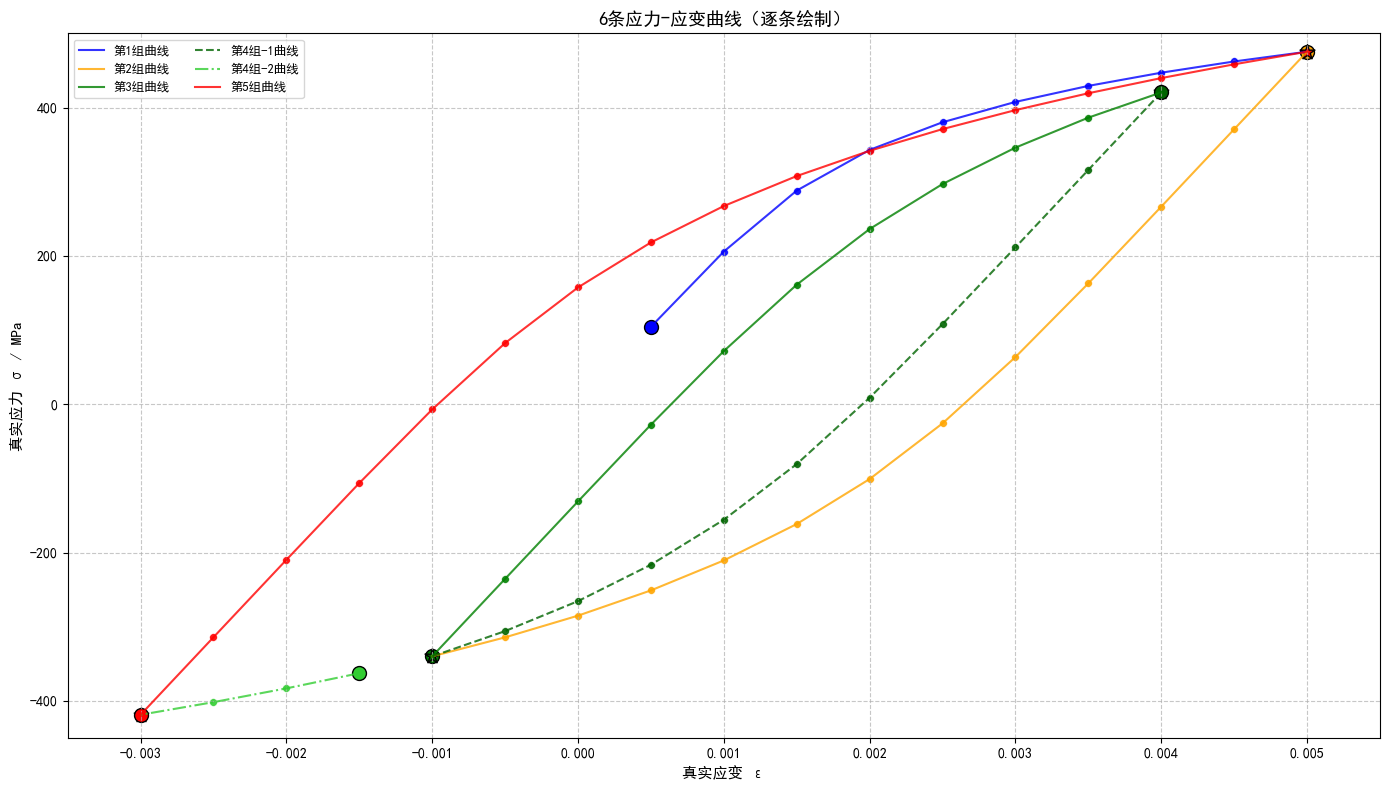
plt.title('6条应力-应变曲线（逐条绘制）', fontsize=13)
plt.grid(linestyle='--', alpha=0.7, linewidth=0.8)
plt.legend(loc='upper left', fontsize=9, ncol=2)
plt.xlim(-0.0035, 0.0055)
plt.ylim(-450, 500)
plt.tight_layout()
plt.show()