疲劳数据分析与设计曲线 25
1 计算方法
1.1 回归分析
在S-N试验中,一旦收集到有限寿命区域的疲劳寿命数据,则推荐采用最小二乘法来生成与数据最佳拟合的一条直线。对于疲劳数据的统计分析,这种生成最佳拟合直线的方法是可行的。因为在应力幅与疲劳交变循环次数的双对数特性图上,8这些疲劳数据可以表示为一条直线。假设在给定应力幅水平下,疲劳寿命遵循对数正态分布,并且记录寿命的方差在整个试验范围内为常数。在统计学中,这种对于所有应力水平都具有恒方差的假设,被定义为同方差性假设。最小二乘法回归模型为
式(4.2.2)中,\(\varepsilon\)是误差的随机变量。回归线是
式(4.2.3)中,\(\hat{A}\)和\(\hat{B}\)的估算值可以通过使预测中观察值\(Y\)离差的平方和最小化来得到,例如,
式(4.2.4)中,试样数用变量\(n_{\text{s}}\)表示。由此可以得到以下方程:
据此,采用最小二乘法对\(\hat{B}\)和\(\hat{A}\)作如下估算:
式中:\(\bar{X}\)和\(\bar{Y}\)分别为\(X\)和\(Y\)的平均值(例如,\(\bar{X} = \sum X_i/n_{\text{s}}\)和\(\bar{Y} = \sum Y_i/n_{\text{s}}\))。
假设在\(X_i\)的变化范围内,\(Y_i\)相对于\(X_i\)而变化的偏差量(即,残余均方差)为常数,可用如下方程描述:
式中:\(s\)为估计值\(Y_i\)相对于\(X_i\)的试样标准差。
在S-N方程(方程(4.1.6))两边取对数(均为以10为底的对数或自然对数),对方程进行重新整理得到如下方程:
这个方程中,采用\(\lg\)。将方程(4.2.10)与最小二乘方程\(Y = \hat{A} + \hat{B}X\)进行比较,由此可以确定\(X = \lg(S_a)\)是自变量;\(Y = \lg(2N_f)\)是因变量。同样,对最小二乘方程中的系数取\(\hat{A} = (-1/b)\lg S'_f\)和\(\hat{B} = 1/b\)的形式。
总之,通过如下表达式,可以建立疲劳强度指数\(b\)与线性回归常数\(\hat{B}\)关系:
疲劳强度系数可以计算如下:
采用以10为底的对数时,
采用自然对数时,
为了进行概率设计和分析,推导出了以下统计疲劳特性\(^{[55][26]}\)。假设S-N曲线的斜率\(b\)和估算值\(Y\)相对于\(X\)变化的离差是常数。基于给定的\(s\)(估算值\(Y_i\)相对于\(X_i\)变化的试样标准差),定义\(S'_f(C_{S'_f})\)的变异系数为标准差与平均值之比,估算如下:
对于以\(e\)为底的对数:
对于以10为底的对数:
1.2 设计曲线
本节介绍结构建设计S-N曲线的实用方法,用于描述给定疲劳强度条件下最低疲劳寿命的特性,使大部分疲劳数据落在最小值或下界值以上。
图4.5示出了典型的设计S-N曲线的示意图。
下界S-N曲线(即所谓的设计S-N曲线)的选择是靠经验的,与材料成本、安全措施和行业标准相关。例如,如果将一个R95C90的值用于零件设计,这个特定值确保:在一个规定应力水平上,具有90%置信水平的存活率为95%(可靠性)。由于样本容量通常受到限制,引入90%置信水平,以确保实际上95%的可靠性值预计落在此下界以上的概率为90%。
传统上,工程协会更愿意采用较低的2-σ或3-σ设计曲线。将对数坐标的中值S-N曲线左移两倍或三倍的试样标准差,推导出该设计曲线。这意味着设计曲线可表示如下:
式中:s为Y在\(X_i\)上的样本标准误差;K为等于2或3的乘数;\(Y_{\text{L}}\)被定义为在已知\(X_i\)(=\(S_{\text{a},i}\))时Y的下界(=\(2N_{\text{f}}\)或\(N_{\text{f}}\))。在凯塞西奥格鲁2003年的著作中\(^{[18]}\),可以找出这种应用实例。然而,这些方法不能将由样本容量和所研究可靠性水平引起的疲劳寿命统计分布考虑在内。
为了克服上述缺点,李博曼(Lieberman)于1958年提出了另一种设计曲线方法学\(^{[24]}\),即单侧下界公差极限方法。根据\(X_i\)上的样本容量\(Y_i\),将中值S-N曲线左移K倍,获得设计S-N曲线。当在固定应力幅下对试样进行试验时,并且变量(例如记录寿命)只遵循正态分布,这种方法是有效的。当进行回归分析时,X和Y均为变量,这种方法因其只考虑了变量Y而出现错误。
为了考虑回归分析中的不确定性:
- ASTM 1998年提出了双测量置信区间法\(^{[2]}\);
- 沈等人1996年提出了近似欧文(Owen)单侧公差极限法\(^{[40]}\)。
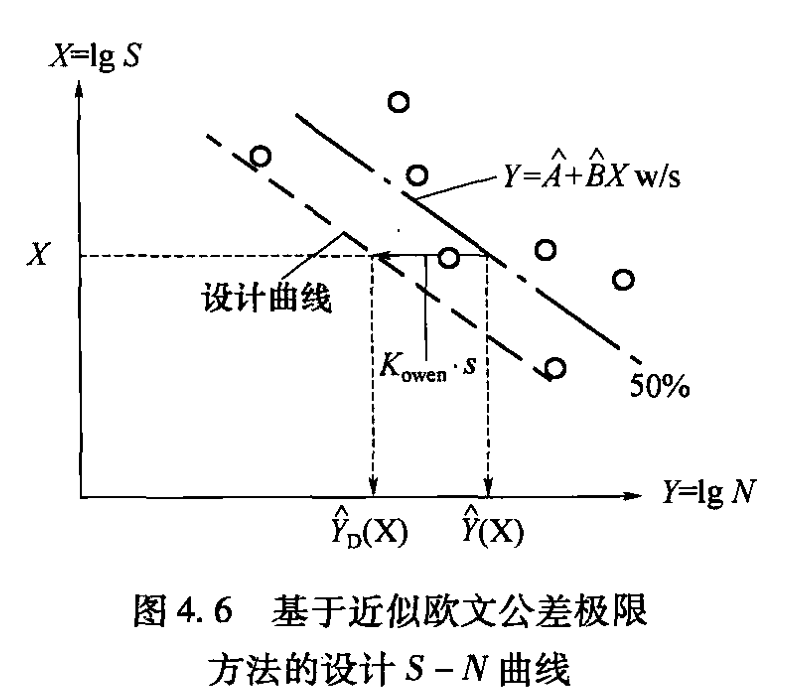
与后一种方法相比较,尽管STMA标准当时获得了较为广泛的应用和接受,但其仅为整个中值S-N曲线提供了一个确切的置信带,即R50值的双侧置信水平。另一方面,基于近似欧文公差极限方法推导出的单侧公差极限,对于任意可靠性值可灵活地获得下界置信水平。
1.2.1 ASTM法
双侧置信区间法,即ASTM法,考虑了附加变量X对K值的影响,其定义如下:
式中:\(F_{p,(2,n_s-2)}\)为具有(2, \(n_s\)-2)自由度的F分布值,预期置信区间为p,参见附录9.3 , python代码如下:
from scipy.stats import f;
p=0.9;n1=1;n2=1
f_val = f.ppf(q=p, dfn=n1, dfd=n2)
print(f_val)
由于ASTM标准用于生成双侧置信带,则必须有两个\(K_{\text{ASTM}}\)。将\(K_{\text{ASTM}}\)用于方程(4.2.16)时,对于上置信带\(K_{\text{ASTM}}\)取负值,对于下置信带取正值。应该注意到,\(n_s\)为样本容量。
1.2.2 单侧公差极限法
对于近似欧文单侧公差极限,K值由如下表达式推导出:
式中
其中
式中,下标R和C表示可靠性和置信水平,并且\(\varphi(\cdot)\)为标准的正态累积分布函数。
表4.3和表4.4列出了\(K_{\text{owen}}\)的经验系数。
图4.6中给出了说明这种方法的示意图。
表4.3 \(K_{\text{owen}}\)的经验系数\(b_i\)(\(i=1,2,3,4\))\(^{[40]}\)
| 置信水平(C) | \(b_1\) | \(b_2\) | \(b_3\) | \(b_4\) |
|---|---|---|---|---|
| 0.95 | 1.0908 | -0.1596 | 3.00 | -2.656 |
| 0.90 | 0.9968 | 0.0106 | 0.60 | 1.099 |
| 0.85 | 1.0010 | -0.7212 | 1.50 | -1.486 |
| 0.80 | 1.0010 | -0.6370 | 1.25 | -1.554 |
表4.4 \(K_{\text{owen}}\)经验系数\(c_i\)(\(i=1,2,3\))\(^{[40]}\)
| \(c_1\) | \(c_2\) | \(c_3\) | |
|---|---|---|---|
| \(f < 2\) | 1 | 1 | \(\frac{1}{3f}\) |
| \(f \geq 2\) | \(1 + \frac{3}{4(f-1.042)}\) | \(f-2\) | \(c_2 - c_1^2\) |
例4.3 确定样本容量为10、存活率为90%(R90)和置信水平为95%(C95)时的\(K_{\text{owen}}\)。
解:
表4.5列出了由威廉斯(Williams)等人2003年推导出的\(K_{\text{owen}}\)系数\(^{[51]}\),随着样本容量、可靠性水平和置信水平而变化,见附录4.2
2.数据案例
2.1 例4.2
根据例4.1中的工程结论,在可靠性开发时,对12个构件在\(R = -1\)加载条件下进行旋转弯曲疲劳试验。表4.2给出了有限寿命区域内的疲劳试验数据(附录4.1)。
- 利用最小二乘法确定S-N曲线,并将疲劳数据绘制在双对数坐标上。
- 将试验数据与预测的S-N曲线进行比较。同时确定统计疲劳特性。
- 说明S-N方程的限制条件。
解: 通过对表4.2第一、第二列中的应力幅和反向次数取以10为底的对数,来定义第三和第四列中的自变量(\(X\)和\(Y\))。采用最小二乘法,回归系数为
依据方程(4.2.11)、方程(4.2.12)和方程(4.2.15)
因此,S-N曲线的方程为
图4.4示出了在半对数坐标中预测中值S-N曲线与实验疲劳数据之间的比较。预测的S-N方程有如下限制:
(1) 仅对所给出的试验数据有效(即:有效寿命范围从\(9.8\times10^3\)到\(9.0\times10^7\)次反向)。
(2) 仅对旋转弯曲试验的相同失效模式有效。
(3) 具有代表性的中值疲劳数据。
(4) 假设\(N_f\)为对数正态分布。
(5) 对于所有的\(N_f\),\(N_f\)的离差被认为是常数。
2.2 例4.4
根据例4.2,具有50%可靠性(\(S'_f = 296\text{MPa}\)和\(b = -0.0377\))的S-N曲线确定为:
式中:\(S_a\)为名义应力幅。
问题:
(1) 已知样本容量为12,试样标准误差为0.4885,基于近似欧文公差极限方法,确定具有95%存活率(R95)和90%置信水平(C90)的下界S-N曲线。
(2) 基于ASTM标准E739,建立中值S-N曲线的95%置信区间。
解: (1) 将\(2N_f = 2\times10^6\)次反向输入到前面的方程中,确定应力幅\(S_a = 171\text{MPa}\)。
应该注意的是,中值S-N曲线上的这个点(\(S_a = 171, 2N_f = 2\times10^6\))是随意选择的。在双对数坐标中,具有R95C90的新设计曲线,可以通过将具有相同疲劳强度指数\(b = -0.0377\)的线由中值基准线水平左移\(K_{\text{ Owens}}\cdot s\)的距离来形成。查表4.5,样本容量为(\(n_s = 12\))、95%存活率和90%置信水平的\(K_{\text{ Owens}}\)系数为2.583。因此,R95C90疲劳寿命反向次数的对数,可以通过从中值疲劳寿命的对数中减去\(K_{\text{ Owens}}\cdot s\)的值来确定,即\(\lg(2N_{f,\text{R95,C90}}) = \lg(2\times10^6) - 2.583\times0.4885 = 5.309\)或
具有R95C90的S-N方程,可以通过相同斜率\(b\)、配对的\(S_a = 171\)和\(2N_{f,\text{R95,C90}} = 109400\)来确定。那么,疲劳强度系数\(S'_{f,\text{R95C90}}\)可以通过如下表达式来获得:
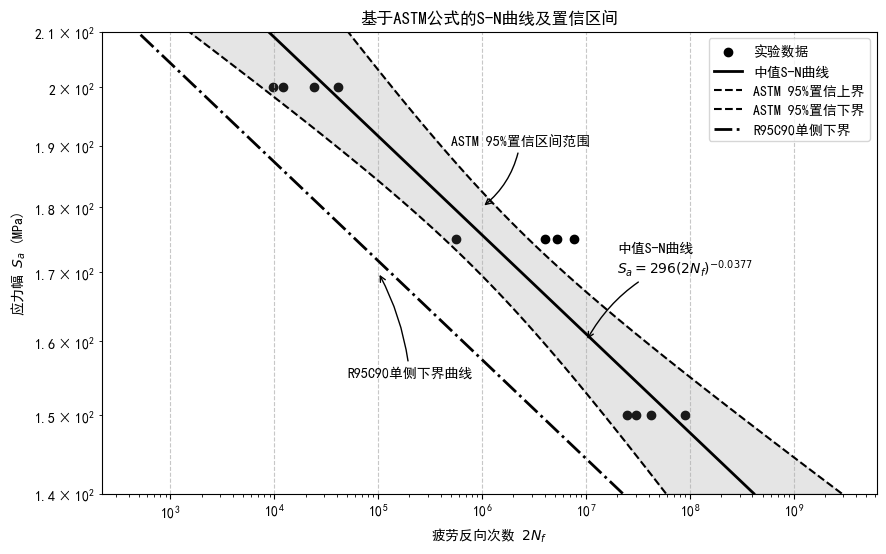
因此,如图4.4所示,具有R95C90的新S-N方程具有如下形式:
(2) 基于预期置信水平\(p = 0.95\)和样本容量\(n_s = 12\),在附录9.3中查找\((2, n_s - 2)\)自由度的\(F_{0.95}\)值。查出\(F_{0.95,(2,10)} = 4.10\)。此外,由表4.2还可查出\(\bar{X} = 2.24005\)和\(\sum_{i=1}^{n_s}(X_i - \bar{X})^2 = 0.031274\)。在计算绘制置信水平点的数据范围内,选择一系列\(X\)值。例如,在三个给定应力幅下,令\(X\)为2.30103、2.24304和2.17609。在选择的每个\(X\)值处,基于最小二乘回归线计算\(\hat{Y}\):
和方程(4.2.17)的\(K_{\text{ASTM}}\)。接着可以用下式来获得整条线的95%置信带:
最终,如图4.4所示,采用光滑曲线连接上部连续的三点和下部连续的三点,可以形成95%置信带。上界和下界分别表示具有R50C2.5和R50C97.5的曲线。
3.编程计算
3.8 \(K_{\text{owen}}\)系数计算
import numpy as np
from scipy import stats
# 定义置信水平C和存活率R的组合
C_list = [0.9, 0.95]
R_list = [0.90, 0.95, 0.99]
n_s_list = range(6, 31) # 样本容量n_s从6到30
# 表4.3的经验系数b1, b2, b3, b4(按C=0.95, 0.90, 0.85, 0.80顺序,这里取C=0.9和0.95对应的)
b_coeff = {
0.90: {'b1': 1.0030, 'b2': -6.0160, 'b3': 3.00, 'b4': 1.099},
0.95: {'b1': 0.9968, 'b2': 0.1596, 'b3': 0.60, 'b4': -2.636}
}
# 计算每个(n_s, C, R)对应的K_owen
def calculate_K_owen(n_s, C, R):
f = n_s - 2
a = 1.85 / n_s
K_R = stats.norm.ppf(R)
K_C = stats.norm.ppf(C)
# 计算c1, c2, c3(表4.4的公式)
if f < 2:
c1 = 1
c2 = 1
c3 = 1/(2*f)
else:
c1 = 1 + 3 / (4 * (f - 1.042))
c2 = f / (f - 2)
c3 = c2 - c1**2
# 计算K_D
K_D = c1 * K_R + K_C * np.sqrt(c3 * K_R**2 + c2 * a)
# 计算R_owen(表4.3的公式)
b = b_coeff[C]
R_owen = b['b1'] + b['b2'] / (f ** b['b3']) + b['b4'] * np.exp(-f)
# 计算K_owen
K_owen = K_D * R_owen
return K_owen
# 生成结果表格
print("n_s\tC=0.9,R=0.90\tC=0.9,R=0.95\tC=0.9,R=0.99\tC=0.95,R=0.90\tC=0.95,R=0.95\tC=0.95,R=0.99")
for n_s in n_s_list:
row = [str(n_s)]
for C in C_list:
for R in R_list:
k = calculate_K_owen(n_s, C, R)
row.append(f"{k:.3f}")
print('\t'.join(row))
4. 附录
4.1 疲劳试验数据
表4.2 零件S-N疲劳试验数据汇总
| 应力幅\(S_a/\text{MPa}\) | 疲劳寿命\(2N_f/\)反向次数 | \(\lg(S_a)\) | \(\lg(2N_f)\) | 应力幅\(S_a/\text{MPa}\) | 疲劳寿命\(2N_f/\)反向次数 | \(\lg(S_a)\) | \(\lg(2N_f)\) |
|---|---|---|---|---|---|---|---|
| 200 | \(9.8\text{E}+03\) | 2.30103 | 3.99123 | 175 | \(4.0\text{E}+06\) | 2.24304 | 6.60206 |
| 200 | \(1.2\text{E}+04\) | 2.30103 | 4.07918 | 175 | \(5.2\text{E}+06\) | 2.24304 | 6.71600 |
| 200 | \(4.1\text{E}+04\) | 2.30103 | 4.61278 | 150 | \(2.5\text{E}+07\) | 2.17609 | 7.39794 |
| 200 | \(2.4\text{E}+04\) | 2.30103 | 4.38021 | 150 | \(9.0\text{E}+07\) | 2.17609 | 7.95424 |
| 175 | \(7.7\text{E}+06\) | 2.24304 | 6.88469 | 150 | \(4.2\text{E}+07\) | 2.17609 | 7.63235 |
| 175 | \(5.6\text{E}+05\) | 2.24304 | 5.74819 | 150 | \(3.0\text{E}+07\) | 2.17609 | 7.47712 |
4.2 \(K_{\text{owen}}\)系数数值
表4.5 近似欧文公差极限的\(K_{\text{owen}}\)系数\(^{[51]}\)
| \(n_s\) | \(C=0.9\) | \(C=0.95\) | ||||
|---|---|---|---|---|---|---|
| \(R=0.90\) | \(R=0.95\) | \(R=0.99\) | \(R=0.90\) | \(R=0.95\) | \(R=0.99\) | |
| 6 | 2.862 | 3.504 | 4.750 | 3.560 | 4.331 | 5.837 |
| 7 | 2.608 | 3.190 | 4.319 | 3.167 | 3.846 | 5.173 |
| 8 | 2.441 | 2.987 | 4.043 | 2.910 | 3.534 | 4.751 |
| 9 | 2.323 | 2.843 | 3.851 | 2.728 | 3.314 | 4.455 |
| 10 | 2.253 | 2.736 | 3.707 | 2.592 | 3.151 | 4.237 |
| 11 | 2.162 | 2.651 | 3.595 | 2.485 | 3.024 | 4.069 |
| 12 | 2.105 | 2.583 | 3.505 | 2.400 | 2.923 | 3.936 |
| 13 | 2.057 | 2.526 | 3.430 | 2.331 | 2.840 | 3.827 |
| 14 | 2.016 | 2.478 | 3.367 | 2.272 | 2.771 | 3.737 |
| 15 | 1.980 | 2.436 | 3.313 | 2.222 | 2.712 | 3.660 |
| 16 | 1.949 | 2.400 | 3.266 | 2.178 | 2.661 | 3.594 |
| 17 | 1.922 | 2.369 | 3.225 | 2.140 | 2.617 | 3.536 |
| 18 | 1.898 | 2.340 | 3.189 | 2.106 | 2.577 | 3.485 |
| 19 | 1.876 | 2.315 | 3.156 | 2.076 | 2.542 | 3.440 |
| 20 | 1.857 | 2.292 | 3.127 | 2.048 | 2.510 | 3.399 |
| 21 | 1.839 | 2.272 | 3.100 | 2.024 | 2.482 | 3.363 |
| 22 | 1.822 | 2.252 | 3.076 | 2.001 | 2.456 | 3.329 |
| 23 | 1.807 | 2.235 | 3.054 | 1.981 | 2.432 | 3.300 |
| 24 | 1.793 | 2.219 | 3.034 | 1.961 | 2.410 | 3.271 |
| 25 | 1.781 | 2.204 | 3.015 | 1.947 | 2.389 | 3.247 |
| 26 | 1.769 | 2.191 | 2.997 | 1.927 | 2.370 | 3.221 |
| 27 | 1.757 | 2.178 | 2.981 | 1.912 | 2.353 | 3.199 |
| 28 | 1.747 | 2.166 | 2.966 | 1.898 | 2.337 | 3.178 |
| 29 | 1.737 | 2.155 | 2.952 | 1.885 | 2.321 | 3.158 |
| 30 | 1.728 | 2.144 | 2.939 | 1.872 | 2.307 | 3.140 |
4.3 完整代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import statsmodels.api as sm
# 1. 实验数据(表4.2)
S_a_exp = np.array([200, 200, 200, 200, 175, 175, 175, 175, 150, 150, 150, 150])
N2f_exp = np.array([9.8e3, 1.2e4, 4.1e4, 2.4e4, 7.7e6, 5.6e5, 4.0e6, 5.2e6,2.5e7,
9.0e7, 4.2e7, 3.0e7])
# 2. 对数转换(核心变量定义)
X = np.log10(S_a_exp) # 自变量 X = lg(S_a)
Y = np.log10(N2f_exp) # 因变量 Y = lg(2N_f),满足 Y = A + B·X
n_s = len(X) # 样本量
X_mean = np.mean(X) # X的均值
SS_xx = np.sum((X - X_mean)**2) # 总偏差平方和:Σ(X_i - X̄)²
# 3. 线性回归(获取A、B和残差标准差)
X_with_const = sm.add_constant(X)
model = sm.OLS(Y, X_with_const)
results = model.fit()
A, B = results.params # 回归系数:Y = A + B·X
sigma_hat = np.sqrt(results.mse_resid) # 残差标准差 s
df = results.df_resid # 自由度 = n_s - 2
# 4. 中值S-N曲线计算
S_a_range = np.logspace(np.log10(140), np.log10(210), 100) # 应力幅范围
lg_Sa_range = np.log10(S_a_range) # X_i = lg(S_a)
Y_median = A + B * lg_Sa_range # 中值对数值:lg(2N_f) = A + B·lg(S_a)
N2f_median = 10 ** Y_median # 中值曲线:2N_f
# 5. ASTM置信区间计算(基于公式 K_{\text{ASTM}})
p = 0.95 # 置信水平
F_val = stats.f.ppf(p, dfn=2, dfd=df) # F分布分位数 F_{p,(2, n_s-2)}
# 严格按照公式计算 K 值(包含符号逻辑)
K_term = np.sqrt(2 * F_val) * np.sqrt( (1/n_s) + (lg_Sa_range - X_mean)**2 / SS_xx )
K_upper = -K_term # 上界修正系数(对应较小的2N_f)
K_lower = +K_term # 下界修正系数(对应较大的2N_f)
# 计算置信区间对数值
Y_upper = Y_median + K_upper * sigma_hat # lg(2N_f)上界
Y_lower = Y_median + K_lower * sigma_hat # lg(2N_f)下界
# 转换回原尺度
N2f_upper = 10 ** Y_upper
N2f_lower = 10 ** Y_lower
# 6. 欧文单侧公差极限(R95C90)
R, C = 0.95, 0.90
b1, b2, b3, b4 = 1.0030,-6.0160,3.00,1.099
f = n_s - 2
a = 1.85 / n_s
K_R = stats.norm.ppf(R)
K_C = stats.norm.ppf(C)
c1 = 1 + 3 / (4 * (f - 1.042))
c2 = f / (f - 2)
c3 = c2 - c1**2
K_D = c1 * K_R + K_C * np.sqrt(c3 * K_R**2 + c2 * a)
R_owen = b1 + b2 / (f ** b3) + b4 * np.exp(-f)
K_owen = K_D * R_owen
# K_owen=2.583
Y_owen = Y_median - K_owen * sigma_hat # 单侧下界对数值
N2f_owen = 10 ** Y_owen
# 7. 绘图验证
plt.figure(figsize=(10, 6))
plt.scatter(N2f_exp, S_a_exp, color='black', label='实验数据')
plt.plot(N2f_median, S_a_range, 'k-', linewidth=2, label='中值S-N曲线')
plt.plot(N2f_upper, S_a_range, 'k--', label='ASTM 95%置信上界')
plt.plot(N2f_lower, S_a_range, 'k--', label='ASTM 95%置信下界')
plt.plot(N2f_owen, S_a_range, 'k-.', linewidth=2, label='R95C90单侧下界')
plt.fill_betweenx(S_a_range, N2f_lower, N2f_upper, color='gray', alpha=0.2)
plt.xscale('log')
plt.yscale('log')
plt.xlabel('疲劳反向次数 $2N_f$')
plt.ylabel('应力幅 $S_a$ (MPa)')
plt.ylim(140, 210)
plt.legend()
plt.grid(ls='--', alpha=0.7)
plt.title('基于ASTM公式的S-N曲线及置信区间')
# 给三条关键曲线添加指示说明
plt.annotate('中值S-N曲线\n$S_a=296(2N_f)^{-0.0377}$',
xy=(1e7, 160), xytext=(1e7*2, 170),
arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.2'))
plt.annotate('ASTM 95%置信区间范围',
xy=(1e6, 180), xytext=(1e6*0.5, 190),
arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=-0.2'))
plt.annotate('R95C90单侧下界曲线',
xy=(1e5, 170), xytext=(1e5*0.5, 155),
arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.1'))
plt.show()
5. 参考文献
[2] American Society for Testing and Materials (ASTM), Standard practice for statistical analysis of linear or linearized stress – life (S – N) and strain – life (e – N) fatigue data, ASTM Standard, E739 – 91, West Conshohocken, PA, 1998, pp. 631 – 637.
[24] Lieberman, G. J., Tables for one – sided statistical tolerance limits, Industrial Quality Control, Vol. XIV, No. 10, 1958, pp.7 – 9.
[40] Shen, C. L., Wirshing, P. H., and Cashman, G. T., Design curve to characterize fatigue strength, Journal of Engineering Materials and Technology, Vol. 118, 1996, pp. 535–541.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号