3.1 几个基本概念
• 外力
外力指的是我们熟知的机械力、电磁力等,物体因外力作用而变形。作用于物体的外力可分为体积力和表面 力,它们分别简称为体力和面力。
体力是分布在物体体积内的力,例如重力和惯性力。一般来说,物体内各点所受体力是各不相同的。
面力 是分布在物体表面上的力,如流体压力和接触力等。物体内各点所受面力一般也是各不相同的。
为了表述物体表面某一点 P 所受面力的大小和方向,取包含点 P 的一微小表面区域,它的面积为\(\Delta s\) 。设作 用于上的面力为$ \overrightarrow {\Delta T} $ , 则称 $ \overrightarrow {\Delta T} / \Delta S$为 面力的平均集度 。设面力为连续分布,命 无限减小而趋于点 P P ,则 $ \overrightarrow {\Delta T} / \Delta S$ 将趋于一极限,即
\[\vec{P}=\lim_{\Delta S\to0}\frac{\overline{\Delta T}}{\Delta S}=T_{i}\vec{i}_{i}=T_{x}\vec{i}+T_{y}\vec{j}+T_{z}\vec{k}
\]
式中 \(T_x,T_y,T_z\) 为面力沿三个坐标轴分量。规定面力沿三个坐标轴分量与坐标轴的正向相同时为正,反之为 负。
物体由于外力的作用,内部将产生抵抗外力的力,即 内力 。通常用 应力 这个概念来描述内力的大小。
物体内一点 P 的 全应力 定义为:
\[\vec{p}=\lim_{\Delta S\to0}\frac{\overrightarrow{\Delta P}}{\Delta S}
\]
通常,我们 将全应力分解成两个分量 :一个是沿截面法线 v 方向,该方向的分量称为 正应力 并用\(\sigma\) 表示; 另 一个是位于截面上的分量,称为 剪应力( ( 或切应力) ) 用\(\tau\)表示。
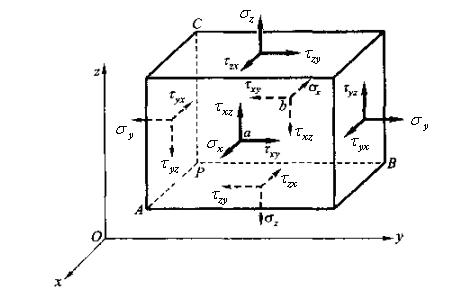
3.2 一点的应力状态与应力张量• 点 P 的应力与通过该点的截面方位相关,通过点 P 的截面不同,按定义所确 定的应力也将不同。要确定点 P 的应力,需要确定过点 P 所有截面上的应力。• 一点的应力状态就是指通过物 体内一点的所有截面上的应力集合。
为确定一点的应力状态,通过该点截取一个微小的正六面体,研究表明:只要该正六面体六个面上的应力已 知,过该点其它任意方向截面上的应力均可以确定下来。
正应力和剪应力的表示,例如\(\sigma_x\tau_{xy}\)
正应力与剪应力的正负号规定 :
如果某一个截面的外法线方向与坐标轴的正方向一致,这个截面称为 正面 , 正面上的应力正负号规定为与坐 标轴的正方向一致时为正,反之为负;相反,如果某一个截面的外法线方向与坐标轴的正方向反向,这个截 面称为 负面 , 负面上的应力正负号规定。
![image-20240721005131414]()
描述一点应力状态的九个应力分量
\[\sigma_x,\quad\tau_{xy},\quad\tau_{xz},\quad\sigma_y,\quad\tau_{yx},\quad\tau_{yz},\quad\sigma_z,\quad\tau_{zx},\quad\tau_{zy}
\]
可用矩阵形式表达为
\[\begin{bmatrix}\sigma_x&\tau_{xy}&\tau_{xz}\\\tau_{yx}&\sigma_y&\tau_{yz}\\\tau_{zx}&\tau_{zy}&\sigma_z\end{bmatrix} \implies \begin{bmatrix}\sigma_{xx}&\tau_{xy}&\tau_{xz}\\\tau_{yx}&\sigma_{yy}&\tau_{yz}\\\tau_{zx}&\tau_{zy}&\sigma_{zz}\end{bmatrix} \implies \begin{bmatrix}\sigma_{xx}&\sigma_{xy}&\sigma_{xz}\\\sigma_{yx}&\sigma_{yy}&\sigma_{yz}\\\sigma_{zx}&\sigma_{zy}&\sigma_{zz}\end{bmatrix}
\]
采用张量下标记号,可表示成
\[\left(\sigma_{ij}\right)=\left(\begin{array}{ccc}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{21}&\sigma_{22}&\sigma_{23}\\\sigma_{31}&\sigma_{32}&\sigma_{33}\end{array}\right)
\]
研究表明,\(\sigma_{ij}\) 的九个分量构成二阶张量,我们称之为应力张量
六个剪应力并不都是独立的,它们之间具有一定的互等关系。
\[\tau_{yz}=\tau_{zy}\quad\tau_{zx}=\tau_{xz}\quad\tau_{xy}=\tau_{yx}
\]
剪应力之间的这种两两相等的关系,称为剪应力互等定理。
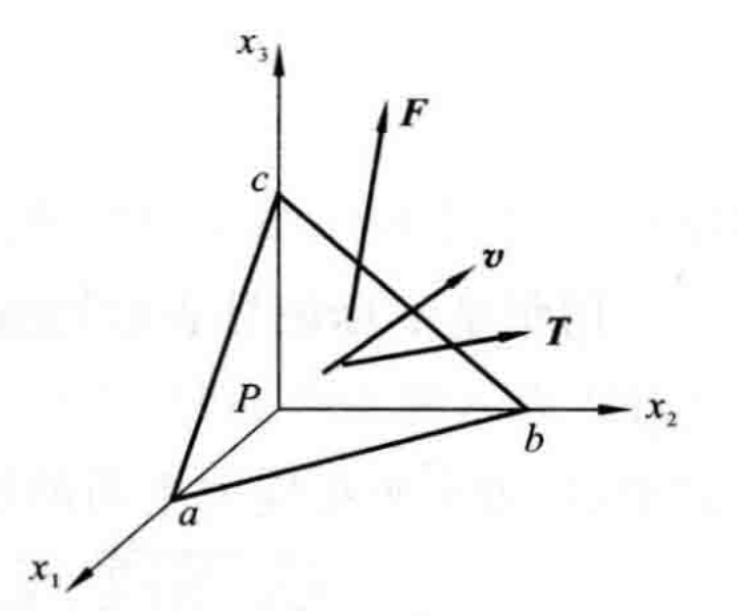
3.3 任意斜截面上的应力
设通过点 P 并平行于坐标面的三个微分面上的应力为巳知,现在来确定通过该点的某一斜微分面上的应力点 P 附近取一斜微分面 abc ,其外法线 v 与各坐标轴的方向余弦为:
\[\cos(\vec{\nu},x)=l\\\cos(\vec{\nu},y)=m\\\cos(\vec{\nu},z)=n
\]
![image-20240721005829863]()
列出 x 、y 和 z 三个方向上的平衡方程可得
\[T_{x}=\sigma_{x}l+\tau_{xy}m+\tau_{xz}n\\T_{y}=\tau_{yx}l+\sigma_{y}m+\tau_{yz}n\\T_{x}=\tau_{zx}l+\tau_{zy}m+\sigma_{z}n
\]
采用张量下标记号法,有
\[T_i=\sigma_{ij}l_j
\]
根据张量判别定理,即知 \(\sigma_{ij}\) 为二阶张量.
将\(T_x\)、\(T_y\)和\(T_z\)投影到法线\(\nu\)上,可得斜微分面上的正应力为:
\[\begin{aligned}
&\sigma_\nu=T_xl+T_ym+T_zn \\
&=\sigma_{x}l^{2}+\sigma_{y}m^{2}+\sigma_{z}n^{2}+2\tau_{xy}lm+2\tau_{yz}mn+2\tau_{zx}nl
\end{aligned}
\]
斜微分面上的剪应力由下式求出
\[\tau_\nu^2=(T_x^2+T_y^2+T_z^2)-\sigma_\nu^2
\]
3.4 主应力及应力(张量)不变量
若经过物体内某点的某一个斜截面上的剪应力等于零,则该斜截面上的正应力称为该点的一个主应力,该面称为该点的一个应力主面,该面的法线方向称为该点的一个应力主向。
现在取物体内任意一点例如点 P 来研究。设点 P 有一个应力主面存在,则在该应力主面上剪应力为零,该面上的全应力就应等于该面上的正应力,用\(\sigma\) 表示该面上的正应力,有:
\[\begin{aligned}
&\sigma l=\sigma_xl+\tau_{xy}m+\tau_{xz}n \\
&\sigma m=\tau_{yx}l+\sigma_{y}m+\tau_{yz}n \\
&\sigma n=\tau_{zx}l+\tau_{zy}m+\sigma_zn
\end{aligned}
\]
\[\boxed{T_{x}=\sigma_{x}l+\tau_{xy}m+\tau_{xz}n\\T_{y}=\tau_{yx}l+\sigma_{y}m+\tau_{yz}n\\T_{x}=\tau_{zx}l+\tau_{zy}m+\sigma_{z}n}
\]
用张量下标记号表示,上式可表示成:
\[\begin{aligned}(\sigma_{ij}-\sigma\delta_{ij})l_j&=0&\text{(a)}\\\textbf{另有:}\quad l_il_i&=1&\text{(b)}\end{aligned}
\]
满足式 (b) 的条件,求式 (a) 的非全零解,则式 (a)的系数行列式必须等于零,即
\[\left.\left|\begin{array}{ccc}\sigma_{11}-\sigma&\sigma_{21}&\sigma_{31}\\\sigma_{12}&\sigma_{22}-\sigma&\sigma_{32}\\\sigma_{13}&\sigma_{23}&\sigma_{33}-\sigma\end{array}\right.\right|=0
\]
展开上式得的三次方程:
\[\sigma^3-J_1\sigma^2-J_2\sigma-J_3=0
\]
\[\begin{aligned}
&J_{1} =\sigma_{11}+\sigma_{22}+\sigma_{33}=\sigma_{x}+\sigma_{y}+\sigma_{z}=\sigma_{kk} \\
&J_{2} =-\sigma_x\sigma_y-\sigma_y\sigma_z-\sigma_z\sigma_x+\tau_{xy}^2+\tau_y^2 =-\begin{vmatrix}\sigma_{11}&\sigma_{12}\\\sigma_{21}&\sigma_{22}\end{vmatrix}-\begin{vmatrix}\sigma_{22}&\sigma_{23}\\\sigma_{32}&\sigma_{33}\end{vmatrix}-\begin{vmatrix}\sigma_{33}&\sigma_{31}\\\sigma_{13}&\sigma_{11}\end{vmatrix} & \\
&=-\frac12(\sigma_{ii}\sigma_{kk}-\sigma_{ik}\sigma_{ki}) \\
&J_{3} =\begin{vmatrix}\sigma_{11}&\sigma_{12}&\sigma_{13}\\
\sigma_{21}&\sigma_{22}&\sigma_{23}\\
\sigma_{31}&\sigma_{32}&\sigma_{33}\end{vmatrix}=\epsilon_{ijk} \sigma_{i1}\sigma_{j2}\sigma_{k3}
\end{aligned}
\]
\(J_{1}、J_{2}\)和\(J_{2}\)为应力或应力张量的三个不变量
研究表明,一点有三个主应力,对应也就有三个应力主面和三个应力主向。用\(\sigma_1\)、\(\sigma_2\)和\(\sigma_3\)表示三个主应力,\(\vec{n}_1\) 、\(\vec{n}_2\) 和\(\vec{n}_3\)表示它们对应的主方向,有:
(1) 当\(\sigma_1\neq\sigma_2\neq\sigma_3\)时,\(\vec{n}_1\perp\vec{n}_2,\vec{n}_2\perp\vec{n}_3,\vec{n}_3\perp\vec{n}_1\)
(2) 当有一个重根时,如 \(\sigma _1= \sigma _2\neq \sigma _3\) ,则法线与 \(\vec{n}_3\)垂直的平面上的所有正应力方向均为应力主方向,且所有这些平面上正应力或主应力\(\sigma\) 为一常量,\(\sigma=\sigma_1=\sigma_2;\)
(3)当\(\sigma_1=\sigma_2=\sigma_3\),任意方向均为主方向,这种应力状态称为球应力或静水应力状态。
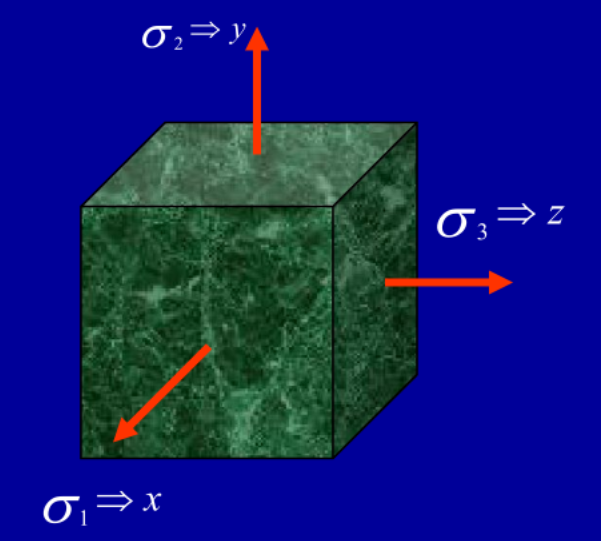
3.5 最大、最小正应力和最大剪应力
将坐标轴的方向设置成与一点的三个主应力方向相同,三个主应力用\(\sigma_1、\sigma_2\)、和 \(\sigma_3\) 表示,轴x对应 \(\sigma_1\), 轴y对应 \(\sigma_2\),轴z对应 $\sigma_3 $,
![image-20240721011558416]()
\[
\]
参考文献:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号