题解 Frog 3

题目描述

将一个序列分成若干段，每一段的价值为 \((h_i-h_j)^2+C\)，求价值和的最小值。

具体思路

设 \(f_i\) 表示前 \(i\) 个数分成若干段的价值和的最小值，并且 \(j+1 \sim i\) 被分成了一段。

那么 \(f_i\) 的状态应该由 \(f_j\) 转移过来。

状态转移方程：

\[f_i=\min \limits_{0 \le j<i} \{ {f_j+(h_i-h_j)^2+C} \} \]

形如：

\[f_i=\min \limits_{0 \le j<i} \{ {f_j+val} \} \]

这一类动态规划的优化分为三种：单调队列，斜率优化，四边形不等式。

而这几种优化方式对应的状态转移方程是不同的。

单调队列：单调队列对应的 \(val\) 一般是一次的，这题不符合。

斜率优化：斜率优化对应的 \(val\) 一般是二次的，这题符合。

四边形不等式：四边形不等式对应的 \(val\) 需要满足四边形不等式。

我们现在面临选择斜率优化还是四边形不等式优化。显然斜率优化的时间复杂度 \(O(n)\) 是要优于四边形不等式的时间复杂度 \(O(n \log n)\) 的，因此我们考虑斜率优化。

这里考虑将状态转移方程式化为截距式：\(b=y-kx\)。

\[f_i-C=\min \limits_{0 \le j<i} \{ {f_j+h_i^2+h_j^2-2h_ih_j} \} \]

\[f_i-h_i^2-C=\min \limits_{0 \le j<i} \{ {f_j+h_j^2-2h_ih_j} \} \]

令 \(b=f_i-h_i^2-C\)，\(y=f_j+h_j^2\)，\(k=2h_i\)，\(x=h_j\)。

由于题目中说 \(h_i\) 单调递增，这里的斜率 \(k\) 应该是单调递增的，因此维护下凸壳。

那么我们该怎么维护呢？

我们说了，斜率是单调的，那么自然就想到用单调队列维护下凸壳。

显然，我们每次的最优决策点，即让截距 \(b\) 取到的最小值的点 \(j\)，应当满足它左边的斜率小于当前的斜率，右边的斜率大于当前的斜率。

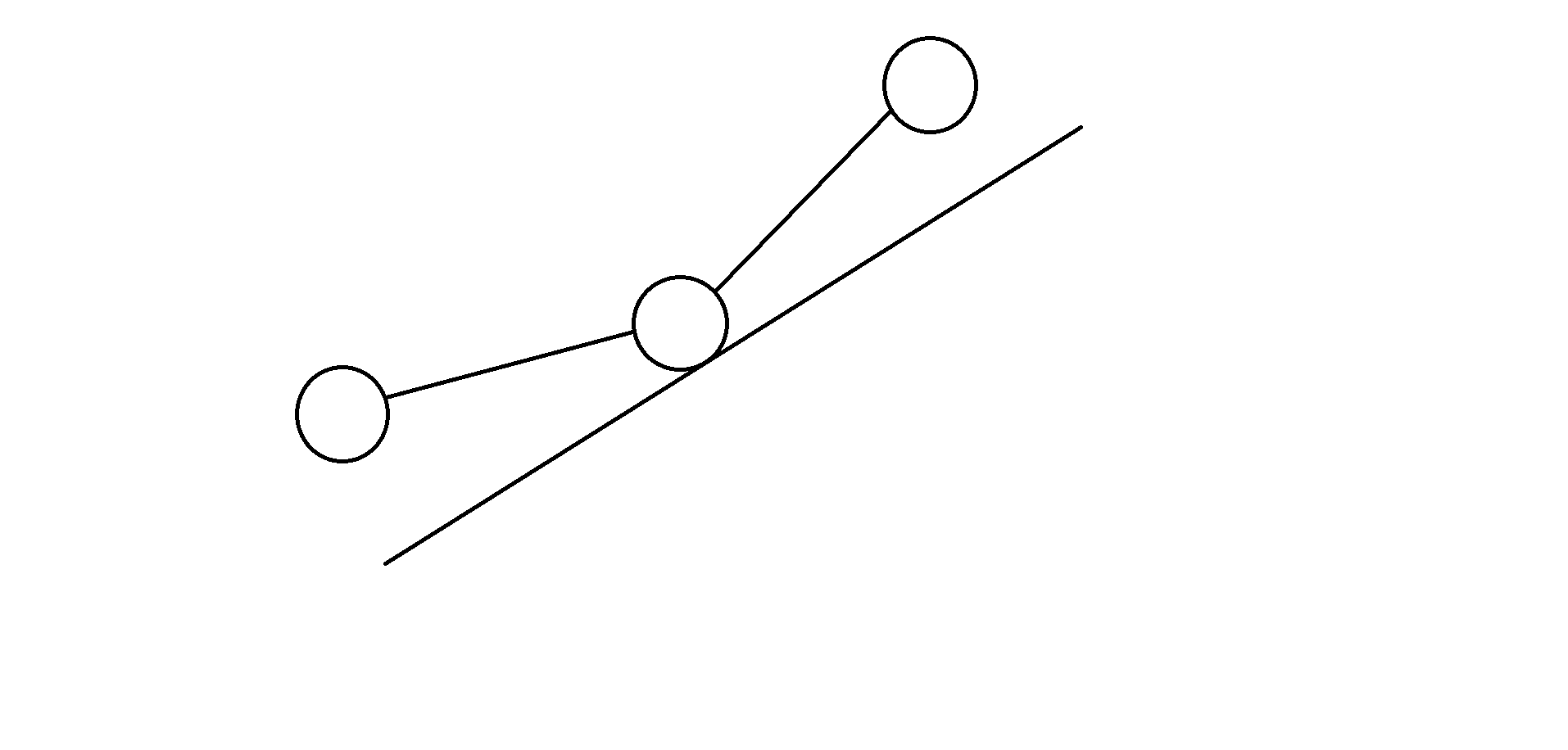
因此我们取队头时应当将所有斜率小于等于 \(k\) 的点全部踢出单调队列。

然后我们在队尾维护单调队列的斜率单调递增，即每次将斜率比当前直线斜率大的踢出单调队列。

注意

青蛙一开始站在第一块石头上，因此 dp 要从 \(2\) 开始。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=211000;
LL h[N],f[N];
int l,r,Q[N];
double X(int j){return 1.0*h[j];}
double Y(int j){return 1.0*(f[j]+h[j]*h[j]);}
double slop(int j1,int j2){
	if(X(j2)==X(j1))return 1e18;
	return (Y(j2)-Y(j1))/(X(j2)-X(j1));
}
int main(){
	int n;LL c;scanf("%d%lld",&n,&c);
	for(int i=1;i<=n;i++){
		scanf("%lld",&h[i]);
	}
	memset(f,0x3f,sizeof(f));
	f[1]=0;
	l=1,r=1,Q[l]=1;
	for(int i=2;i<=n;i++){
		while(l<r&&slop(Q[l],Q[l+1])<=2.0*h[i])l++;
		int j=Q[l];
		f[i]=f[j]+(h[i]-h[j])*(h[i]-h[j])+c;
		while(l<r&&slop(Q[r-1],Q[r])>=slop(Q[r],i))r--;
		Q[++r]=i;
	}
	printf("%lld",f[n]);
	return 0;
}