题解 P2674 《瞿葩的数字游戏》T2-多边形数

题目描述

给你一个正整数数 \(n\)，问你它是不是多边形数 \(K\)，如果是，设 \(K_1\) 是最小的 \(K\)，\(K_2\) 是次小的 \(K\)，输出 \(K_1\) 和 \(K_2\)。

具体思路

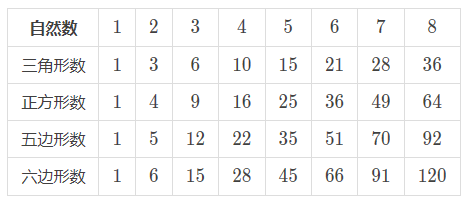
我们主要来看上面这张表里有什么规律。

• 性质 1：\(1\) 是任何一个多边形数。

• 性质 2：\(2\) 不是任何一个多边形数。

• 性质 3：除了 \(1\) 和 \(2\) 以外任意的正整数 \(n\) 都是一个 \(n\) 边形数。

• 性质 4：初中数学老师告诉过我，对于一个数列里的相邻两项关系一般满足函数关系。因此我们来看看相邻两项之间的变化量。

三角形数： \(2,3,4,5 \ldots\)，

四边形数： \(3,5,7,9 \ldots\)，

五边形数： \(4,7,10,13 \ldots\)，

六边形数： \(5,9,13,17 \ldots\)，

我们发现这些变化量之间的差是相同的，是一个等差数列，那也就是满足一次函数关系。

三角形数： \(y=x+1\)，

四边形数： \(y=2x+1\)，

五边形数： \(y=3x+1\)，

六边形数： \(y=4x+1\)，

因此对于任意的正整数 \(n\)，变化量满足一次函数关系：\(y=(n-2)x+1\)，其中 \(n>2\)。

那我们有了变化量之间的关系，就可以来表示上表中的任意一个数。

设我们求的是 \(n\) 边形数中的第 \(m\) 个数 \(x\)。

\[x=1+\sum_{i=1}^{m-1}((n-2) \times i+1) \]

\[x=1+(m-1) +\sum_{i=1}^{m-1}(n-2) \times i \]

\[x=m +(n-2) \times \sum_{i=1}^{m-1} i \]

\[x=m +(n-2) \times \frac{m(m-1)}{2} \]

\[x=m \times (1+\frac{(n-2)(m-1)}{2}) \]

我们将每次询问的数 \(x\) 拆成两个数相乘的形式，那我们枚举 \(x\) 的每个因数 \(m\) 不就完了吗？

你先别急，我们来看样例。

样例中，\(x=36,n=3,m=8\)。

然后惊人的发现 \(8\) 居然不是 \(36\) 的因数，是我们式子推错了吗？

别急着把草稿擦掉，我们来思考为什么会这样。

原因就是一开始我们计算等差数列的和时，我们是除以了一个 \(2\)，然而这个 \(2\) 有可能是 \(m\) 给的，因此我们直接将 \(m\) 提出来就会导致里面那坨东西是一个分数。

那我们怎么办啊？简单，去分母呗，即等式两边同时乘以一个 \(2\)。

\[2x=m \times 2 \times (1+\frac{(n-2)(m-1)}{2}) \]

\[2x=m \times (2+(n-2)(m-1)) \]

那么现在就可以放心大胆的去枚举 \(2x\) 的因数 \(m\) 了。

由于题目求的是最小的 \(n\)，因此我们要从大到小开始枚举 \(m\)。

时间复杂度：\(O(T \sqrt n)\)

注意

• 别忘了我们一开始推出来的性质 1 和性质 2，要记得特判。

• 由于我们枚举因数只枚举到 \(\sqrt x\)，因此有可能不满两个多边形数，这时候要用上性质 3，直接输出 \(x\)。

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
	int t;scanf("%d",&t);
	while(t--){
		int n;scanf("%d",&n);
		if(n==1){
			puts("3 4");
			continue;
		}
		if(n==2){
			puts("Poor2");
			continue;
		}
		int ans=0,res=0;
		n=n*2;
		for(int i=sqrt(n);i>=3;i--){
			if(n%i==0){
				if((n/i-2)%(i-1)==0){
					if(!ans)ans=(n/i-2)/(i-1)+2;
					else if(!res){
						res=(n/i-2)/(i-1)+2;
						break;
					}
				}
			}
		}
		if(ans&&res){
			printf("%d %d\n",ans,res);
		}
		if(ans&&!res){
			printf("%d %d\n",ans,n/2);
		}
		if(!ans){
			printf("%d\n",n/2);
		}
	}
	return 0;
}