题解 P8670 [蓝桥杯 2018 国 B] 矩阵求和

题目描述

$$\sum _{i=1}^n\sum _{j=1}^{n}gcd(i,j{)}^2$$

具体思路

solution 1

显然可以每次枚举 $gcd(i,j)$ 的取值。

$$\sum _{k=1}^n{k}^2\sum _{i=1}^n\sum _{j=1}^n[gcd(i,j)=k]$$

令 $i=\lfloor \frac{i}{k}\rfloor$，$j=\lfloor \frac{j}{k}\rfloor$。

$$\sum _{k=1}^n{k}^2\sum _{i=1}^{\lfloor \frac{n}{k}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{k}\rfloor }[gcd(i,j)=1]$$

$$\sum _{k=1}^n{k}^2\sum _{i=1}^{\lfloor \frac{n}{k}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{k}\rfloor }\epsilon (gcd(i,j))$$

然后进行莫比乌斯反演。

$$\sum _{k=1}^n{k}^2\sum _{i=1}^{\lfloor \frac{n}{k}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{k}\rfloor }\sum _{d\mid gcd(i,j)}\mu (d)$$

$$\sum _{k=1}^n{k}^2\sum _{i=1}^{\lfloor \frac{n}{k}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{k}\rfloor }\sum _{d\mid i,d\mid j}\mu (d)$$

交换求和顺序，由于先枚举 $i,j$ 再枚举 $d$，此时 $d$ 是 $i,j$ 的约数，因此反过来先枚举 $d$ 再枚举 $i,j$，此时 $i,j$ 就是 $d$ 的倍数。而 $1\sim \lfloor \frac{n}{k}\rfloor$ 里面 $d$ 的倍数有 $\lfloor \frac{n}{kd}\rfloor$ 个。

$$\sum _{k=1}^n{k}^2\sum _{d=1}^{\lfloor \frac{n}{k}\rfloor }\mu (d)\sum _{i=1}^{\lfloor \frac{n}{kd}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{kd}\rfloor }1$$

$$\sum _{k=1}^n{k}^2\sum _{d=1}^{\lfloor \frac{n}{k}\rfloor }\mu (d)\lfloor \frac{n}{kd}\rfloor \lfloor \frac{n}{kd}\rfloor$$

令：

$$f(n)=\sum _{d=1}^n\mu (d)\lfloor \frac{n}{d}\rfloor \lfloor \frac{n}{d}\rfloor$$

有：

$$\sum _{k=1}^n{k}^{2}f(\lfloor \frac{n}{k}\rfloor )$$

显然 $f(n)$ 可以数论分块解决，而最后的式子也可以数论分块解决，即数论分块套数论分块。

时间复杂度

$$O(\sum _{i=1}^{\sqrt{n}}\sqrt{\frac{n}{i}})=O(\sqrt{n}{\int }_0^{\sqrt{n}}{i}^{-\frac{1}{2}})=O(n^{\frac{3}{4}})$$

这个复杂度跑 $1e7$ 还是挺轻松的，但是不知道为什么题解区其他人竟然跑成了 $O(n\ln n)$

注意

平方和公式：$$\sum _{i=1}^n{i}^2=\frac{n\times (n+1)\times (2n+1)}{6}$$

由于要对 $1e9+7$ 取模，因此要记得及时取模，不然会 WA。

同时数论分块的时候，用平方和公式要记得乘 $6$ 的逆元。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e7;
const int mod=1e9+7;
int v[N+5],prime[N+5],pr;
int mu[N+5];LL sum[N+5];
LL qpow(LL a,LL b){
	LL ans=1%mod;a%=mod;
	while(b){
		if(b&1)ans=ans*a%mod;
		a=a*a%mod;b>>=1;
	}
	return ans;
}
void init(int n){
	memset(v,0,sizeof(v));pr=0;
	mu[1]=1;
	for(int i=2;i<=n;i++){
		if(!v[i]){
			prime[++pr]=i;
			mu[i]=-1;
		}
		for(int j=1;j<=pr&&i*prime[j]<=n;j++){
			v[i*prime[j]]=1;
			if(i%prime[j]==0){
				mu[i*prime[j]]=0;
				break;
			}
			mu[i*prime[j]]=-mu[i];
		}
	}
	for(int i=1;i<=n;i++){
		sum[i]=(sum[i-1]+mu[i])%mod;
	}
}
LL block(LL n){
	LL ans=0;
	for(LL l=1,r=0;l<=n;l=r+1){
		r=n/(n/l);
		ans=(ans+(sum[r]-sum[l-1])%mod*(n/l)%mod*(n/l)%mod+mod)%mod; 
	}
	return ans;
}
LL f(LL n){
	return n*(n+1)%mod*(2*n+1)%mod*qpow(6,mod-2)%mod;
}
LL calc(LL n){
	LL ans=0;
	for(LL l=1,r=0;l<=n;l=r+1){
		r=n/(n/l);
		ans=(ans+(f(r)-f(l-1))%mod*block(n/l)%mod+mod)%mod;
	}
	return ans;
}
int main(){
	LL n;scanf("%lld",&n);
	init(n);
	printf("%lld\n",calc(n));
	return 0;
}

solution2

我们回到这个式子：

$$\sum _{k=1}^n{k}^2\sum _{i=1}^{\lfloor \frac{n}{k}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{k}\rfloor }[gcd(i,j)=1]$$

我们考虑：

$$\sum _{i=1}^n\sum _{j=1}^n[gcd(i,j)=1]$$

我们运用数形结合的思想，把这个东西看作是平面上有 $n^2$ 个点，然后让你求这些点中横坐标与纵坐标互质的点的个数，这东西不是 P2158 [SDOI2008] 仪仗队 吗？

这个时候我们使用几何直观，沿着对角线把这些点分成两部分。

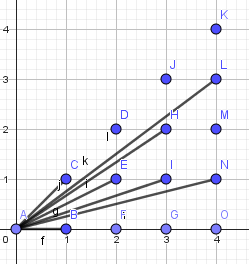
那么式子就变成了：

$$\sum _{i=1}^n\sum _{j=1}^i[gcd(i,j)=1]$$

显然另一部分是对称的，同时要减去算了两遍的 $(1,1)$，即：

$$2\times \sum _{i=1}^n\sum _{j=1}^i[gcd(i,j)=1]-1$$

根据欧拉函数的定义，有：

$$2\times \sum _{i=1}^n\phi (i)-1$$

把这个式子带回去，有：

$$\sum _{k=1}^n{k}^2\times (2\times \sum _{i=1}^{\lfloor \frac{n}{k}\rfloor }\phi (i)-1)$$

令：

$$f(n)=2\times \sum _{i=1}^n\phi (i)$$

有：

$$\sum _{k=1}^n{k}^2(f(\lfloor \frac{n}{k}\rfloor )-1)$$

显然可以数论分块做。

时间复杂度

只用跑一次数论分块，时间复杂度为：$O(\sqrt{n})$。

不过题解区又是让我很迷的做法，竟然不用数论分块而是用暴力 $O(n)$。

注意

平方和公式：$$\sum _{i=1}^n{i}^2=\frac{n\times (n+1)\times (2n+1)}{6}$$

由于要对 $1e9+7$ 取模，因此要记得及时取模，不然会 WA。

同时数论分块的时候，用平方和公式要记得乘 $6$ 的逆元。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e7;
const int mod=1e9+7;
int v[N+5],prime[N+5],pr;
int phi[N+5];LL sum[N+5];
LL qpow(LL a,LL b){
	LL ans=1%mod;a%=mod;
	while(b){
		if(b&1)ans=ans*a%mod;
		a=a*a%mod;b>>=1;
	}
	return ans;
}
void init(int n){
    memset(v,0,sizeof(v));pr=0;
    phi[1]=1;
    for(int i=2;i<=n;i++){
        if(!v[i]){
            prime[++pr]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=pr&&i*prime[j]<=n;j++){
            v[i*prime[j]]=1;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
    for(int i=1;i<=n;i++){
    	sum[i]=(sum[i-1]+phi[i])%mod;
	}
	for(int i=1;i<=n;i++){
		sum[i]=sum[i]*2%mod;
	}
}
LL f(LL n){
	return n*(n+1)%mod*(2*n+1)%mod*qpow(6,mod-2)%mod;
}
LL block(LL n){
	LL ans=0;
	for(LL l=1,r=0;l<=n;l=r+1){
		r=n/(n/l);
		ans=(ans+(f(r)-f(l-1))%mod*(sum[n/l]-1)+mod)%mod;
	}
	return ans;
}
int main(){
	LL n;scanf("%lld",&n);
	init(n);
	printf("%lld",block(n));
	return 0;
}