数论基础
说在前面的话
我认为莫反之类的数学并没有想象中的那么难,其实就是掌握几个关键性质,记记结论,然后大部分的题目基本上都是套路题,难的是推式子,而不是莫反本身。
下面的很多证明是作者自己证的,有错误的地方还请提出,以供修改。
狄利克雷卷积
定义
对于两个积性函数 \(f(x)\) 和 \(g(x)\) ,它们的狄利克雷卷积结果为:
简记为:$$h=f \times g$$
结论
两个积性函数的狄利克雷卷积也是积性函数。
证明:假设 \(\gcd(a,b)=1\),有:
由于 \(\gcd(a,b)=1\),因此对于所有的 \(d_1\) 和 \(d_2\) 都是互质的,即:
因此:$$f(d)=f(d_1)f(d_2),g(\frac{ab}{d})=g(\frac{a}{d_1})g(\frac{b}{d_2})$$
上式等于:$$h(a)h(b)=\sum_{d \mid ab}f(d)g(\frac{ab}{d})=h(ab)$$
因此,\(h(x)\) 也是一个积性函数。
莫比乌斯反演
定义
先讲讲莫比乌斯函数的定义:
\(\mu(x) =\begin{cases} 1 &n=1 \\ 0 &n含有平方因子 \\ (-1)^k &k为n的本质不同质因子个数 \end{cases}\)
我们对 \(n\) 进行质因数分解,
\(n= \prod_{i=1}^k p_i^{c_i}\),其中 \(p_i\) 是质因子,而 \(c_i \ge 1\).
-
\(n=1\),\(\mu(n)=1\),显然这是积性函数都有的性质。
-
\(n \ne 1\),
- 若存在 \(i\in [1,k]\),使得 \(c_i>1\),那么 \(\mu(n)=0\)。平方因子就是次数为 \(2\) 的质因子。若 \(c_i=2\) , 没什么好说的。若 \(c_i>2\) ,可以化成 \(p_i \times p_i^2\) 的形式。
- 若不存在 \(i\in [1,k]\),使得 \(c_i>1\),那么 \(\mu(n)=(-1)^k\)。
线性筛求莫比乌斯函数
根据定义,若 \(n\) 为质数,\(\mu(n)\) 显然等于 \(-1\)。
若 \(n\) 不是质数,设 \(n\) 会被 \(i\) 和 \(p_j\) 筛掉。
分类讨论 \(i\) 和 \(p_j\) 之间的关系。
-
若 \(p_j \mid i\),\(n=\prod_{i=1}^k p_i^{c_i} ... p_j^{c_j+1}\),显然 \(c_j>1\) ,因此 \(\mu(n)=0\)
-
若 \(p_j \nmid i\),那么根据积性函数的性质:若 \(\gcd(a,b)=1\),有 \(f(ab)=f(a)f(b)\),那么 \(\mu(n)=\mu(i*p_j)=\mu(i)*\mu(p_j)\),而 \(\mu(p_j)=-1\),因此 \(\mu(n)=-\mu(i)\)。
void init(){
memset(v,0,sizeof(v));pr=0;
mu[1]=1;
for(int i=2;i<=N;i++){
if(!v[i]){
prime[++pr]=i;
mu[i]=-1;
}
for(int j=1;j<=pr&&i*prime[j]<=N;j++){
v[i*prime[j]]=1;
if(i%prime[j]==0){
mu[i*prime[j]]=0;
break;
}
mu[i*prime[j]]=-mu[i];
}
}
}
性质
莫比乌斯函数有下面性质:$$\sum_{d \mid n} \mu(d)=[n=1]= \varepsilon (n)$$
即:$$\mu \times 1=\varepsilon$$
其中,\([n]\) 表示命题 \(n\) 为真,就返回 \(1\),否则返回 \(0\)。
证明:
-
若 \(n=1\) ,显然 \(\sum_{d \mid 1} \mu(d)=[n=1]=1= \varepsilon (1)\)
-
若 \(n \ne 1\) ,考虑将 \(n\) 进行质因数分解,即:$$n= \prod_{i=1}^k p_i^{c_i}$$对于每个质因子都有 \(0 \sim c_i\) 共 \(c_i+1\) 种情况,我们画个图看看。
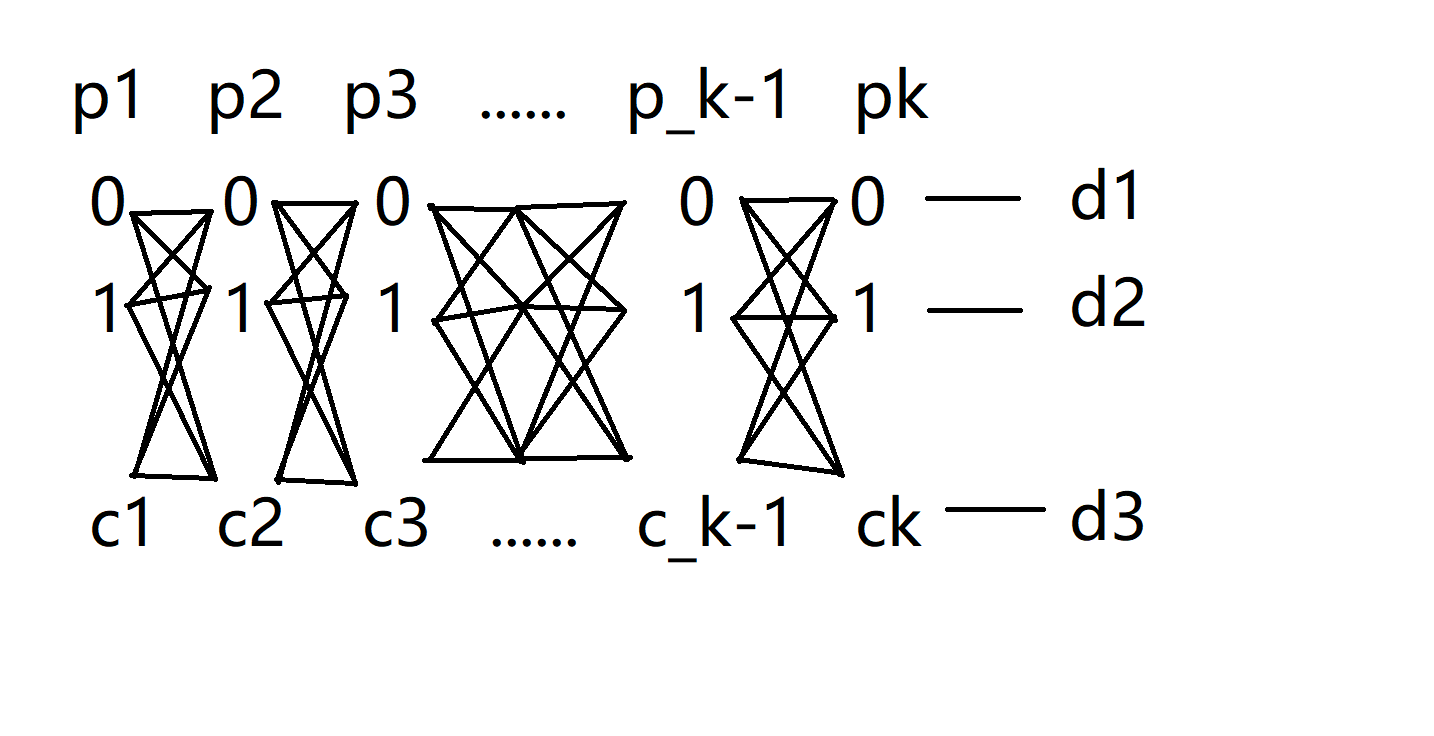
显然我们枚举的 \(d\) 都是由 \(n\) 的质因子构成的,而我们知道,当某个质因子的次数 \(c_i>1\) 时,此时 \(\mu(d)=0\),因此下面的部分我们可以不用考虑。
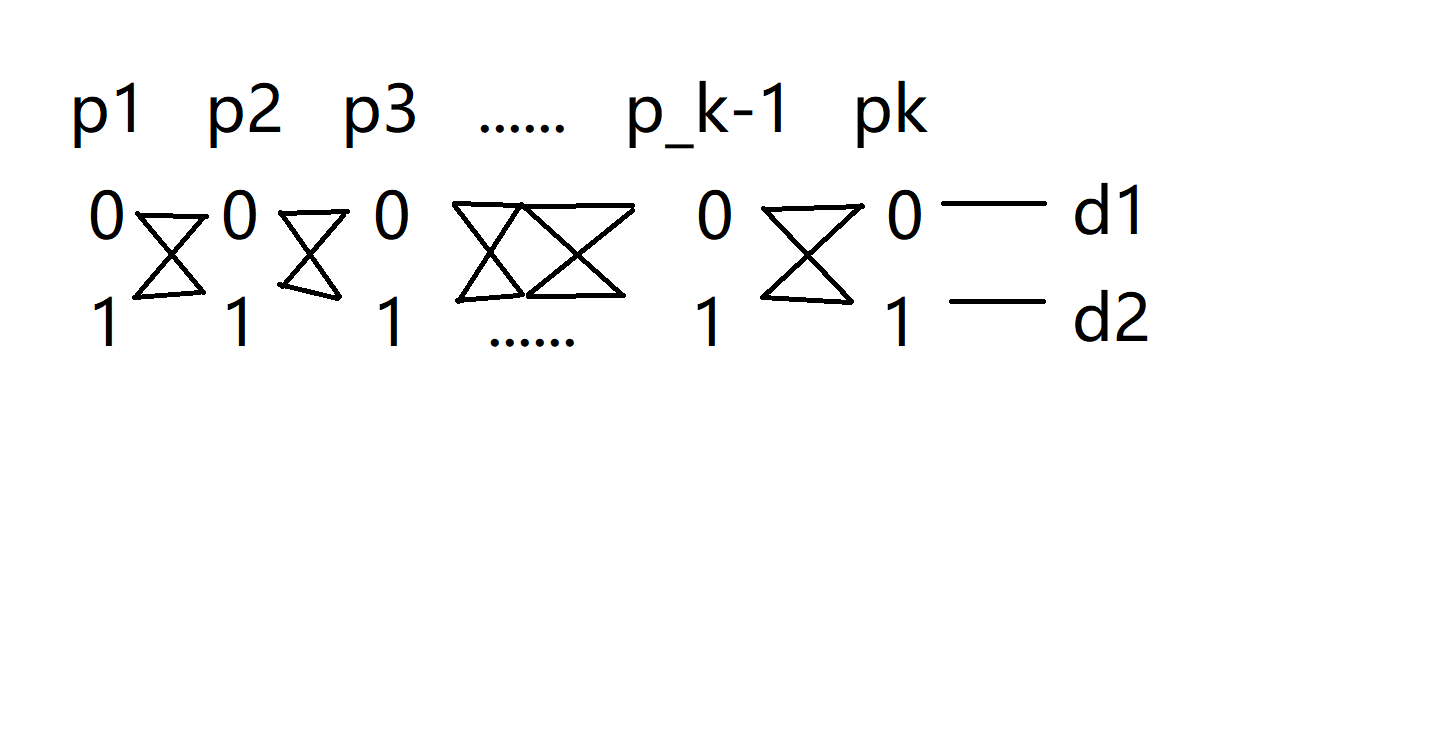
那么每个质因子就有两种情况,选或不选。
在 \(k\) 个质因子中选 \(i\) 个质因子出来共有 \(C_k^i\) 种情况,而每种情况对应的 \(\mu(d)=(-1)^k\)。
因此 $$\sum_{d \mid n}\mu(d)=\sum_{i=0}^k \binom{k}{i} (-1)^i$$
而根据二项式定理: $$(a+b)^n= \sum_{i=0}^n \binom{n}{i} a^i b^{n-i}$$
上式等于:$$(-1+1)^k=0$$
因此当 \(n \ne 1\) 时,\(\sum_{d \mid n}\mu(d)=0\)
所以 \(\sum_{d \mid n}\mu(d)=[n=1]\),根据 \(\varepsilon(n)=[n=1]\),
因此:$$\sum_{d \mid n}\mu(d)=[n=1]=\varepsilon(n)$$
结论
结论1
根据性质推出:$$[\gcd(i,j)=1]=\sum_{d \mid \gcd(i,j)} \mu(d)$$
证明:\([\gcd(i,j)=1]=\varepsilon(\gcd(i,j))=\sum_{d \mid \gcd(i,j)} \mu(d)\)
结论2
还有一个结论:$$\varphi \times 1=id$$
证明:略。
结论3
由 \(\varphi \times 1=id\),可以得出: $$\varphi(n)=\sum_{d \mid n}d \mu(\frac{n}{d})$$
证明:式子两边同时乘 \(\mu\),因此 $$\varphi \times 1 \times \mu=id \times \mu$$
根据狄利克雷卷积,可知:$$\sum_{d \mid n} \varphi(d) \varepsilon(\frac{n}{d})=\sum_{d \mid n} id(d) \mu(\frac{n}{d})$$
莫比乌斯变换与反演
定义
设 \(f(n)g(n)\) 为两个数论函数。
如果有 \(f(n)=\sum_{d \mid n}g(d)\),那么有 \(g(n)=\sum_{d \mid n}\mu(d)f(\frac{n}{d})\)。
其中,\(f(n)\) 称为 \(g(n)\) 的莫比乌斯变换,\(g(n)\) 称为 \(f(n)\) 的莫比乌斯反演。
证明
交换求和顺序,有:
例题
ZAP-Queries
令 \(i=\frac{i}{k},j=\frac{j}{k}\),
根据莫反性质 \(\sum_{d \mid n}\mu(d)=\varepsilon(n)\),可以得出:
由于交换求和顺序前枚举的是 \(i\),而 \(d\) 是 \(i\) 的约数,
因此交换求和顺序后枚举 \(d\),\(i\) 就是 \(d\) 的倍数。
显然 \(1 \sim \lfloor \frac{n}{k} \rfloor\) 里 \(d\) 的倍数共有 \(\lfloor \frac{n}{kd} \rfloor\) 个。
或者我们换种理解方式,变换前枚举的是 \(i\),变换后要枚举 \(d\),因此还要枚举 \(\frac{i}{d}\),而原来 \(i\) 的范围是 \(1 \sim \lfloor \frac{n}{k} \rfloor\),因此 \(\frac{i}{d}\) 的范围就是 \(1 \sim \lfloor \frac{n}{kd} \rfloor\)
式子也同样是:
这个式子可以用数论分块解决。
时间复杂度:\(O(T \sqrt n)\)
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=5e4;
int v[N+5],prime[N+5],pr;
int mu[N+5];LL sum[N+5];
void init(){
memset(v,0,sizeof(v));pr=0;
mu[1]=1;
for(int i=2;i<=N;i++){
if(!v[i]){
prime[++pr]=i;
mu[i]=-1;
}
for(int j=1;j<=pr&&i*prime[j]<=N;j++){
v[i*prime[j]]=1;
if(i%prime[j]==0){
mu[i*prime[j]]=0;
break;
}
mu[i*prime[j]]=-mu[i];
}
}
for(int i=1;i<=50000;i++)
sum[i]=sum[i-1]+mu[i];
}
LL block(LL n,LL m){
LL ans=0;
for(LL l=1,r=0;l<=min(n,m);l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(sum[r]-sum[l-1])*(n/l)*(m/l);
}
return ans;
}
int main(){
init();
int t;scanf("%d",&t);
while(t--){
LL n,m,k;
scanf("%lld%lld%lld",&n,&m,&k);
printf("%lld\n",block(n/k,m/k));
}
return 0;
}
Problem b
首先,如果式子是:$$\sum_{i=1}^n \sum_{j=1}^m [\gcd(i,j)=k]$$
那我们可以轻易地解决这个问题,但是 \(i,j\) 并不是从 \(1\) 开始枚举的。
因此考虑容斥。
记 $$solve(n,m)=\sum_{i=1}^n \sum_{j=1}^m [\gcd(i,j)=k]$$
那么答案就是:$$solve(n,m)-solve(x-1,m)-solve(n,y-1)+solve(x-1,y-1)$$
具体的原理就像二维前缀和一样。

橙色:\(solve(x-1,y-1)\)
橙加黄:\(solve(n,y-1)\)
橙加绿:\(solve(x-1,m)\)
橙加黄加绿加红:\(solve(n,m)\)
建议读者自己模拟一下,以加深印象。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=5e4;
int v[N+5],prime[N+5],pr;
int mu[N+5],sum[N+5];
void init(){
memset(v,0,sizeof(v));pr=0;
mu[1]=1;
for(int i=2;i<=N;i++){
if(!v[i]){
prime[++pr]=i;
mu[i]=-1;
}
for(int j=1;j<=pr&&i*prime[j]<=N;j++){
v[i*prime[j]]=1;
if(i%prime[j]==0){
mu[i*prime[j]]=0;
break;
}
mu[i*prime[j]]=-mu[i];
}
}
for(int i=1;i<=N;i++)
sum[i]=sum[i-1]+mu[i];
}
int block(int n,int m){
int ans=0;
for(int l=1,r=0;l<=min(n,m);l=r+1){
r=min(n/(n/l),m/(m/l));
ans=ans+(sum[r]-sum[l-1])*(n/l)*(m/l);
}
return ans;
}
int main(){
init();
int t;scanf("%d",&t);
while(t--){
int n,m,a,b,k;scanf("%d%d%d%d%d",&a,&n,&b,&m,&k);
printf("%d\n",block(n/k,m/k)-block((a-1)/k,m/k)-block(n/k,(b-1)/k)+block((a-1)/k,(b-1)/k));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号