【Algorithm】02_排序

1 冒泡排序

• 原理：在冒泡排序的一趟中，每次比较两个元素，根据某种原则交换元素（大于交换或小于交换），让最大的元素或最小的元素“冒泡”到列表的最右侧，第i趟的遍历范围为[0, n-1-i]，共进行n-1趟。
• 时间复杂度：O (N²)

1	def BubbleSort(lis): #降序排列
2	    for i in range(len(lis) - 1): #一趟
3	        for j in range(len(lis) - 1 - i):
4	            if lis[j] < lis[j + 1]:
5	                lis[j], lis[j + 1] = lis[j + 1], lis[j]

• 优化：如果一趟中没有任何元素交换，表明排序已经完成。

1	def BubbleSort(lis): #降序排列
2	    for i in range(len(lis) - 1): #一趟
3	        exchange = False
4	        for j in range(len(lis) - 1 - i):
5	            if lis[j] < lis[j + 1]:
6	                lis[j], lis[j + 1] = lis[j + 1], lis[j]
7	                exchange = True
8	        if not exchange: 
9	            return

　　

2 选择排序

• 原理：遍历列表，每次选择最大或最小的元素，和无序区的首个元素进行位置交换。第i趟遍历的区间为[i, n-1]，一共进行n-1趟。
•  时间复杂度：O (N²)

1	def SelectSort(lis): #降序排列
2	    for i in range(len(lis) - 1): #一趟
3	        maxIdx = i
4	        for j in range(i+1, len(lis)):
5	            if lis[maxIdx] < lis[j]:
6	                maxIdx = j
7	        if i != maxIdx:
8	            lis[i], lis[maxIdx] = lis[maxIdx], lis[i]

　　

3 插入排序

• 原理：在一趟中，选择无序区的首个元素，遍历有序区，将元素插入合适的位置，一共进行n-1趟。
• 时间复杂度：O (N²)

1	def InsertSort(lis): #降序排列
2	    for i in range(1, len(lis)): #一趟
3	        cur = lis[i]
4	        j = i - 1
5	        while lis[j] < cur and j >= 0:
6	            lis[j + 1] = lis[j]
7	            j -= 1
8	        lis[j + 1] = cur

　　

4 快速排序

• 原理：将列表第一个元素归位，形成左边元素小于（大于）它、右边元素大于（小于）它的局面，然后递归处理左侧元素列表和右侧元素列表，当要被处理的列表只有1个元素时，递归结束。递归处理方式是：将第一个元素暂存起来，从右侧开始寻找比第一个元素小（大）的数，放入左侧空位，再从左侧开始寻找比第一个元素大（小）的数，放入右侧空位，重复步骤直到左侧指针和右侧指针相遇，将第一个元素归位。
• 时间复杂度：O (NlogN)，N是每次分割所用的时间，logN是分割次数。

1	def Partition(lis, start, end):
2	    tmp = lis[start]
3	    while start < end:
4	        # 从右侧查找
5	        while lis[end] <= tmp and start < end: # 注意这里的等号，没有会进入死循环
6	            end -= 1
7	        lis[start] = lis[end]
8	        # 从左侧查找
9	        while lis[start] >= tmp and start < end:
10	            start += 1
11	        lis[end] = lis[start]
12	    lis[start] = tmp
13	    return start
14	                
15	def _FastSort(lis, start, end): #降序排列
16	    if start < end: #递归终止条件
17	        mid = Partition(lis, start, end)
18	        _FastSort(lis, start, mid - 1)
19	        _FastSort(lis, mid + 1, end)
20	
21	def FastSort(lis):
22	    _FastSort(lis, 0, len(lis) - 1)

• 注意点：

①    第5行的循环条件要有等号，否则会进入死循环。

②    第16行的判断符是if而不是while，否则会进入死循环。

• 问题：

①    注意递归最大深度。

②    最坏情况：初始列表是有序的，且与目标顺序正好相反，时间复杂度会变成O (N²)。一个解决方法是，随机选择要归位的元素，这样可以保证初始列表的顺序无效。

 

5 堆排序

• 堆：一种特殊的完全二叉树。
  • 　　大根堆：一棵完全二叉树，它的任一节点都比其孩子节点大。
  • 　　小根堆：一棵完全二叉树，它的任一节点都比其孩子节点小。

 

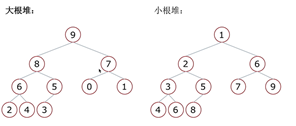
• • 　　向下调整性质：当节点的左右子树都是堆，但自身不是堆时，可以通过一次向下调整将其调整为堆。

  

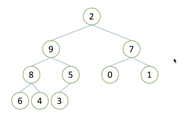
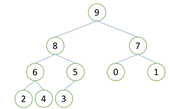
• 原理：构建一个大根堆（降序排序）或小根堆（升序排序），堆顶的数就是要取的数，每次取完后将最后一个叶子节点移到堆顶，通过一次向下调整让堆变得有序（简而言之，就是“取、移、调”三步骤的循环）。构建堆的方法是自下而上的向下调整。
• 时间复杂度：O (NlogN)

1	def Sift(lis, start, end): # 向下调整函数，大根堆
2	    tmp = lis[start]
3	    idx_father = start
4	    idx_child = 2 * idx_father + 1
5	    idx_child = idx_child + 1 if idx_child < end and lis[idx_child] < lis[idx_child + 1] else idx_child
6	    while idx_child <= end and lis[idx_child] > tmp:
7	        lis[idx_father] = lis[idx_child]
8	        idx_father = idx_child
9	        idx_child = 2 * idx_father + 1
10	        idx_child = idx_child + 1 if idx_child < end and lis[idx_child] < lis[idx_child + 1] else idx_child
11	    lis[idx_father] = tmp
12	
13	def HeapSort(lis): # 升序排序，大根堆
14	    num = len(lis)
15	    # 建堆
16	    for i in range((num-2)//2, -1, -1):
17	        Sift(lis, i, num - 1)
18	    # 取移调循环
19	    for i in range(num - 1):
20	        lis[0], lis[num - 1 - i] = lis[num - 1 - i], lis[0]
21	        Sift(lis, 0, num - 2 - i)

• 注意点：

①    如第5、10行，在需要使用idx_child+1时，必须先判断idx_child+1是否越界。

 

6 归并排序

• 原理：将一个列表递归地半分，直到列表只有1个元素（可视为有序列表）；再将半分后的列表递归地合并起来。
• 时间复杂度：O (NlogN)

1	# 合并两个有序列表，升序排序
2	# start是第一个列表的起始位置
3	# mid是第一个列表的终止位置
4	# end是第二个列表的终止位置
5	def Merge(lis, start, mid, end):
6	    res = []
7	    i = start
8	    j = mid + 1
9	    while i <= mid and j <= end:
10	        if lis[i] < lis[j]:
11	            res.append(lis[i])
12	            i += 1
13	        else:
14	            res.append(lis[j])
15	            j += 1
16	    while i <= mid:
17	        res.append(lis[i])
18	        i += 1
19	    while j <= end:
20	        res.append(lis[j])
21	        j += 1
22	    lis[start : end + 1] = res
23	
24	def _MergeSort(lis, start, end):
25	    if start < end:
26	        mid = (start + end) // 2
27	        _MergeSort(lis, start, mid)
28	        _MergeSort(lis, mid + 1, end)
29	        Merge(lis, start, mid, end)
30	
31	def MergeSort(lis):
32	    _MergeSort(lis, 0, len(lis) - 1)

　　

7 希尔排序

• 原理：由插入排序引申而来，是一种分组插入排序，以间隔为gap的若干元素为一组，进行若干次排序，gap逐渐减小至1.
• 时间复杂度：依赖于gap，不好说。

1	def InsertSortGap(lis, gap): # 升序排列
2	    for i in range(gap, len(lis)):
3	        tmp = lis[i]
4	        j = i - gap
5	        while j >= 0 and lis[j] > tmp:
6	            lis[j + gap] = lis[j] 
7	            j -= gap
8	        lis[j + gap] = tmp
9	
10	def ShellSort(lis):
11	    gap = len(lis) // 2
12	    while gap >= 1:
13	        InsertSortGap(lis, gap)
14	        gap //= 2

 

8 基数排序

• 原理：准备0-9号10个桶，先将元素按个位数分入桶中（桶就像一个队列），分好后依次将元素从桶中取出，再将元素按十位数分入桶中，分好后依次将元素从桶中取出，再将元素按百位数分入桶中…重复上述步骤，重复最大值的位数次。
• 时间复杂度：O (kN)，k代表最大值的位数

1	def RadixSort(lis):
2	    max_element = max(lis)
3	    iter_num = int(math.log(max_element, 10)) + 1
4	    for i in range(iter_num):
5	        buckets = [[] for _ in range(10)]
6	        for element in lis:
7	            digit = element // 10 ** i % 10
8	            buckets[digit].append(element)
9	        lis.clear()
10	        for buc in buckets:
11	            lis.extend(buc)