计算机视觉中由基本矩阵F或者本质矩阵E计算摄像机投影矩阵时，经常提到“相差一个尺度因子”的含义
在通过二维像素坐标恢复三维坐标的过程中，经常出现这个齐次坐标系、尺度不变性的概念。这篇博客讲的比较好。
一、关于齐次坐标系的直观感受
在我们的世界里，两平行线是永远不会相交的，但是在投影空间里，两条平行线在无穷远处是相交的，如这个铁轨一样：
在数学里，我们通过齐次变换来表示这种问题，齐次变换就是将一个原本是n维的向量用一个n+1维向量来表示。
为了制作二维齐次坐标，我们只需在现有坐标中添加一个额外的变量 w。 因此，笛卡尔坐标中的点 (X, Y) 变为齐次坐标中的 (x, y, w)，这两个坐标描述的是同一点。 为了将齐次坐标 (x, y, w) 转换为笛卡尔坐标，我们只需将 x 和 y 除以 w：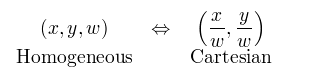
例如，笛卡尔坐标系下（1，2）的齐次坐标可以表示为（1，2，1），如果点（1，2）移动到无限远处，在笛卡尔坐标下它变为(∞,∞)，然后它的齐次坐标表示为（1，2，0），因为(1/0, 2/0) = (∞,∞)，我们可以不用”∞”来表示一个无穷远处的点了。
二、关于其次坐标的尺度不变性
转化齐次坐标到笛卡尔坐标的过程中，我们可以发现：
齐次坐标系点 (1, 2, 3), (2, 4, 6) 和 (4, 8, 12) 对代表欧几里得空间（或笛卡尔空间）中的同一点(1/3, 2/3)。
三、相差一个尺度因子的含义
在SLAM或者其它视觉感知的问题中常常会出现这样子的齐次坐标系构成的等式，如：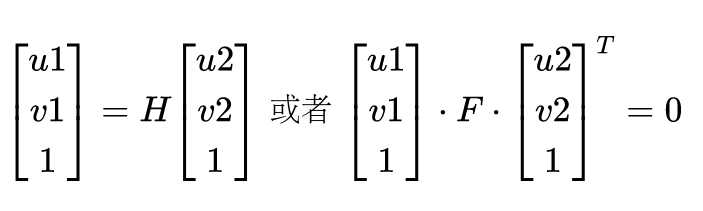
其中H或E为一个三乘以三的矩阵，应该有9个变量。这个时候经常会看到一句话，说由于尺度等价性，H或E只有8个自由度，这是什么意思呢？
上式的(u, v, 1)为齐次坐标，其乘以任意常数意义不变（等式依然成立），对应的H或E也应该满足这一点。说得更加具体一点，H或E可以有无数解，但这些解都是倍数关系，例如H或E的解可以为：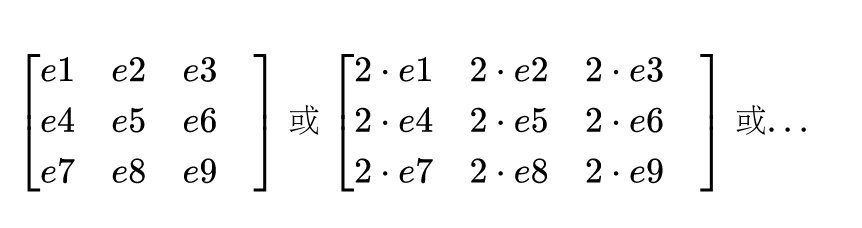
这么多解肯定不是我们想要的，所以我们进行一个归一化，规定H或E矩阵的最后一个元素的值为1，这样我们的解就唯一了。
至于为什么叫做“尺度等价性”，因为我们将这个值设置为1对应到真实世界中的长度可能是5cm,也可能是40m，这就需要额外的深度信息介入进行确定，这个以t的长度作为单位的尺度世界只和真实世界之间相差一个“尺度因子”。
所以我们在计算的时候说，由于“尺度不变性”，该三乘以三的矩阵有八个自由度（也就是有8个元素是未知量），还有一个元素作为尺度被设置为1（这个1乘以一个“尺度因子”就是实际的尺度）。
