数论(3) | 中国剩余定理与拓展中国剩余定理

1 中国剩余定理crt(洛谷P3868)

已知同余方程组:

 

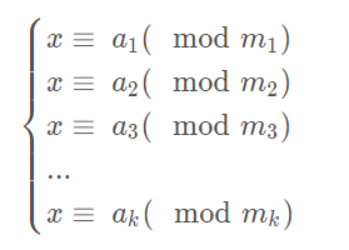
 求x的最小非负整数解。

推荐一篇超棒的博客 -> https://www.cnblogs.com/MashiroSky/p/5918158.html

大多数题解都是上来就一堆公式，看的很累。这个大佬的博客上来先演示了一遍中国剩余定理的运算过程，再上公式就清楚了：

在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之剩二（除以7余2），问物几何？”

解决这个问题需要三步：

1.找到三个数：从3和5的公倍数中找出被7除余1的最小数15，从3和7的公倍数中找出被5除余1 的最小数21，最后从5和7的公倍数中找出除3余1的最小数70。

2.用15乘以2（七七数之剩二），用21乘以3（五五数之剩三），同理，用70乘以2（三三数之剩二），然后相加15*2+21*3+70*2=233。

3.用233除以3，5，7三个数的最小公倍数105，得到余数23，即233%105=23。这个余数23就是符合条件的最小数。

这是理解crt的关键。其实读到这里再自己思考一下就可以理解其原理了。还有不理解的可以参考博客原文，这里也就不再复制粘贴了。下面直接给出公式：

其中，

 前提：m_i必须保证互质！（比如现在我们要找一个模6余2，模9余5的数字，根据中国剩余定理，我们要先在9的倍数中找到一个模6余1的数，这显然是不存在的。但模6余2，模9余5的数字还是有的，比如15）

那如果不互质怎么办呢？一会儿会讲excrt。先把crt的代码给出来。

#include <bits/stdc++.h>//中国剩余定理
using namespace std;
typedef long long LL;
LL mul(LL x,LL y,LL p){
    LL ans=0;
    while (y){
        if (y&1) ans=(ans+x)%p;
        y>>=1;
        x=(x*2)%p;
    }
    return ans;
}
LL exgcd(LL a,LL b,LL &x,LL &y){
    if (b==0){
        x=1;y=0;
        return a;
    }
    LL r=exgcd(b,a%b,x,y);
    LL t=x;
    x=y;
    y=t-(a/b)*y;
    return r;
}
int main(){
    int n;
    long long a[11],b[11];
    scanf("%d",&n);
    LL M=1,ans=0,x,y;
    for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
    for (int i=1;i<=n;i++) scanf("%lld",&b[i]),M*=b[i];
    for (int i=1;i<=n;i++) a[i]=(a[i]%b[i]+b[i])%b[i];
    for (int i=1;i<=n;i++){
        LL t=M/b[i];
        exgcd(t,b[i],x,y);
        x=(x%b[i]+b[i])%b[i];
        ans=(ans+mul(mul(t,x,M),a[i],M))%M;
    }
    printf("%lld",ans);
    return 0;
}

2 中国剩余定理excrt(洛谷P4777)

当m_i不保证互质的时候，我们不能直接使用中国剩余定理，而是首先要进行两两合并。

比如现在m₁，m₂不互质，我们要合并下面两个式子： 

 联立，得：

因为a>0,m>0,我们要找到一个x最小的正整数特解x’，就要求出x₁(或者x₂)的最小正整数解，exgcd一下就可以了。最终式子可以合并为

（接上面的例子，我们要找一个模6余2，模9余5的数字，变换式子得6x₁+9x₂=1，exgcd求得x特解14。又因6和9的公倍数是18，两个式子可以合并为x≡14（mod 18），接下来找x只需要在14+18k里面找就行了。）

贴代码！

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL exgcd(LL a,LL b,LL &x,LL &y){
    if (b==0){
        x=1;y=0;
        return a;
    } 
    LL r=exgcd(b,a%b,x,y);
    LL t=x;
    x=y;
    y=t-(a/b)*y;
    return r;
}
LL mul(LL a,LL b,LL m){
    LL x=b,y=0;
    while (a){
        if (a&1) y=(y+x)%m;
        x=(x+x)%m;
        a>>=1;
    }
    return y;
}
int main(){
    LL a[100001],b[100001],n,sum=0;
    scanf("%lld",&n); 
    for (int i=1;i<=n;i++){
        scanf("%lld%lld",&a[i],&b[i]);
    }
    LL M=a[1],ans=b[1];
    for (int i=2;i<=n;i++){//已知k-1个式子的特解ans和最小公倍数M，现要加上第k个式子。ans+t*M=b[j] (mod a[i]) 
        LL x,y,c,g,t;
        c=(b[i]-ans%a[i]+a[i])%a[i];//防止b[i]-ans为负数 
        g=exgcd(a[i],M,x,y);//拓展欧几里得a[i]*x+M*y=c 
        if (c%g) {
            cout<<"Impossible";
            return 0;
        }
        t=a[i]/g;
        y=mul(c/g,y,t);//放大 
        y=(y%t+t)%t;//求最小正整数解 
        ans=ans+mul(y,M,M*(a[i]/g));
        M=M*(a[i]/g);
        ans=(ans%M+M)%M;//更新ans与M 
    }
    cout<<ans;
    return 0;
}