11.22 game

坠机，rk 10。

\(t2\) 挂成 \(28\)pts。t3 大半人 ac 我想了 \(40+min\) 没有任何思路。

\(t2\) \(10\) 个大样例全过也能挂成这样，说明拍子的重要性；同时说明规划代码环节必须根据自己的思路想清楚细节在下手。

\(t3\) 的思考大多无效！如果大脑思考遇到瓶颈，可以尝试在纸上整理已知的信息（转化成图片/数学语言）（但是不能像 CSP-S \(t1\) 通过在纸上随便写东西假装自己在思考）。

t1

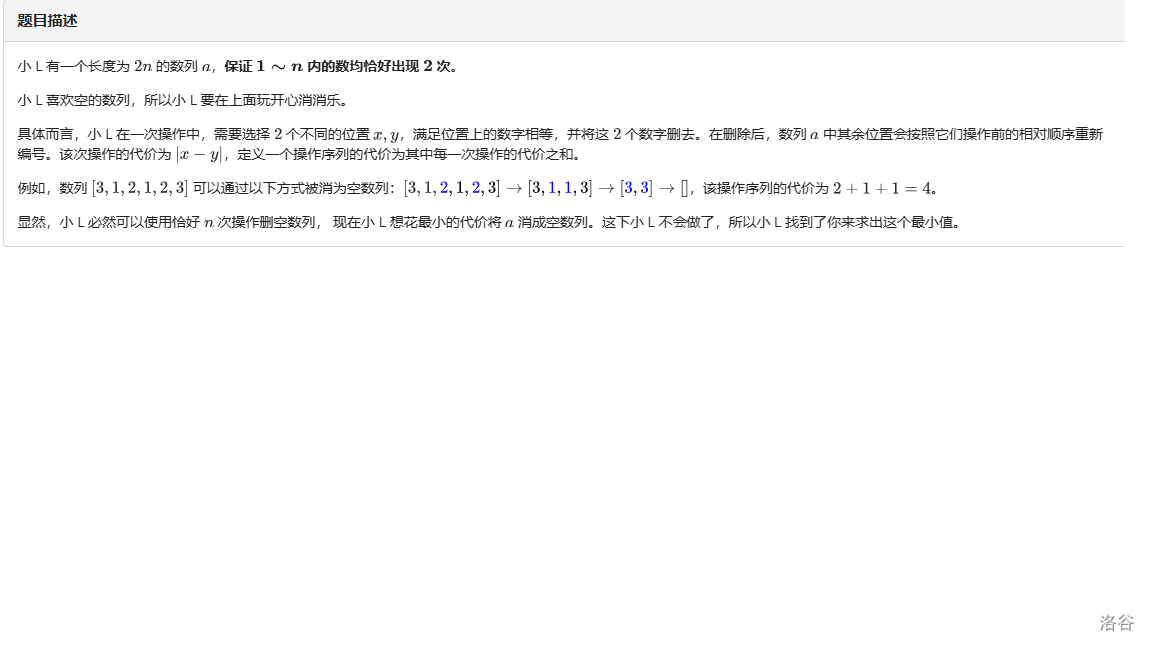
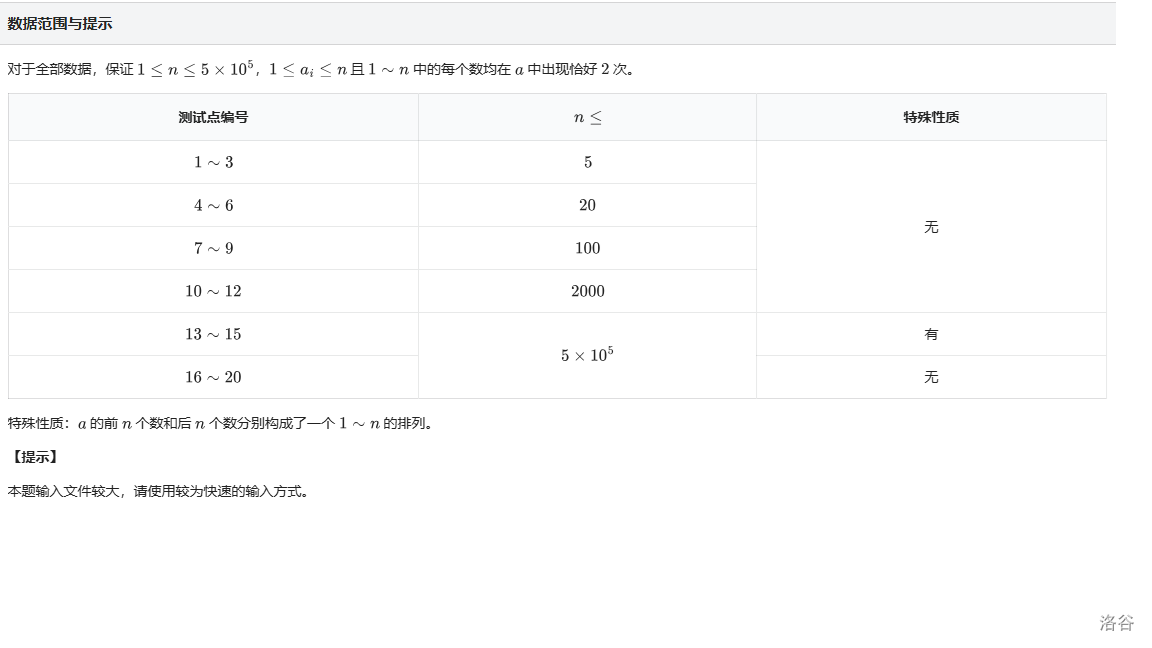
简单题。

有点类似 这题，可以发现操作顺序和区间的位置关系有关。

注意到非包含的区间（包括相离和相交两种情况）都不关心操作顺序，只有包含的区间应当先操作小区间。

所以按区间长度从小到大操作，删除一个数和查询位置可以用 \(01\) 树状数组维护。

t2

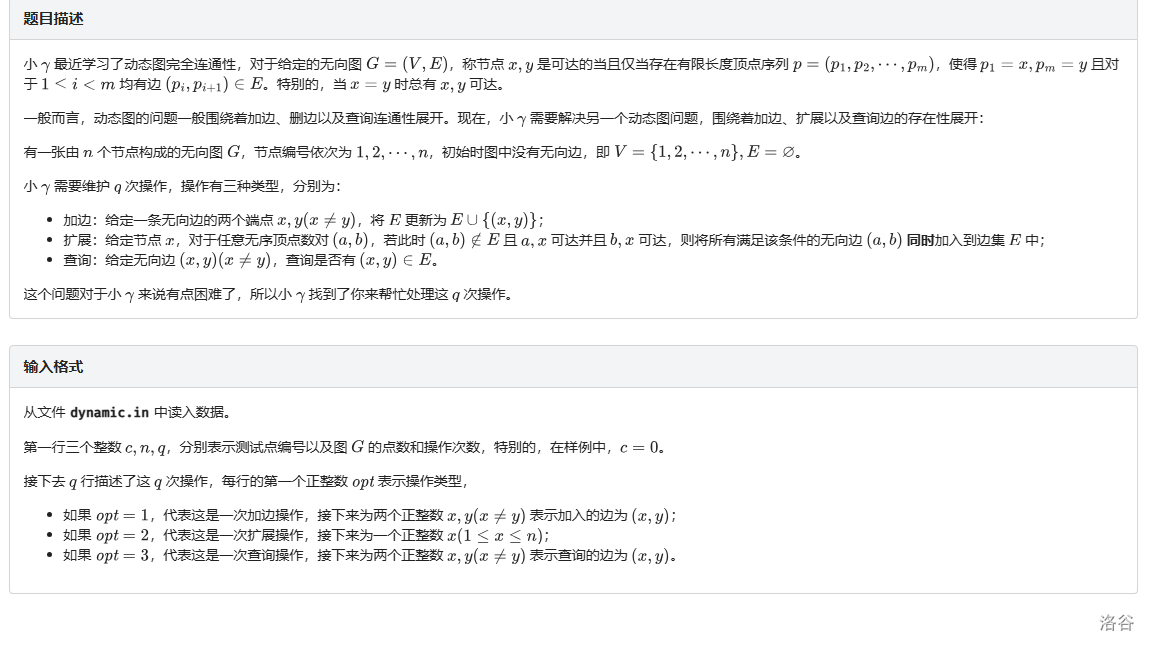
操作一是好做的。

操作二相当于将 \(x\) 所在连通块变成完全图，所以可以用一个并查集记录每个点所属完全图编号，然后每次操作就将 \(x\) 所在联通块的所有点缩成一个新点。

这样操作一的连边相当于在完全图之间连边，但是记录的边仍然是原边。

两个点有连边，等价于其连通块编号相等或者有被直接连边。

t3

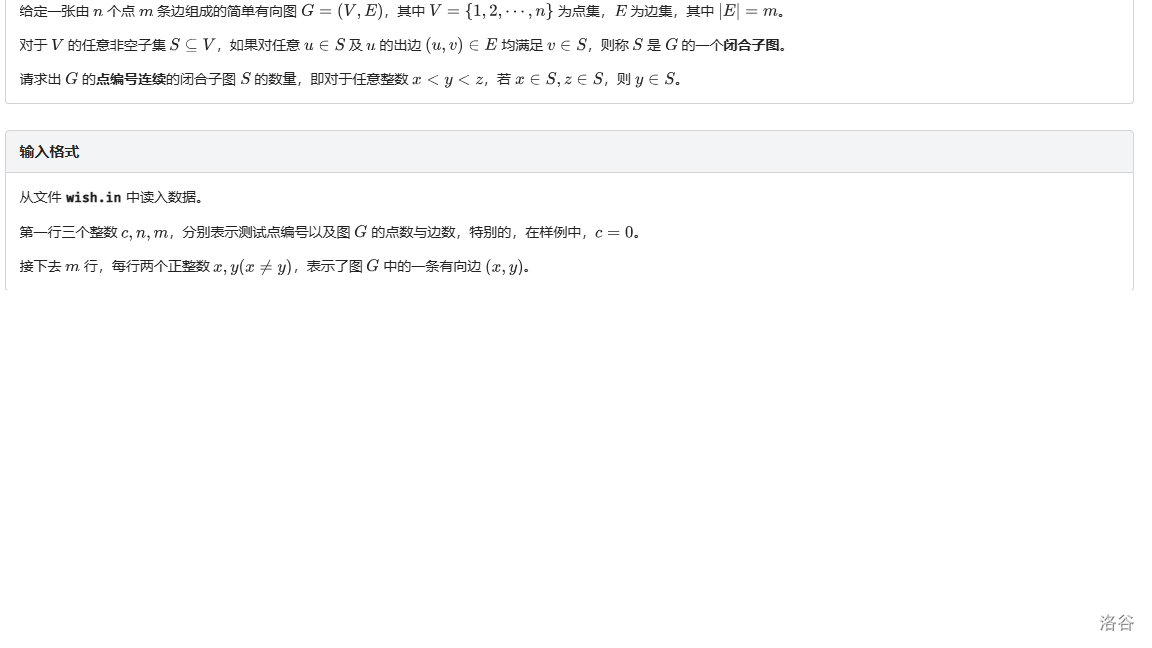
枚举区间，判断是否能由若干闭合子图组成。

区间 \([l,r]\) 合法，等价于 \(\bigcup_{i=l}^{r} S(x) = \{x \in Z|l \leq x \leq r\}\)。

\(O(n^2)\) 是给每个点附随机权值，用亦或哈希判断集合相等；枚举左端点，从小到大依次将 \(S(r)\) 加入并且判断是否合法。加入一个集合相当于直接 dfs，加上记忆化可以做到单个左端点的操作次数是 \(O(n)\)。

注意到答案总数是 \(O(n^2)\)，所以基于答案的做法肯定不行。

套路地，枚举左端点，考虑能否快速求出合法的右端点。

需要 \([l,r]\) 合法的进一步性质。

容易发现 \(O(n^2)\) 的做法很唐（赛时止步于此）。因为 \(x \subseteq S(x)\)，所以 \(\{x \in \Z|l \leq x \leq r\} \subseteq \bigcup_{x=l}^{r} S(x)\)。因此两个集合相等等价于后者包含于前者，而这要求 \(\forall x \in \bigcup_{x=l}^{r} S(x),l \leq x \leq r\)。

不妨记 \(\bigcup_{x=l}^{r}S(x)\) 的元素最小值为 \(mi\)，最大值为 \(mx\)，上述要求等价于 \(mi \geq l,mx \leq r\)。

\(mi_x,mx_x\) 是好求的，可以缩点+tuopu排序+dp。

所以 \([l,r]\) 合法等价于 \(\min_{i \in [l,r]}\{mi_i\} \geq l,\max_{i \in [l,r]}\{mx_i\} \leq r\)。

注意到如上限制一个只与左端点有关，一个只与右端点有关；分别考虑。

记 \(s_i\) 为 \(i\) 右边第一个满足 \(mi_j \lt i\) 的 \(j\)，\(p_i\) 为 \(i\) 左边第一个满足 \(mx_j \gt i\) 的 \(j\)。对一个左端点 \(l\)，\([l,s_l-1]\) 内的点满足第一种限制；对一个右端点 \(r\)，\([p_r+1,r]\) 内的点满足第二种限制。

这种二维限制考虑扫描线，将 \(r\) 对 \(l\) 的限制扫描掉，然后 \(l\) 对 \(r\) 的限制用 ds 维护。

t4

过于困难。