11.18 num 2

num1 t1

启发意义。

对每一位考虑，注意到 \(A \xor B\) 可以视作 \(\max(A,B)-\min(A,B)\)；\(A \or B\) 可以视作 \(\max(A,B)\)；\(A+B = \max(A,B)+\min(A,B)\)。

所以合法等价于 \(y\) 是 \(x\) 的二进制子集；最后输出 \(2x-y\) 即可。

启示：

二进制意义下的基本运算可以由 \(\max,\min\) 表达。

num1 t6

启发/训练意义。

可以把每个长度为 \(k\) 的状态均相同的连续段看成一个可以任意移动和翻转的基本元；所以把两个字符串中的所有长为 \(k\) 的状态均相同的连续段删去，比较剩余部分是否相同即可。

基本元可以任意翻转是显然的。我们来证明基本元可以向两个端点方向任意移动。

考虑 \(s\) 中一个长为 \(k\) 的连续段，不妨假设其是 \(1\) 的连续段（\(0\) 连续段类似），如果其有一个端点为 \(1\)，那么你可视其移动了；剩下的端点就是 \(0\)，你可以先翻转基本元的状态，然后在将其与 \(0\) 端点合并。

num2 t3

题面

训练意义。

考虑 \(42\) 的次幂不会太多。

所以每种颜色贡献至多贡献 \(\log_{42} V\) 次加法。

对每种颜色维护其到距离其最近的 \(42\) 次幂的距离；当存在连续段的距离为负时，暴力改，每种颜色至多修改 \(\log_{42}\)。

具体地，线段树上每个节点维护 覆盖标记，距离标记最小值，加法标记。

每次加法操作后，暴力改不合法的距离标记；然后如果距离标记存在为 \(0\)，就接着加。

时间复杂度 \(O(n \log n \log_{42} V)\)。

num2 t4

启发意义。

考虑刻画颜色相同的限制。不妨对每种颜色考虑。

对于相邻的两个颜色相同的端点，其合法必然满足中间颜色均小于等于该颜色；注意到如果 \((l_1,l_2)\) 合法，\((l_2,l_3)\) 合法，那么 \((l_1,l_3)\) 合法，这种合法具有可合并性（传递性）。

对每种颜色，不妨将每个左端点向离其最近的合法的右端点连边，可以得到若干不交的链；

套路地（，对链的长度分治。

当 \(len \lt B\) 时，倍增处理链，可以做到 \(O(\dfrac{nq\log n}{B})\)；当 \(len \geq B\) 时，暴力枚举区间两个端点，根据平均长度理念 (类似 这里 \(t3\) 的分析)可以做到 \(O(nB)\)。容易平衡到 \(O(n \sqrt{n\log n})\)。

上述做法虽然看似劣，实际上跑的比正解快（）

考虑比较优美的做法。

考虑一个询问 \((L,R)\)，不妨刻画最大值的限制。

找到最大值的左右端点 \((l,r)\)，然后有 \(r-l+1\) 可以作为答案。

发现最大值起到了隔断区间的作用，即除了最大值之外的颜色不可能与 \(l,r\) 有交，所以其余答案的区间分为三类：\([L,l),(l,r),(r,R]\)，注意到中间那类肯定不优，只考虑剩余两类。

对每个点维护最大合法右端点 \(s_i\)，最小合法左端点 \(p_i\)，相当于查询 \(\max_{i \in [L,l)}\{s_i-i+1\}\) 和 \(\max_{i \in (r,R]}\{i-p_i+1\}\)。注意到上文关于无交的叙述，\(s_i\) 必然位于 \([L,l)\) 内；\(p_i\) 必然位于 \((r,R]\) 内。

用 st 表维护区间最大值，和上述两种东西的区间最大值即可。

时间复杂度 \(O(n \log n)\)。

num2 t6

启发意义。

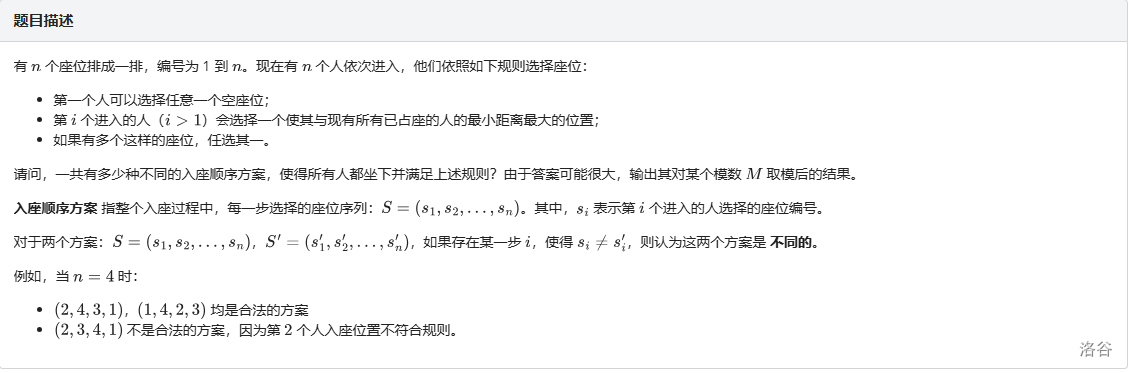
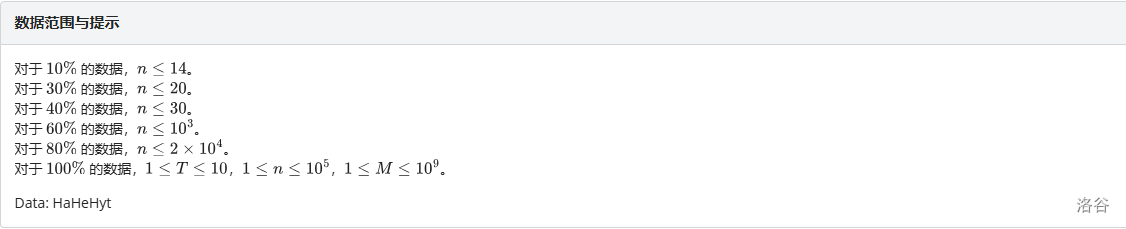
枚举第一个人的座位。

考虑限制相当于只能选某一段的中点。

不妨先只对某一段考虑，段长为奇数则中点唯一；否则中点不维一；

注意到每一段取完中点后长度必然减半，所以至多有 \(\log n\) 种不同的段长。

不妨先找到这些段长，定义 \(f_i\) 为长度为 \(i\) 的段的出现次数，然后从大往小转移，有：

\(i\) 为奇数：\(f_{\lfloor \frac{i}{2} \rfloor} \gets f_{\lfloor \frac{i}{2} \rfloor}+2f_i\)。
反之 \(f_{\frac{i}{2}} \gets f_{\frac{i}{2}}+f_i,f_{\frac{i}{2}+1} \gets f_{\frac{i}{2}+1}+f_i\)。

考虑分阶段，对当前距离为 \(k\) 的若选择统一考虑。

记这个距离被奇数段贡献了 \(a\) 次，被偶数段贡献了 \(b\) 次，则方案数为 \((a+b)!2^b\)（特殊地，距离为 \(1\) 的情况贡献为 \((a+2b)!\)）。

定义 \(g_{0/1,i}\) 表示距离为 \(i\) 被奇/偶数段的贡献次数，则有 \(g_{i\&1,\lfloor \frac{i+1}{2} \rfloor} \gets g_{i\&1,\lfloor \frac{i+1}{2} \rfloor}+f_i\)。

num2 t7

题面

启发意义。

对答案形态考虑，发现点必然被分为若干层，并且相邻层的点之间有连边。

朴素的想法是定义 \(f_{j,i}\) 表示将 \([j,i]\) 划分为一层的最小代价，每次 \(f_{j,i}\) 从 \(f_{k,j-1}\) 转移而来，判断是否合法以及代价。这是 \(O(n^3)\)。

考虑合法的限制，对于 \(f_{j,i}\)，记 \(mx_i\) 为 \([1,i]\) 内的点向后连边的点的最大值，其只能转移到 \(t \in [mx_i,n],f_{t,k}\)。

所以 \(f_{j,i}\) 的转移范围是一段后缀；并且我们不关心 \(j\) 这一维具体是什么。

考虑定义 \(f_i\) 表示将 \([1,i]\) 分成若干层，\(i\) 恰好是最后一层的末尾元素的最小代价。

（下文的 \(\gets\) 均表示可以贡献）

有 \(f_{mx_i}\gets f_i+w_{i+1,mx_i}\)，其中 \(w_{i,mx_i}\) 表示 \([i+1,mx_i]\) 中与 \([1,i]\) 没有连边的点数；注意到 \([mx_i+1,n]\) 中的每个点与 \([1,i]\) 均没有连边，所以 \(f_i\) 对 \(t \in [mx_i,n],f_t\) 的贡献是等差数列式的，可以考虑将 \(f_i\) 只贡献给 \(f_{mx_i}\)，然后加入转移 \(f_i \gets f_{i-1}+1\)。

num2 t11

启发/反思意义。

只有一个数不合法。考虑任取三个数 \(a,b,c\)，其中必然有两个数合法。

所以两两组合，钦定组合两个元素合法，求出当前 \(x\)，判断是否符合题意；总能找到一对组合符合题意。

时间复杂度 \(O(Tn)\)。

num2 t12

题面

训练意义。

假设前 \(i\) 个人都吃了。我们只关心 \([i,i+b_i-1]\) 的人的吃饭情况已经上一个用餐的人。

注意到 \(b_i\) 很小，考虑状压；同时有上一个用餐的人距离 \(i\) 至多 \(\max\{b_i\}\) 远。

定义 \(f_{i,S,j}\) 表示 \([1,i-1]\) 全吃了，第 \(i\) 个人及以后紧接着的人的用餐情况为 \(S\)， \(i-1\) 与上一个用餐的人距离之差为 \(j\) （可负）的最小代价。

如果 \(S\) 中第 \(i\) 个人吃了，将其直接转移给 \(f_{i+1,S>>1,j-1}\)；否则枚举下一个吃饭的人，顺便判断是否符合 \(b_i\) 限制。

时间复杂度 \(O(n2^{\max\{b_i\}}(\max\{b_i\})^2)\)。