3.二叉搜索树

1.二叉搜索树概述

二叉搜索树（Binary Search Tree, BST）也叫二叉排序树（Binary Sort Tree），是一种特殊的二叉树，它满足以下性质：

左子树：左子树上所有节点的值都小于根节点的值。
右子树：右子树上所有节点的值都大于根节点的值。
递归性质：左子树和右子树本身也是二叉排序树。

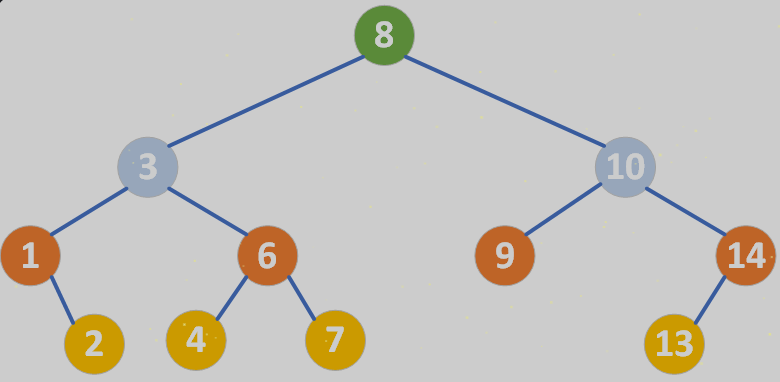
二叉搜索树的一个重要特性是，它的中序遍历（左 → 根 → 右）结果是一个有序的序列。因此，二叉搜索树常用于实现动态集合的查找、插入和删除操作。
“有序的序列” 简单说就是元素按照 “从小到大（升序）” 或 “从大到小（降序）” 的固定顺序排列的序列。

2.二叉搜索树的基本操作

2.1查找操作

平均时间复杂度为 O(log n)

从根节点开始：查找操作必须从二叉搜索树的根节点开始。
比较目标值与当前节点值
- 如果目标值 == 当前节点值，查找成功，返回该节点。
- 如果目标值 < 当前节点值，则递归查找左子树。
- 如果目标值 > 当前节点值，则递归查找右子树。
递归或迭代查找：重复上述比较过程，直到找到目标值或到达叶子节点（查找失败）。
查找结束
- 如果找到目标值，返回对应的节点。
- 如果到达叶子节点仍未找到目标值，则返回 nullptr 或表示查找失败的值。

2.2插入操作

插入操作的时间复杂度为 O(log n)，其中 n 是树中节点的数量。

从根节点开始：插入操作从二叉搜索树的根节点开始。如果树为空，则新节点成为根节点。
比较新节点的值与当前节点的值
- 如果新节点的值 < 当前节点的值，递归向左子树插入。
- 如果新节点的值 > 当前节点的值，递归向右子树插入。
- 如果新节点的值 == 当前节点的值，根据具体需求决定是否插入（BST 中通常不允许重复值）。
找到插入位置：重复上述比较过程，直到找到一个空位置（即 nullptr），然后将新节点插入到该位置。
插入完成：新节点被插入到树中，树的结构保持不变。
比如插入目标值 5

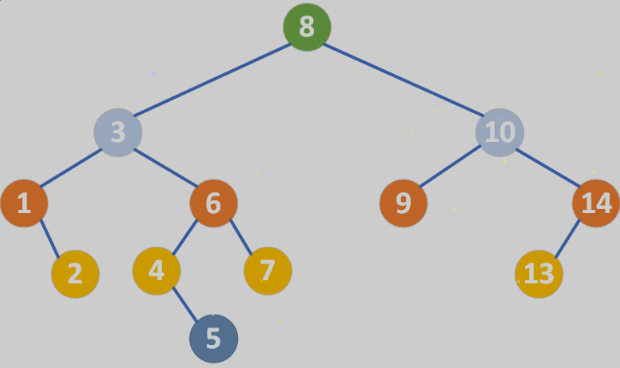
2.3删除操作

删除操作的时间复杂度为 O(log n)，其中 n 是树中节点的数量。
删除操作有以下三种情况：

删除叶子节点：如果待删除节点没有子节点，直接删除即可。
删除只有一个子节点的节点：如果待删除节点只有一个子节点，用其子节点替代被删除的节点。
删除有两个子节点的节点：
- 找到其右子树的最小值节点（或左子树的最大值节点）
- 用该节点的值替换待删除节点的值，然后删除该节点。

3.二叉搜索树的实现

3.1构造和析构

模板的编译模型：

模板的实例化需要在编译时完成，因此编译器必须能够看到模板的完整定义（包括实现）。
如果将模板的实现放到 .cpp 文件中，编译器在编译其他使用模板的源文件时无法看到模板的实现，导致无法实例化模板。
对于模板代码，编译器的处理流程如下：
- 词法分析和语法分析：与非模板代码相同。
- 模板解析：解析模板定义，但不生成代码。
- 模板实例化：在模板被使用时（如 BST），生成具体的代码。
- 代码生成：生成目标机器代码。
  为了防止编译器无法看到模板类的完整实现，导致实例化失败，我们通常会将模板的定义和实现都写在同一个 .hpp 文件中。

3.1.1构造函数

template<typename T, typename CompFunc>
BST<T, CompFunc>::BST(CompFunc comp) : m_root(nullptr), m_comp(comp) {}

功能：

初始化 BST 的根节点 m_root 为 nullptr，表示树为空。
初始化比较函数对象 m_comp，用于比较节点值。
参数：
comp：比较函数对象，默认值为 CompFunc()（即 std::less，用于升序排序）。
示例

BST<int> bst;                      // 使用默认比较函数 std::less<int>
BST<int, std::greater<int>> bst2;  // 使用 std::greater<int> 作为比较函数

3.1.2析构函数

template<typename T, typename CompFunc>
BST<T, CompFunc>::~BST()
{
    clear(m_root);
    m_root = nullptr;
}

功能：

调用 clear(m_root) 递归释放树中所有节点的内存。
将根节点 m_root 置为 nullptr，避免悬空指针。
实现细节：
clear(Node* root) 是一个辅助函数，用于递归释放树中所有节点的内存。
递归释放过程：
- 如果当前节点为空，直接返回。
- 递归释放左子树。
- 递归释放右子树。
- 释放当前节点。

3.2插入操作

3.2.1非递归实现

在二叉搜索树种插入新节点，核心逻辑如下：

树为空：
- 如果根节点 m_root 为空，直接将新节点作为根节点。
搜索插入位置：
- 使用 cur 指针从根节点开始遍历树。
- 使用 parent 指针保存 cur 的父节点地址。
- 如果当前节点的值等于待插入值，提示插入失败并返回。
- 如果当前节点的值小于待插入值，移动到右子树。
- 如果当前节点的值大于待插入值，移动到左子树。
插入新节点：
- 根据比较结果，将新节点插入到 parent 的左孩子或右孩子位置。

点击查看代码

template<typename T, typename CompFunc>
bool BST<T, CompFunc>::insertNormal(const T& value)
{
    /* 如果根节点 m_root 为空，直接将新节点作为根节点。 */
    if (m_root == nullptr)
    {
        m_root = new Node(value);
        return true;
    }
    Node* parent = nullptr;/* 用于记录当前节点的父节点 */
    Node* cur = m_root;/* 从根节点开始遍历树 */
    while (cur != nullptr)/* 当当前节点不为空时，继续遍历 */
    {
        parent = cur;
        if (cur->data == value)/* 如果找到相同的值，插入失败 */
        {
            cout << "插入失败,插入的元素值不能重复" << endl;
            return false;
        }
        else if (m_comp(cur->data, value))/* 如果当前节点的值小于插入值，向右子树移动 */ 
        {
            cur = cur->right; 
        }
        else/* 否则，向左子树移动 */
        {
            cur = cur->left; 
        }
    }
    if (m_comp(value, parent->data))/* 根据比较结果，将新节点插入到父节点的左或右子树 */
    {
        parent->left = new Node(value);
    }
    else
    {
        parent->right = new Node(value);
    }
    return true;
}

3.2.2递归实现

根据上面 BST 类的定义可以看出，在进行节点递归插入的时候对 insert 函数进行了重载：

外部接口：void insert(const T& value)
内部接口：void insert(Node* root, const T& value)
因为在进行递归操作的时候，需要不停的对树中的节点进行切换，因此需要提供一个Node 类型的参数，又由于对树的操作是从根节点开始的，而我们定义的BST类的根节点是私有成员，在类外部不可见，因此在类中又提供了一个重载的外部接口insert，在外部接口insert中对内部接口insert进行调用。

点击查看代码

/* 对外的 insert 公有接口（用户调用层） */
template<typename T, typename CompFunc>
void BST<T, CompFunc>::insert(const T& value)
{
    m_root = insert(m_root, value);
}

/* 内部的 insert 递归实现（核心逻辑层） */
template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::insert(Node* root, const T& value)
{
    /* 空树：创建新节点返回（递归出口） */
    if (root == nullptr)
    {
        return new Node(value);
    }
    // 和当前节点值相同, 不允许插入
    if(root->data == value)
    {
        return root;
    }
    else if (m_comp(root->data, value))
    {
        root->right = insert(root->right, value);
    }
    else
    {
        root->left = insert(root->left, value);
    }
    return root; 
}

3.3删除操作

从二叉搜索树中删除一个值为 value 的节点。删除过程中需要处理三种不同的情况：

情况1：待删除节点没有子节点（叶子节点）。
情况2：待删除节点只有一个子节点。
情况3：待删除节点有两个子节点。

3.3.1非递归实现

点击查看代码

// bstree.hpp
template<typename T, typename CompFunc>
bool BST<T, CompFunc>::removeNormal(const T& value)
{
    // 空树
    if (m_root == nullptr)
    {
        return false;
    }
    // 搜索待删除节点
    Node* cur = m_root;
    while (cur != nullptr && cur->data != value)
    {
        if (m_comp(cur->data, value)) 
        {
            cur = cur->right;
        }
        else
        {
            cur = cur->left;
        }
    }
    if (cur == nullptr)
    {
        return false;
    }
    Node* parent = nullptr;
    if (cur->left != nullptr && cur->right != nullptr)/* 有两个子节点 */
    {
        parent = cur;/* 保存待删除节点的父节点 */
        Node* prev = cur->left;/* 查找左子树的最大节点 */
        while (prev->right != nullptr)/* 一直向右走 */
        {
            parent = prev;/* 更新父节点 */
            prev = prev->right;/* 继续向右走 */
        }
        cur->data = prev->data;/* 用最大节点的值覆盖待删除节点的值 */
        cur = prev; /* 现在删除的是最大节点 */
    }
    /*  待删节点 0/1 子 → 假设「最初的待删节点」有左子；
        待删节点 2 个子 → 假设「左子树最大节点」有左子；*/
    Node* child = cur->left;/* 先假设有左子节点 */
    if (child == nullptr)/* 左子节点为空 */
    {
        child = cur->right;
    }
    if (parent == nullptr)// 如果删除的是根节点
    {
        m_root = child;
    }
    else
    {
        if (parent->left == cur)/* 待删除节点是左子节点 */
        {
            parent->left = child;
        }
        else
        {
            parent->right = child;
        }
    }
    delete cur;
    return true;
}

在上面的示例代码中，函数的具体处理流程如下：

检查空树
- 如果树为空（m_root 为 nullptr），直接返回 false，表示删除失败。
搜索待删除节点
- 从根节点开始，使用比较函数 m_comp 查找值为 value 的节点。
- m_comp(cur->data, value) 返回 true 表示 cur->data < value，因此向右子树搜索；否则向左子树搜索。
检查是否找到待删除节点
- 如果没有找到值为 value 的节点，返回 false，表示删除失败。
处理情况3（待删除节点有两个子节点）
- 如果待删除节点有两个子节点，找到其左子树中的最大节点（前驱）或右子树中的最小节点（后继）。
- 这里选择左子树的最大节点（前驱），通过不断向右遍历左子树找到。
- 将前驱节点的值覆盖到待删除节点，然后将 cur 指向前驱节点。这样，问题转化为删除前驱节点（前驱节点最多只有一个子节点，即情况1或2）。
处理情况1或2（待删除节点有一个或没有子节点）
- 找到待删除节点的子节点（情况2）。
- - 如果左子节点存在，child 指向左子节点。
- - 如果左子节点不存在，child 指向右子节点。
- - 如果左右子节点都不存在，child 为 nullptr（情况1）。
调整父节点指针
- 如果待删除节点是根节点（parent 为 nullptr），直接将根节点指向 child。
- 否则，根据待删除节点是父节点的左子节点还是右子节点，将父节点的指针指向 child。
删除节点
- 释放待删除节点的内存。
- 返回 true，表示删除成功。

3.3.2递归实现

点击查看代码

/* 外部调用的删除节点函数 */
template<typename T, typename CompFunc>
void BST<T, CompFunc>::remove(const T& value)
{
    m_root = remove(m_root, value);
}

/* 内部递归删除节点函数 */
template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::remove(Node* root, const T& value)
{
    // 空树
    if (root == nullptr)
    {
        return nullptr;
    }
    // 找到了待删除节点
    if (root->data == value)
    {
        /* 情况 1：待删除节点有两个子节点  找到其左子树中的最大节点（前驱）或右子树中最小节点（后继） */
        if (root->left != nullptr && root->right != nullptr)
        {
            Node* prev = root->left;
            while (prev->right != nullptr)
            {
                prev = prev->right; 
            }
            root->data = prev->data;/* 用前驱节点的值覆盖待删除节点的值。 */
            root->left = remove(root->left, prev->data);/* 递归删除前驱节点。 */
        }
        else/* 情况 2 和情况 3：待删除节点有一个子节点或没有子节点 */
        {
            if (root->left != nullptr)/* 只有左子节点 */
            {
                Node* left = root->left;
                delete root;/* 删除当前节点 */
                return left;/* 返回左子节点 */
            }
            else if (root->right != nullptr)/* 只有右子节点 */
            {
                Node* right = root->right;
                delete root;/* 删除当前节点 */
                return right;/* 返回右子节点 */
            }
            else/* 没有子节点 */
            {
                delete root;/* 删除当前节点 */
                return nullptr;/* 返回空指针 */
            }
        }
    }
    else if (m_comp(root->data, value))/* 如果当前节点的值小于 value，递归查找右子树。 */
    {
        root->right = remove(root->right, value); 
    }
    else/* 如果当前节点的值大于 value，递归查找左子树。 */
    {
        root->left = remove(root->left, value);
    }
    return root;
}

3.4查找操作

3.4.1非递归实现

遍历树

3.4.2递归实现

点击查看代码

// bstree.hpp
template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::query(const T& value)
{
    return query(m_root, value);
}

template<typename T, typename CompFunc>
typename BST<T, CompFunc>::Node* BST<T, CompFunc>::query(Node* root, const T& value)
{
    // 空树
    if (root == nullptr)
    {
        return nullptr;
    }
    if (root->data == value)
    {
        return root;    // 找到了
    }
    else if (m_comp(root->data, value))
    {
        return query(root->right, value);
    }
    else
    {
        return query(root->left, value);
    }
}

3.5中序遍历

posted @ 2026-01-06 14:49 r5ett 阅读(3) 评论(0) 收藏举报

刷新页面返回顶部

r5ett

3.二叉搜索树

1.二叉搜索树概述

2.二叉搜索树的基本操作

2.1查找操作

2.2插入操作

2.3删除操作

3.二叉搜索树的实现

3.1构造和析构

3.1.1构造函数

3.1.2析构函数

3.2插入操作

3.2.1非递归实现

3.2.2递归实现

3.3删除操作

3.3.1非递归实现

3.3.2递归实现

3.4查找操作

3.4.1非递归实现

3.4.2递归实现

3.5中序遍历

公告