2.二叉树以及它的形态、性质、存储结构和遍历

1.二叉树

二叉树是一种树形数据结构，其中每个节点最多有两个子节点（0，1，2），分别称为‌左子节点和‌右子节点。二叉树由一个根节点和两棵互不相交的子树组成，这两棵子树分别称为根的左子树和右子树。二叉树的定义可以递归地描述：二叉树是一个有限的节点集合，这个集合可以是空集（即没有节点），或者由一个根节点和两棵互不相交的二叉树组成。‌
image

1.1二叉树的特点和形态

二叉树有三个特点依次是：

  • 每个节点最多有两棵子树，所以二叉树中不存在度大于2的节点
  • 左子树和右子树是有顺序的，次序不能颠倒，也就是说二叉树是有序树
  • 即使树中某节点只有一棵子树，也要区分它是左子树还是右子树

基于以上描述，我们对二叉树的形态做了归纳，一共有五种形态，分别是：

  • 空二叉树
  • 只有一个根节点
  • 根节点只有左子树
  • 根节点只有右子树
  • 根节点既有左子树，又有右子树

1.2特殊的二叉树

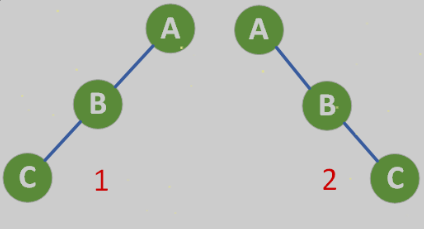
斜树
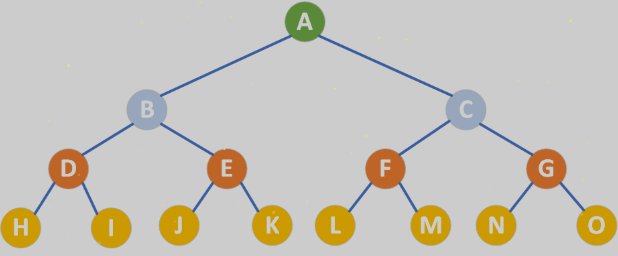
image
满二叉树
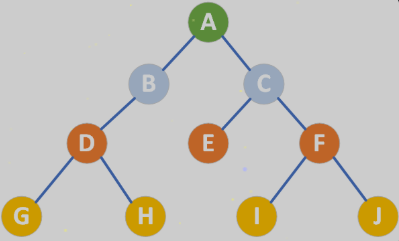
image
完全二叉树
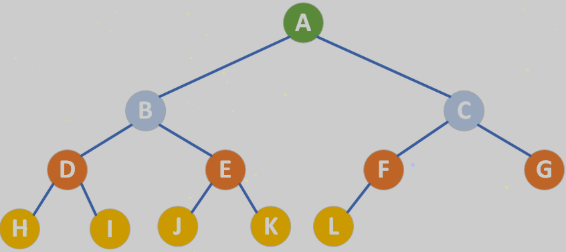
image

2.二叉树的性质

image

  • 性质1：二叉树的第 i 层上至多有 2i-1（i≥1）个节点 。
  • 性质2：深度为 k 的二叉树中至多含有 2k-1 个节点（k≥1） 。
  • 性质3：若在任意一棵二叉树中，叶子节点有 n0 个，度为2的节点有 n2个，则 n0=n2+1 。
  • 性质4：具有n个节点的完全二叉树的深度为 ⌊log2n⌋+1（⌊ ⌋ 表示向下取整）。
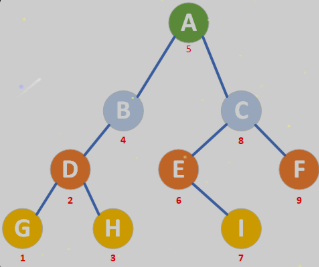
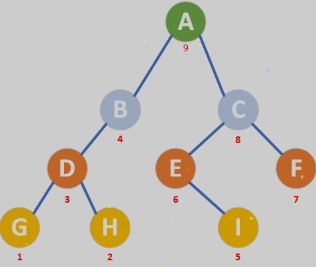
  • 性质5：若对一棵有 n 个节点的完全二叉树的节点按层序进行编号（从第1层到第 ⌊log2n⌋+1层，每层从左到右），那么，对于编号为i（1≤i≤n）的节点：

（1）当i=1时，该节点为根，它无双亲节点 。
（2）当i>1时，该节点的双亲节点的编号为i/2 。

  • 对于上图而言，编号为7(G)的节点，其父节点为 3(C)
  • 对于上图而言，编号为5(E)的节点，其父节点为 2(B)
  • 对于上图而言，编号为11(K)的节点，其父节点为 5(E)

（3）若2i≤n，则有编号为2i的左节点，否则没有左节点 。

  • 上图中的G(7)、H(8)、I(9)、J(10)、K(11)、L(12) 乘以2 > n(12)，它们没有左节点
  • 上图中的A(1)、B(2)、C(3)、D(4)、E(5)、F(6) 乘以2 ≤ n(12)，它们有左节点

（4）若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点。

  • 上图中的节点F，2*(F)+1 = 13 > n(12)，它没有右节点
  • 上图中的A(1)、B(2)、C(3)、D(4)、E(5) 乘以2 + 1 < n(12)，它们有右节点

3.二叉树的存储结构

3.1顺序存储

二叉树的顺序存储结构就是用一维数组存储二叉树中的节点，并且通过数组的下标来描述节点之间的逻辑关系，比如双亲和孩子的关系，左右兄弟的关系等。
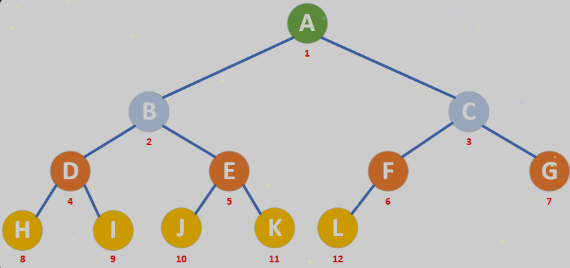
image
如果从数组的1号位置开始存储数据，二叉树的节点在数组的位置应该是这样的：
image
如果从数组的0号位置开始存储数据，二叉树的节点在数组的位置应该是这样的：
image
如果存储的二叉树不是完全二叉树，此时在数组中应该如何存储二叉树的节点呢？
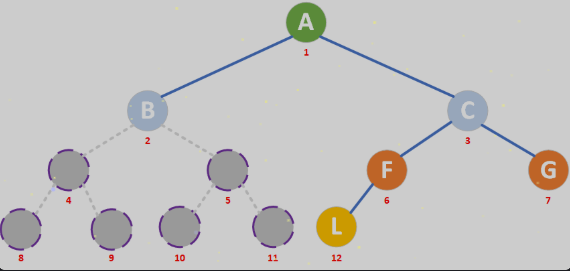
image
在上面这棵二叉树中有很多节点缺失了，为了看起来更直观，我们使用灰色将其画了出来，使用完全二叉树的方式来存储这棵普通的二叉树数据
image
通过上面的表可以清晰的看到使用顺序存储的方式存储二叉树会造成内存的浪费，尤其是当二叉树变成一棵右斜树的时候，浪费的内存空间是最多的。所以顺序存储结构一般只用于存储完全二叉树。

3.2链式存储

既然顺序存储结果有弊端，我们在来看一下链式存储结果能不能弥补这个缺陷。由于二叉树每个节点最多只有两个孩子，所以为每个树节点设计一个数据域和两个指针域，通过这种方式组成的链表我们称其为二叉链表。

struct TreeNode
{
    int data;
    TreeNode* lchild;
    TreeNode* rchild;
};
  • data：存储节点数据，可以根据实际需求指定它的类型。
  • lchild：存储左侧孩子节点的地址。
  • rchild：存储右侧孩子节点的地址.
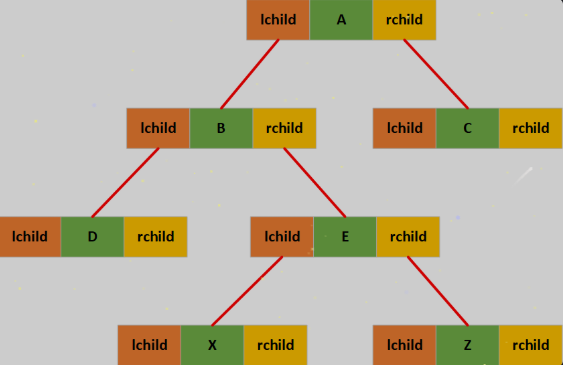
    image
    但是想要通过孩子节点访问父节点就比较麻烦了，解决方案也比较简单我们可以给链表节点再添加一个指针域，让它指向当前节点的父节点：
struct TreeNode
{
    int data;
    TreeNode* lchild;
    TreeNode* rchild;
    TreeNode* parent;
};
  • parent：存储双亲节点（父节点）的地址。

4.二叉树的遍历

二叉树的遍历是指从根节点出发，按照某种次序依次访问二叉树中的所有节点，使得每个节点被访问一次并且仅被访问一次。
通过递归的方式对树进行遍历一共有三种方式：

  • 前序遍历：先访问根节点，然后前序遍历左子树，最后前序遍历右子树
  • 中序遍历：中序遍历左子树，然后访问根节点，最后中序遍历右子树
  • 后序遍历：后序遍历左子树，然后后序遍历右子树，最后访问根节点
    通过三种遍历方式的定义可知，前、中、后其实是相对于根节点而言的，并且二叉树的左子树和右子树的遍历也是递归的，同样遵循前序、中序、后序的规则，在遍历过程中如果树为空，直接返回，递归结束。

4.1前序遍历

4.1.1递归实现

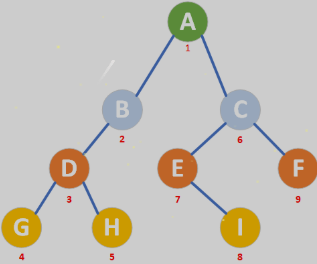
image

// 前序递归遍历函数
void preorder(TreeNode* root) 
{
    if (root == nullptr) 
    {
        return;
    }
    cout << root->val << " ";
    preorder(root->left);
    preorder(root->right);
}
  • 首先检查当前节点是否为空，如果为空则直接返回，这是递归的终止条件。
  • 若节点不为空，先输出该节点的值，完成对根节点的访问。
  • 然后递归调用 preorder 函数处理左子树。
  • 最后递归调用 preorder 函数处理右子树。

4.1.2非递归实现

关于二叉树的遍历除了使用递归方式，还可以使用非递归方式。我们可以借助栈来完成这个操作，具体步骤如下：

  • 初始化：若树为空，直接结束；否则，将根节点压入栈。
  • 遍历过程（当栈不为空时，重复以下操作）：
    • 弹出栈顶节点并访问它。
    • 若该节点的右子节点不为空，将右子节点压入栈。
    • 若该节点的左子节点不为空，将左子节点压入栈。
  • 终止条件：当栈为空时，遍历结束。
    因为栈是后进先出的结构，所以先压入右子节点，再压入左子节点，就能保证左子节点先被访问。

4.2中序遍历

4.2.1递归实现

image

// 中序递归遍历函数
void inorder(TreeNode* root) 
{
    if (root == nullptr) 
    {
        return;
    }
    inorder(root->left);
    cout << root->val << " ";
    inorder(root->right);
}
  • 首先判断当前节点是否为空，若为空则直接返回，这是递归的终止条件。
  • 递归调用 inorder 函数处理左子树。
  • 输出当前节点的值，完成对根节点的访问。
  • 递归调用 inorder 函数处理右子树。

4.2.2非递归实现

通过非递归的方式实现二叉树的中序遍历，还是需要借助数据结构中的栈。遍历的具体步骤如下：

  • 初始化
    • 若树为空，直接结束。
    • 创建一个空栈，并让辅助指针 current 指向根节点。
  • 循环处理（current 不为空或栈不为空）：
    • 左子树入栈：将 current 的所有左子节点依次压入栈，直到 current 为空。
    • 弹出并访问：弹出栈顶节点，访问该节点。
    • 转向右子树：将 current 指向弹出节点的右子节点。
void inorderTraversal(TreeNode* root) 
{
    stack<TreeNode*> nodeStack;
    TreeNode* current = root;
    // 当当前节点不为空或栈不为空时继续遍历
    while (current != nullptr || !nodeStack.empty()) 
    {
        // 遍历到最左节点，将路径上的节点压入栈中
        while (current != nullptr) 
        {
            nodeStack.push(current);/* 把节点指针压入栈顶 */
            current = current->left;
        }

        // 从栈中弹出节点并访问
        current = nodeStack.top();/* 获取栈顶元素（只读取，不移除）*/
        nodeStack.pop();/* 移除栈顶元素 */
        cout << current->val << " ";
        // 转向右子树
        current = current->right;
    }
}

4.3后续遍历

4.3.1递归实现

image

void postorder(TreeNode* root)
{
    if (root == nullptr)
    {
        return;
    }
    postorder(root->left);
    postorder(root->right);
    cout << root->val << " ";
}
  • 首先判断当前节点是否为空，若为空则直接返回，这是递归的终止条件。
  • 递归调用 postorder 函数处理左子树。
  • 递归调用 postorder 函数处理右子树。
  • 输出当前节点的值，完成对根节点的访问。

4.3.2非递归实现

通过非递归的方式实现二叉树的后序遍历，可以使用单栈标记法也可以使用双栈法。
这里用双栈法，其核心思想如下：

  • 用 栈1 按 根 → 左 → 右 顺序压入节点。
  • 将 栈1 弹出的节点压入 栈2，最终 栈2 的出栈顺序即为 左 → 右 → 根（后序）。
    具体步骤：
  • 根节点压入栈1。
  • 循环弹出栈1，依次压入其左子节点、右子节点到栈1。
  • 将弹出的节点压入栈2。
  • 最终依次弹出栈2的节点并访问。
void postorderTraversal(TreeNode* root) 
{
    if (!root) return;
    stack<TreeNode*> stack1, stack2;
    stack1.push(root);

    while (!stack1.empty()) 
    {
        TreeNode* node = stack1.top();/* 获取第一个栈的顶部节点 */
        stack1.pop();/* 弹出第一个栈的顶部节点 */
        stack2.push(node);/* 将当前节点压入第二个栈 */

        if (node->left)
        {
            stack1.push(node->left);
        }
        if (node->right) 
        {
            stack1.push(node->right);
        }
    }

    while (!stack2.empty()) 
    {
        cout << stack2.top()->val << " ";
        stack2.pop();
    }
}

4.4层序遍历

二叉树的层序遍历是一种广度优先搜索（BFS）的应用，它按照从上到下、从左到右的顺序依次访问二叉树中的每个节点。层序遍历在很多实际场景中都有应用，比如按层处理树状结构的数据、计算树的宽度等。
层序遍历通常借助队列（先进先出）这一数据结构来实现。具体步骤如下：

  • 初始化：创建一个队列，并将根节点入队列。
  • 循环处理：当队列不为空时，执行以下操作：
    • 从队列中取出一个节点。
    • 访问该节点（比如打印节点的值）。
    • 如果该节点有左子节点，将左子节点入队列。
    • 如果该节点有右子节点，将右子节点入队列。
  • 结束条件：当队列为空时，遍历结束。
void levelOrder(TreeNode* root) 
{
    if (root == nullptr) return;
    queue<TreeNode*> q;
    q.push(root);

    while (!q.empty()) 
    {
        int levelSize = q.size();/* 获取当前层的节点数 */
        // 处理当前层的所有节点
        for (int i = 0; i < levelSize; ++i) 
        {
            TreeNode* current = q.front();/* 获取当前节点 */
            q.pop();/* 弹出队列 */
            cout << current->val << " ";

            // 将当前节点的左右子节点入队
            if (current->left)
            {
                q.push(current->left);
            }
            if (current->right)
            {
                q.push(current->right);
            }
        }
        cout << endl;
    }
}

5.二叉树的创建

5.1直接构建二叉树

想要构建一棵二叉树最简单的方式就是创建若干个节点，然后按照父子、兄弟关系把它们通过指针连接到一起，这种创建二叉树的方法特点是简单，但是不够灵活。

5.2通过终端输入构建二叉树

如果想要灵活地创建出一个二叉树，可以让用户通过终端输入的方式指定出节点的值以及节点和节点之间的关系，但是有一个细节需要进行处理，就是某些节点没有左孩子或者右孩子。因此，我们可以做这样的一个约定：如果节点的左孩子或者右孩子为空，那么在输入的时候就使用 # 来表示。
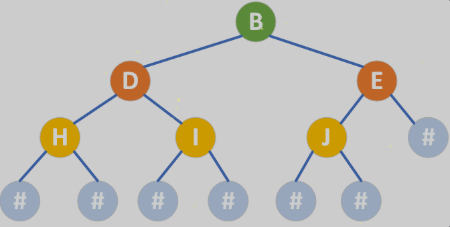
image
就是用cin手动输入

5.3释放树节点

因为在上面的代码中二叉树的节点是动态创建的，所以在程序的最后还需要释放节点资源，关于释放的顺序应该是先释放子节点然后释放父节点，所以对应的遍历方式应该是后序遍历。

posted @ 2026-01-06 14:49  r5ett  阅读(15)  评论(0)    收藏  举报